Хотелось бы в самом начале обобщить главные аспекты ниже приведенного материала. Работа Л.Б. Борисова рассматривает такие аспекты, как искривление пространства-времени Общей теории относительности, римановы пространства для описания искривления четырехмерного пространства, а также перехода от трехмерности к многомерности. О том, что осознание времени как измерения – путь к выходу из трёхмерного плена, одномерное время – лишь первый шаг к осознанию многомерности, условиях, при которых физически наблюдаемое время останавливается. Ниже приведены фрагмент его работы с вычетов нечитабельных формул для широкого круга читателей. Сразу приведу ссылку на работу, всем кому будет интересно читать полную версию, пожалуйста: http://www.delphis.ru/journal/article/prostranstvo-vremya-ka...

О взаимодействии жидкой среды и физического вакуума.

Существуют такие трёхмерные пространства метрик, которые обладают постоянными положительными трёхмерными кривизнами. Кривизна пространства-времени может быть отрицательна. Однако пространство-время некоторых метрик не обладает постоянной кривизной. Поскольку некоторые величины в гравитационных полях, созданных жидкой сферой и вакуумным пузырём, имеют противоположные знаки, можно утверждать: сила притяжения обусловлена положительной, а сила отталкивания – отрицательной «кривизной времени». Таким образом, при определенном условии (b=[3/(κρ)]½=(3/λ)½), эквивалентном условию κρ=3/а2, мгновенно 

* несжимаемая жидкость трансформируется в физический вакуум в состоянии инфляции

* гравитационное притяжение превращается в отталкивание; 

* «кривизна времени» меняет знак. 

Кроме того, (при r=а) вакуумный пузырь 

* превращается в инфляционный коллапсар

* испытывает разрыв пространства. 

Фактически жидкая сфера «выворачивается» во времени наизнанку, где «изнанкой» является инфляционный вакуум. Это выворачивание эквивалентно переходу с одной стороны трёхмерной поверхности Мёбиуса на другую при условии, что ход времени на одной из сторон противоположен ходу времени на другой. Это означает, что базисные векторы e0 на каждой из сторон имеют противоположные направления. Пространства с прямым (dτ>0) и обратным (dτ<0) ходом наблюдаемого времени (пространства прошлого и будущего) совпадают на гиперповерхности dτ=0 (пространство настоящего), где длины обоих векторов нулевые (e0=0). Таким образом, физически наблюдаемое время подобно ленте Мёбиуса. 

Время воспринимается сознанием как одномерное и направленное из прошлого в будущее. Между тем повторяемость в разные эпохи схожих по энергетике событий свидетельствует в пользу того, что прошлое и будущее зеркальны по отношению друг к другу, а зеркалом является настоящее. 

Взято из статьи Л.Б. Борисова, кандидата физико-математических наук. Ссылка на полную статью: http://www.delphis.ru/journal/article/prostranstvo-vremya-ka...

Основной задачей этой и предыдущих двух работ было показать связанность различных мелких аспектов строения жизни на таком примере, как петля Мёбиуса, которые могут рассматриваться в разных отраслях науки. 

Спасибо за внимание.

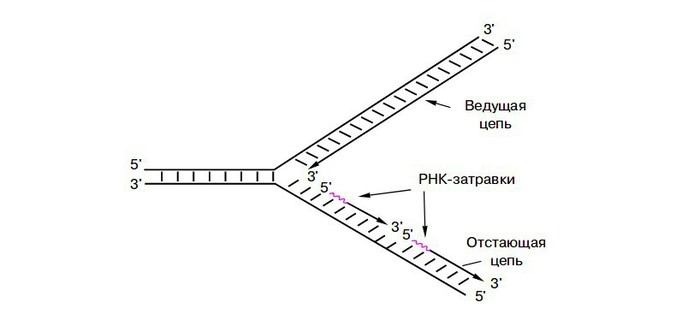
Все мы на уровне понимания знаем, что такое ДНК, но сегодня хотелось бы капнуть чуть глубже. Как вы уже знаете ДНК представляет собой двойную спираль, закрученную антипараллельно и идущую в разных направлениях. Это значит, что одна нить идет в направлении от 5' конца к 3', а комплементарная ей — наоборот. Цифры 5 и 3 обозначают номера атомов углерода в дезоксирибозе, входящей в состав каждого нуклеотида. 

Репликация ДНК — это процесс ее удвоения перед делением клетки. Удвоение происходит в S-фазе интерфазы клеточного цикла. Удвоение интересно тем, что происходит формирование репликационных вилок. При этом на одной материнской цепи синтез идет в сторону расхождения вилки, и этот синтез происходить непрерывно, без разрывов. На второй матрице синтез идет в обратную сторону от направления расхождения цепей исходной ДНК. Поэтому такой обратный синтез может идти только кусками, которые называются фрагментами Оказаки. Позже такие фрагменты «сшиваются» между собой. 

Как только было доказано, что ДНК может быть кольцевой, ДНК бактерий, плазмидов - кольцевые, а также, что кольцевая форма ДНК чрезвычайно распространена, то возник вопрос о топологии ДНК. Тогда появилось новая область изучения на стыке математики, биофизики, биохимии, биологии и медицины - топология ДНК. Как уже говорилось, двойная спираль ДНК закручена, и с точки зрения математики к проблемам раскручивания ДНК применима теория узлов. Теория узлов была прекрасно развита для целого ряда инженерных специальностей, профессор Франк-Каменецкий был одним из лидеров этого направления в 70–80-е годы. Ныне он работает в университете Бостона. Тем не менее это были основополагающие работы, прекрасно цитируемые.

Интерес к топологии ДНК был также у математиков из Института теоретической и экспериментальной физики, в частности у профессора Монастырского — очень известного тополога, который и модифицировал некоторые уравнения, применимые для замкнутой ленты — а ДНК рассматривалась именно как замкнутая лента, — и предложил механизмы разрыва ребер ленты. Это легло в основу целого направления дальнейших исследований ДНК, потому что экспериментально разрывы в молекуле ДНК можно наблюдать с помощью метода линейного дихроизма.

Рассмотрение ДНК с точки зрения замкнутых линий возвращает нас к петле Мёбиуса. То есть, когда ДНК сильно перекручено, допустим 3 раза, и начинается процесс репликации, ДНК начинает раздваиваться. А так как она имеет форму поверхности Мёбиуса, то это нас приводит к образованию узлов молекулы - вспомните из первой части пример с разрезанием трижды перекрученной ленты. Могут возникать не только узлы, а также более длинные петли, соединенные петли и т.д. Что бы развязать узел, надо сделать определенное количество перецеплений, то есть разорвать молекулу ДНК и сшить её потом обратно. В клетке существует механизм, препятствующий образованию узлов. Существует большой класс ферментов, названные Топоизомеразы, к примеру два топологических изомера - узел и не узел. Эти ферменты умеют завязывать и развязывать узлы. Топоизомераза типа 2 разрывает обе цепочки молекулы ДНК и пропускает через брешь остальную часть ДНК, а потом сшивает молекулу. Это очень сложный процесс, изученный с помощью рентгеноструктурного анализа на атомном уровне. Двухнитевой разрыв для ДНК - это смерть в клетке, так как разрывы подобного рода не репарируются. Воздействовав определенным образом на эти топоизомеразы, можно предотвратить развития раковых клеток как раз путём разрыва топологических участков ДНК. Теперь ясно, что надо искать именно те молекулы, которые воздействуют на топоизомеразы. 

Полезные источники:

https://www.youtube.com/watch?v=oQtKIPGhENs

https://postnauka.ru/video/36239

Спасибо за внимание.

Уже не первый раз встречается такое явление в истории, что два учёных делают новые открытия одновременно и независимо друг от друга. Так и произошло в 1858 г., когда математики: Август Фердинанд Мёбиус и Иоганн Бенедикт Листинг открыли ленту Мёбиуса.

 Её также называют петлёй, листом или поверхностью. Эта петля является топологической, то есть непрерывным объектом с простейшей односторонней поверхностью с границей в обычном Евклидовом пространстве R^3, где возможно из одной точки такой поверхности, не пересекая края, попасть в любую другую. Топология - раздел математики, изучающий в общем виде непрерывность, в частности свойства пространства, которые остаются неизменными при непрерывных деформациях. В отличие от геометрии, в топологии не рассматриваются метрические свойства объектов. Эта лента вызывает такой интерес именно потому, что у нее всего одна сторона, а её граница состоит из одной замкнутой кривой. 

 До 1858 г. считалось, что любая поверхность обязана быть двухсторонней. Лента была названа в честь Мёбиуса, т.к. он в своём труде «Об объёме многогранников» описал её геометрическую поверхность. Листинг считается отцом основателем топологии. 

Одним из интересных свойств этой поверхности является то, что лента является двухмерным объектом, который можно полностью показать только в трехмерном пространстве, а так же, если вы начнёте чертить линию вдоль центра петли, в конечном итоге траектория замкнётся и вы придете туда, откуда начали. Это не сложно проверить, взяв квадрат или прямоугольник и соединив его стороны, перекрутив их при этом. Лучшую вещь, которую вы сейчас можете с ней сделать - это разрезать вдоль её центра. Отличие заключается в том, что, разрезав любую другую фигуру вдоль центра, вы получите две фигуры. Разрезав поверхность Мёбиуса такого не произойдет. У вас будет всё та же петля, только другой длинны и ширины. Если вы возьмете и трижды перекрутите кольцо (когда вы делали эту петлю, вы перекручивали один раз), то вы получите трижды перекрученную ленту Мёбиуса. Кстати, она же по совместительству является логом компании по переработки мусора. Интерес заключается в том, что, попытавшись разрезать ленту вдоль её центра теперь, вы получаете снова петлю Мёбиуса, только теперь с образовавшимся на ней узлом. Интерес этот случай вызывает в биологии при репликации участков молекулы ДНК и образование на ней узлов. 

Спасибо за внимание.

В детстве мне попалась в руки книга американского математика Мартина Гарднера "математические доуги", которую я, имея скорее гуманитарный склад ума, всё же с интересом читал. Там был описан интересный опыт разрезания этой ленты вдоль. Я решил сделать такую ленту и проверить, что получается

Сделал из широкой изоленты, разрезал

И получил, как и было описано - вдвое более длинную, дважды перекрученную ленту Мёбиуса!

И тут мой гуманитарный мозг осенила идея. А что получится, если её разрезать еще раз ?
Никаких причин откладывать  у меня не было, и я это сделал.

Внимание, вопрос) У кого какие мысли, что у меня получилось?
Результат меня удивил, не скрою, ответ дам чуть позже)