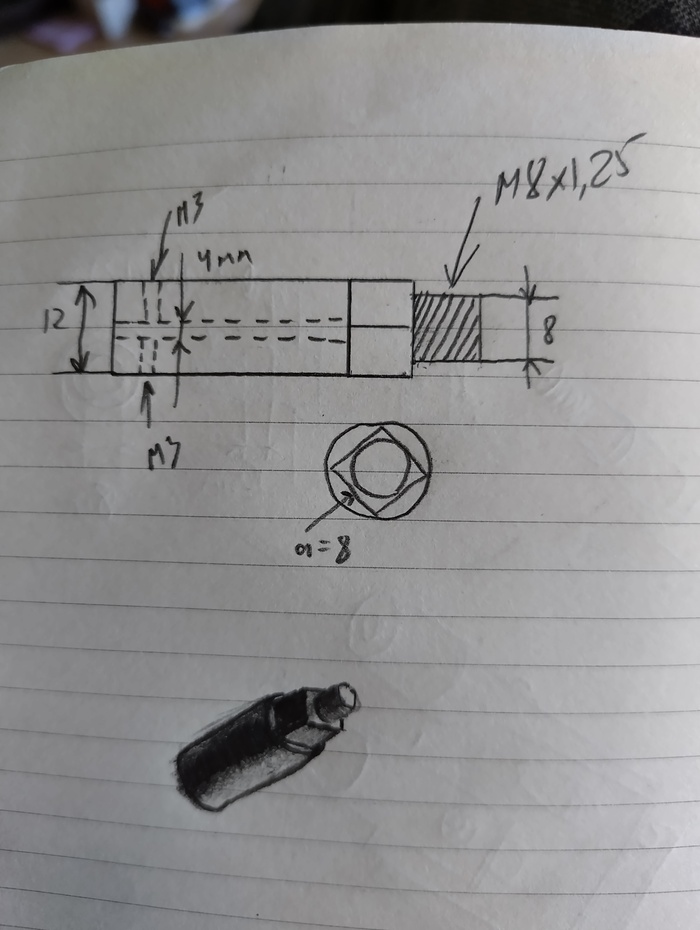
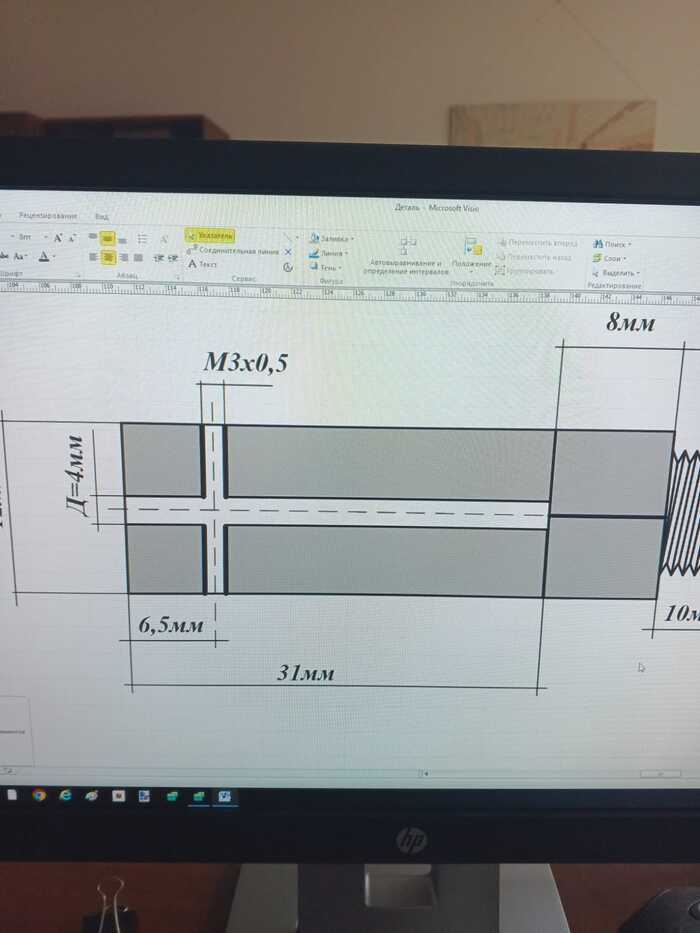
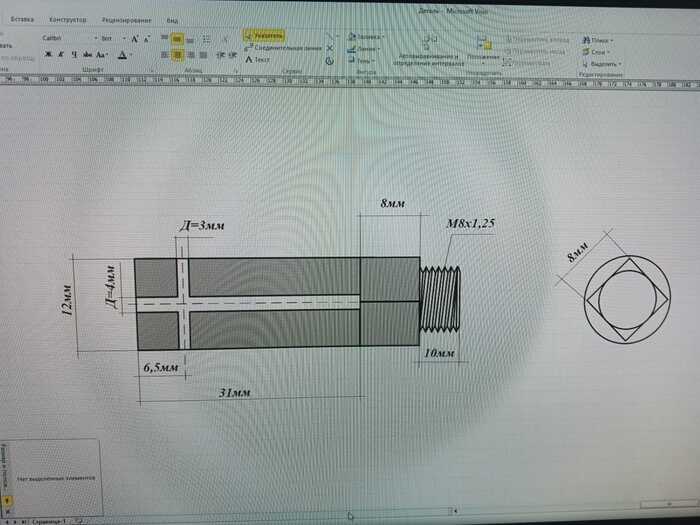
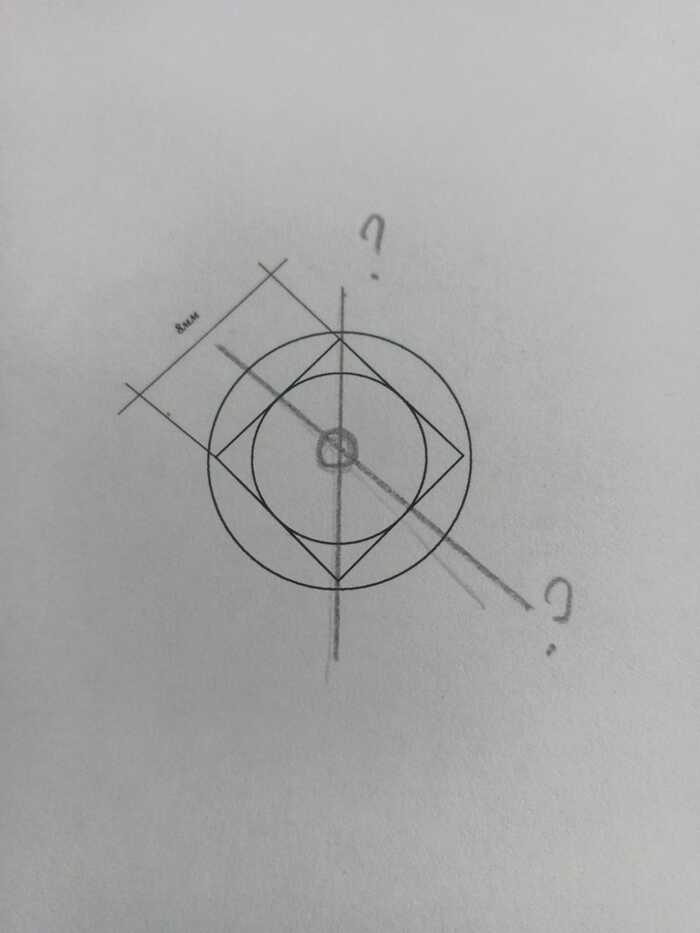
(В первом посте не будет описан сам процесс изготовления астротрекера, а только лишь теория. Будем считать секунды. И да - это не проектная документация с идеальными расчетами, а моя история создания сего девайса, не без огрехов.)
(@Scaletto, я сделяль! И не забыл, что один человек подписался ради этой штуки.)
Для тех, кто еще не понял, о чём пойдет речь - штукенция называется Barn Door Tracker. Позволяет делать фото звёзд на длинной выдержке. Самое простое приспособление для этой цели.
Масштаб трагедии
Давным-давно, один любитель астрономии захотел сфотографировать далекую-далекую галактику. Но вот беда - на длинной выдержке изображения звёзд получаются вытянутыми. Всему виной вращение купола над плоскостью Земли нашей планеты вокруг своей оси.
Если вы ни разу не пробовали фотографировать звёзды, то масштаб трагедии можно оценить на следующем фото:
Снято на Nikon D5300 (и далее только эта тушка), Sigma 17-50 f/2.8, 34mm, 30 sec, f/3.5, ISO 200. Восточная область неба. Красная зона засветки.
Главное здесь это выдержка и эквивалентное фокусное расстояние. Чем больше эти два параметра, тем длиннее треки звёзд. На самом деле, нужно учитывать и размер пикселя, но камера у меня одна.
Если уж совсем дотошно (а иначе тут нельзя), то одним из факторов нужно назвать участок неба, который фотографируется. Чем ближе он к полюсу мира, тем меньший путь проделывает звезда по кадру.
На картинке выше (программа Stellarium) изображена область Северного полюса мира. И да, он находится не точно на Полярной звезде. Более того, ПМ смещается из-за прецессии земной оси. К счастью, нам этот фактор особо учитывать не придется :)
Так вот. Здесь мы видим условные линии-окружности (т.н. экваториальная сетка). По ним и двигаются звёзды. И чем дальше точка находится от ПМ, тем больше длина этой окружности. Однако же, угловая скорость у них у всех одинаковая.
E pur si muove!
Итого: чтобы получить фото неба со звёздами в виде точек, а не треков, нужно компенсировать вращение Земли. Давайте разбираться.
Все мы знаем, что сутки равняются 24-м часам. Но это солнечные сутки. Нас же интересуют звёздные сутки. Это именно то время, за которое Земля делает полный оборот относительно далёких звёзд, а не Солнца.
Звёздные сутки на 2000-й год равняются 86164,090530833 секундам. На 2003-й по данным IERS - 86164,098903691 секунд. Разница не велика и не существенна. Более свежих данных на скорую руку не нашел. Да и ладно. Но если у кого-то есть ссылка - прошу поделиться.
ЗС - 23 часа 56 минут 4 секунды. Отклонение от солнечных суток в несколько минут это и есть причина, по которой вводится один день в високосный год и високосные секунды.
Вернемся к расчетам. Период обращения планеты вокруг своей оси мы высчитали нагуглили. Нужно посчитать скорость. Это не сложно. Полный оборот это 360 градусов.
360 / 86164,098903691 = 0,004178074216297 градуса в секунду.
Тысячными долями градуса не так удобно оперировать. Давайте переведём всё в угловые секунды. Здесь тоже ничего сложного - в одном градусе 60 угловых минут. В одной угловой минуте 60 угловых секунд.
0,004178074216297 * 3600 = 15,0410671786702 угловых секунд (ArcSec - "секунда дуги") в секунду времени.
Вот мы и узнали "скорость движения звёзд по небу".
Секунды, секунды, секунды...
А ведь увлекательное это занятие - считать секунды. Я начинаю понимать некоторых личностей...
Следующим шагом мы вычислим требуемую точность. Оценим необходимую погрешность для поставленной цели-минимум. Для себя решил, что проект можно будет считать успешным при достижении выдержки в 30 секунд на объективе с ФР 50 мм. Совсем скромная цель, но давайте для начала посчитаем, какая минимальная выдержка может быть на таком ФР без трекера.
Скорость движения звёзд по небу нам уже известна. Осталось разобраться с камерой. В моём девайсе матрица кропнутая (кроп-фактор 1,5; 23,5 мм х 15,6 мм) и разрешение - 6000х4000.
Воспользуемся специальным калькулятором. По нашим параметрам имеем:
Ширина кадра: 1615,86 угловых минут
Высота кадра: 1065,78 угловых минут
На один пиксель приходится 16,1586 угловых секунд.
Для простоты расчетов предположим, что звезда двигается по прямой, а не по окружности. Это очень грубый расчет, но он позволит хотя бы примерно представить, чего нужно достичь. В теории, такой расчет близко применим для звёзд, находящихся на линии небесного экватора. Могу ошибаться. Поправьте, если не так.
15,0410671786702 / 16,1586 = 0,931 пикселей в секунду.
Почти один пиксель в секунду проходит звезда по кадру! Это означает, что выдержка в 2 секунды уже будет с вытянутой звездой. Конечно, огрехи оптики, атмосфера, сам факт накопления сигнала и прочие факторы не позволят увидеть звезду-пиксель даже при выдержке в 1/2 секунды. Но оно нам и не надо.
В пейзажном астрофото есть "правило 600" (иногда "правило 500"):
600 / (ФР * кроп-фактор) = оптимальная выдержка
Считается, что кадр, снятый с соблюдением этого правила выглядит хорошо, без треков.
600 / (50 * 1,5) = 8 секунд
За 8 секунд по "идеальному расчету" звезды размажутся на ~7,5 пикселей. И это считается нормой. Ну ок. Мне самому не особо нравится такой расклад.
Вот такая занятная табличка получается по расчетам. Отклонение в пикселях, ФР без учета кропа.
Для будущих тестов у меня имеется уже упомянутый объектив 17-50 мм, 135 мм и 300 мм.
На этом моя первая часть - всё.
В следующем посте покажу расчеты параметров трекера, используемые материалы и схему устройства.