Алгоритмы поиска в гошечке (golang)
Привет, чувачёчки.
В этом посте я хочу поделиться с вами кодом на Go для некоторых популярных алгоритмов поиска.
Наслаждайтесь.
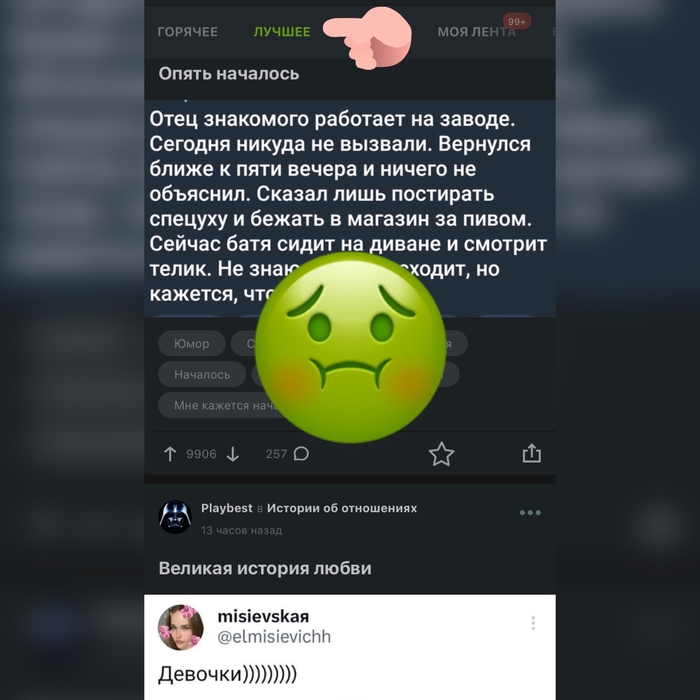
Линейный поиск
Линейный поиск (Linear Search) - это простой алгоритм поиска элемента в списке, массиве или коллекции. Он работает путем последовательного перебора всех элементов до тех пор, пока не будет найден искомый элемент или не будут проверены все элементы.
Описание алгоритма:
1. Начните с первого элемента списка.
2. Сравните его с искомым элементом.
3. Если элемент совпадает с искомым, верните его индекс (или значение, в зависимости от реализации).
4. Если элемент не совпадает с искомым, перейдите к следующему элементу в списке.
5. Повторяйте шаги 2-4 до тех пор, пока не найдете искомый элемент или не пройдете весь список.
Линейный поиск имеет временную сложность O(n), где "n" - это количество элементов в списке. В худшем случае алгоритм может проверить все элементы, поэтому его производительность ухудшается с ростом размера списка.
Помимо своей простоты, линейный поиск также может применяться в неотсортированных списках или там, где нет возможности использовать более сложные алгоритмы поиска, такие как двоичный поиск. Однако для больших объемов данных и поиска в отсортированных структурах обычно рекомендуется использовать более эффективные алгоритмы.
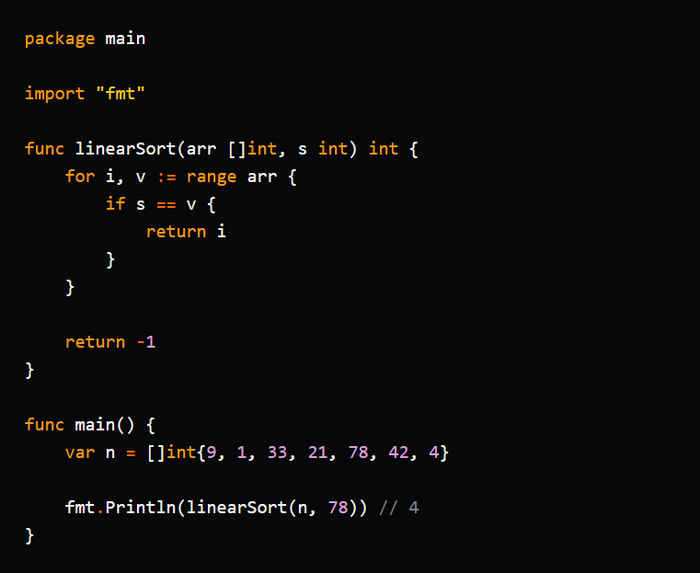
Бинарный поиск
Бинарный поиск (Binary Search) - это эффективный алгоритм поиска элемента в отсортированном списке, массиве или коллекции. Он использует стратегию "разделяй и властвуй", что позволяет быстро находить искомый элемент.
Описание алгоритма:
1. Начните с определения границ поиска. Установите начальную границу (left) в начало списка и конечную границу (right) в его конец.
2. Найдите средний элемент между начальной и конечной границей.
3. Сравните средний элемент с искомым значением.
4. Если средний элемент совпадает с искомым значением, возвращаем его индекс (или значение, в зависимости от реализации).
5. Если средний элемент больше искомого значения, обновите конечную границу (right) на позицию перед средним элементом и перейдите к шагу 2.
6. Если средний элемент меньше искомого значения, обновите начальную границу (left) на позицию после среднего элемента и перейдите к шагу 2.
7. Повторяйте шаги 2-6 до тех пор, пока не будет найден искомый элемент или пока начальная граница (left) не станет больше конечной границы (right).
Бинарный поиск имеет временную сложность O(log n), где "n" - это количество элементов в списке. Это означает, что в худшем случае алгоритм будет выполняться за логарифмическое время, что является значительно более эффективным, чем линейный поиск.
Однако для применения бинарного поиска список должен быть отсортирован по возрастанию или убыванию. В противном случае результаты будут непредсказуемыми. Бинарный поиск особенно полезен, когда требуется повторно выполнять поиск в отсортированных структурах данных, таких как массивы или списки, с минимальными затратами на время выполнения.
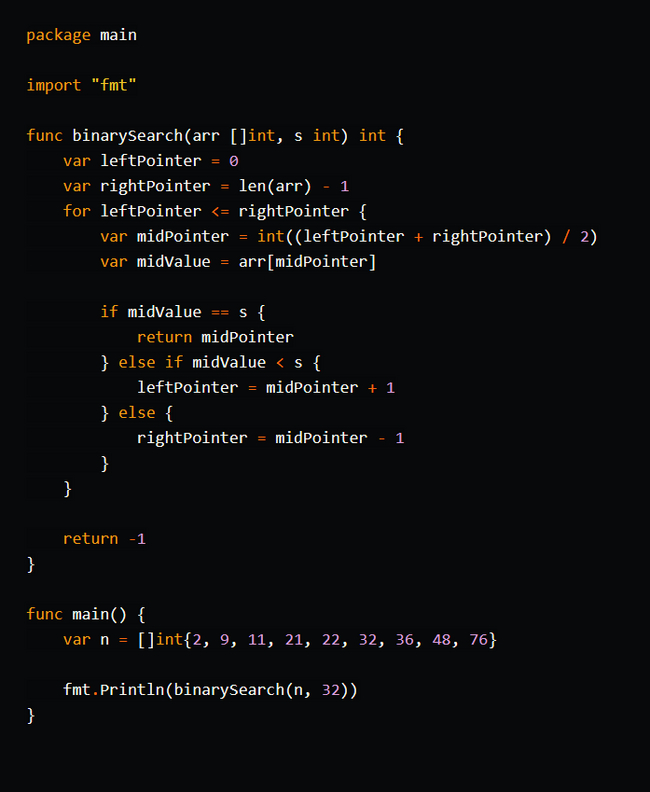
Прыжковый поиск
Прыжковый поиск (Jump Search) - это алгоритм поиска элемента в отсортированном списке, массиве или коллекции. Он использует идею деления интервала на блоки и прыжки через эти блоки для быстрого приближения к искомому элементу.
Описание алгоритма:
1. Задайте размер прыжка (jump size). Обычно он выбирается как квадратный корень из общего количества элементов в списке.
2. Начните с первого элемента списка.
3. Сравните текущий элемент с искомым значением.
4. Если текущий элемент равен искомому значению, верните его индекс (или значение, в зависимости от реализации).
5. Если текущий элемент больше искомого значения или достигнут конец списка, перейдите к следующему шагу.
6. Сделайте прыжок через блоки, перемещаясь вперед на размер прыжка.
7. Повторяйте шаги 3-6 до тех пор, пока текущий элемент не станет больше искомого значения или вы превысите границы списка.
8. Если текущий элемент больше искомого значения, выполните линейный поиск в предыдущем блоке с момента последнего прыжка.
9. Если элемент найден, верните его индекс (или значение, в зависимости от реализации).
10. Если элемент не найден, верните -1 (или другое значение, указывающее отсутствие элемента).
Прыжковый поиск имеет временную сложность O(√n), где "n" - количество элементов в списке. Он более эффективен, чем линейный поиск, но менее эффективен, чем бинарный поиск. Однако прыжковый поиск особенно полезен, когда список имеет равномерное распределение данных и доступ к элементам осуществляется за постоянное время.
Важно отметить, что прыжковый поиск также требует отсортированного списка для правильного функционирования.
В общем: да прибудет с вами сила.
Постепенно цикл буду дополнять.
Как яндекс доставляет товары
Или коротко об их "крутых алгоритмах".
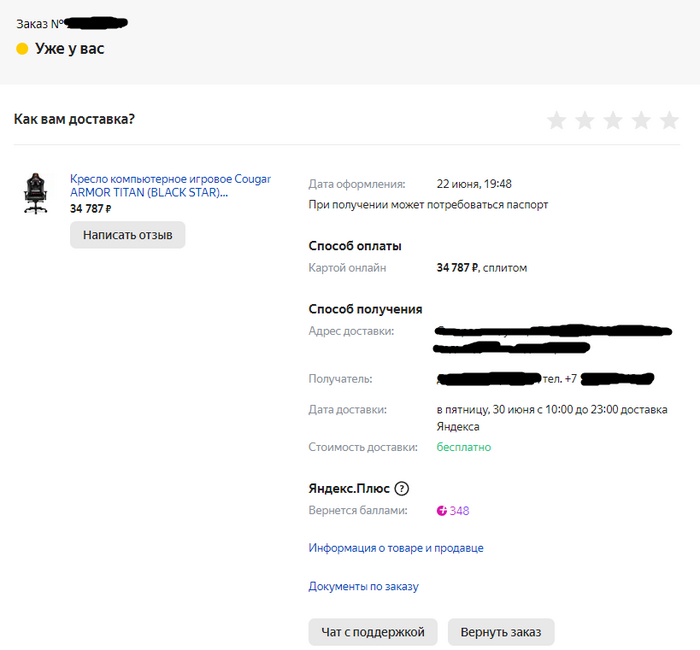
Уже в третий раз борюсь с доставкой яндекса. Три раза заказываю на дом, 3-и раза привозят не тот товар. Сегодня моя покупка обошлась в 34к, а привезли кондиционер в стоимостью 15к.
Весь день просидел на нервах с поддержкой.
1) Не прозрачная доставка курьера. Возит не по маршруту, проезжал мимо меня, в 200 метрах, после чего поехал в другой р-он нашего города.
2)Доставка предложила чисто вернуть деньги и товар, а искать мой - они просто отказались, при том, что покупка срочная, т.к. работаю из дома.
3)Больше никогда не буду ручаться за доставку яндекса, т.к. это самое худшее, что было в моей жизни.
Потратил кучу времени на доставку, привезли не тот товар, а теперь отказываются привозить мой. Говорят делать вовзрат, при том, что он уже подорожал))))
В ближайшее время пойду писать иск в суд, если мирным путём ничего не решится.
Алгоритмы и структуры в гошечке (golang) Pt1
Алгоритмы сортировки
Цимес: Тема крайне важна, в русскоязычном сегменте - мало представлена.
Таки будем исправлять.
Тема очень простая, важно начать, даже такой "укурок" как я осилил.
В общем - начнём мои чувачёчки...
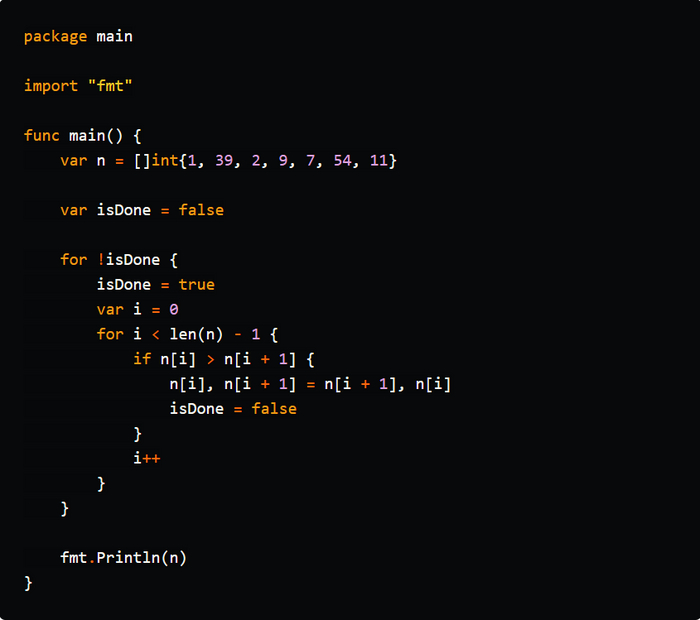
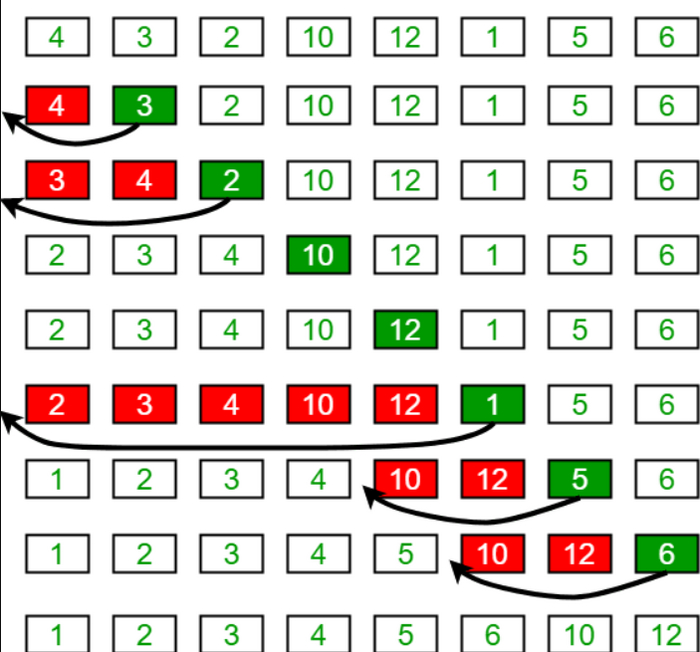
Сортировка "Пузырьком"
Сортировка "Пузырьком" - это очень простой алгоритм. Вам нужно сравнить каждый элемент массива со следующим элементом, чтобы увидеть, больше ли он, если да, то вам нужно поменять их местами. Вы должны продолжать выполнять эту задачу, пока больше нечего будет переставлять.
Халява, идём дальше.
Рекурсивная сортировка "пузырьком"
Рекурсивная сортировка пузырьком - это вариант обычной сортировки пузырьком (также известной как итеративная сортировка пузырьком). Она работает так же, как и итеративная сортировка пузырьком, без дополнительных преимуществ по времени или сложности. Однако это улучшит ваше понимание сортировки пузырьком и рекурсии.
Тоже простенько.
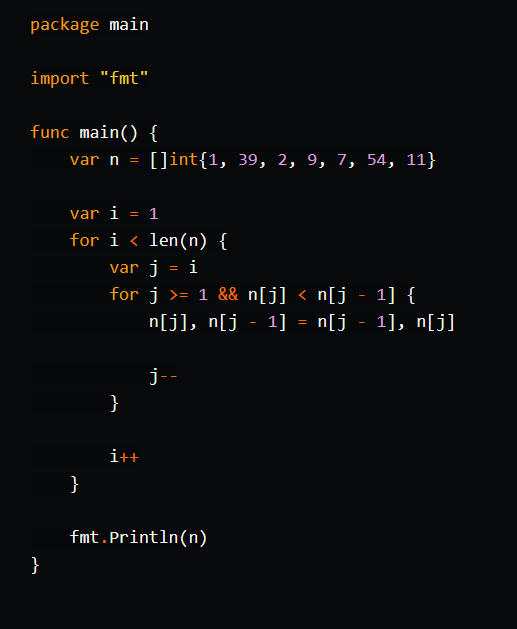
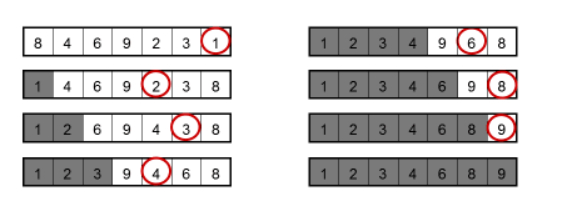
Сортировка вставками
Сортировка вставками (Insertion Sort) - это алгоритм сортировки, в котором элементы входного массива поочередно выбираются и вставляются в отсортированную последовательность элементов. Каждый новый элемент сравнивается с уже отсортированными элементами, и вставляется в нужное место в последовательности. Этот процесс продолжается до тех пор, пока все элементы не будут отсортированы.
По мне - так ещё проще, строк то меньше
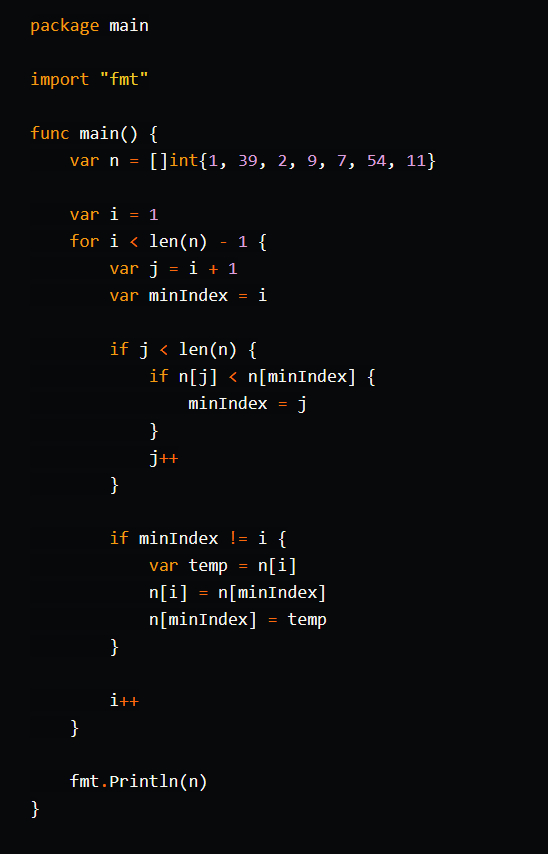
Сортировка выбором
Сортировка выбором (Selection Sort) - это алгоритм сортировки, который проходит по массиву и находит наименьший элемент, затем помещает его в начало массива. Затем алгоритм проходит по оставшейся части массива и находит следующий наименьший элемент, помещая его на следующую позицию в массиве. Этот процесс продолжается до тех пор, пока все элементы не будут отсортированы. Время выполнения сортировки выбором в худшем, среднем и лучшем случае составляет O(n^2), где n - количество элементов в массиве.
Чуточку сложнее... Продолжаем
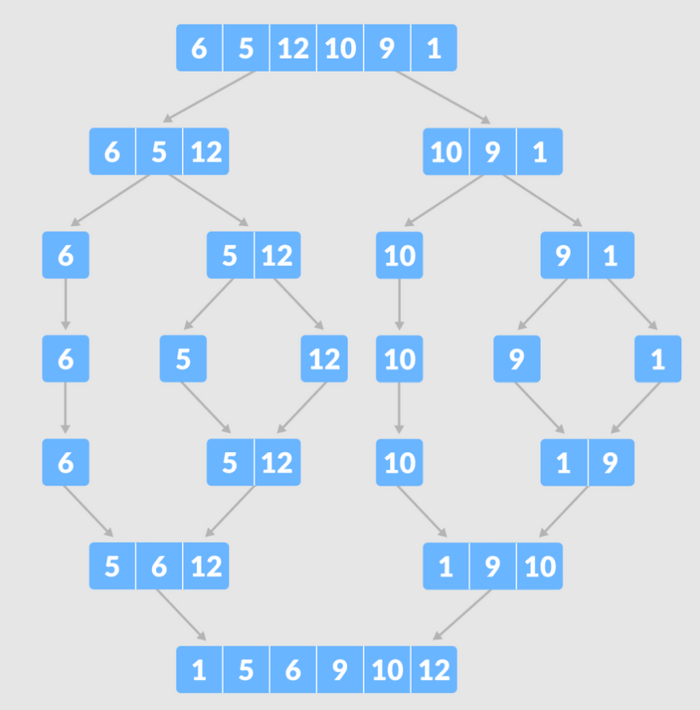
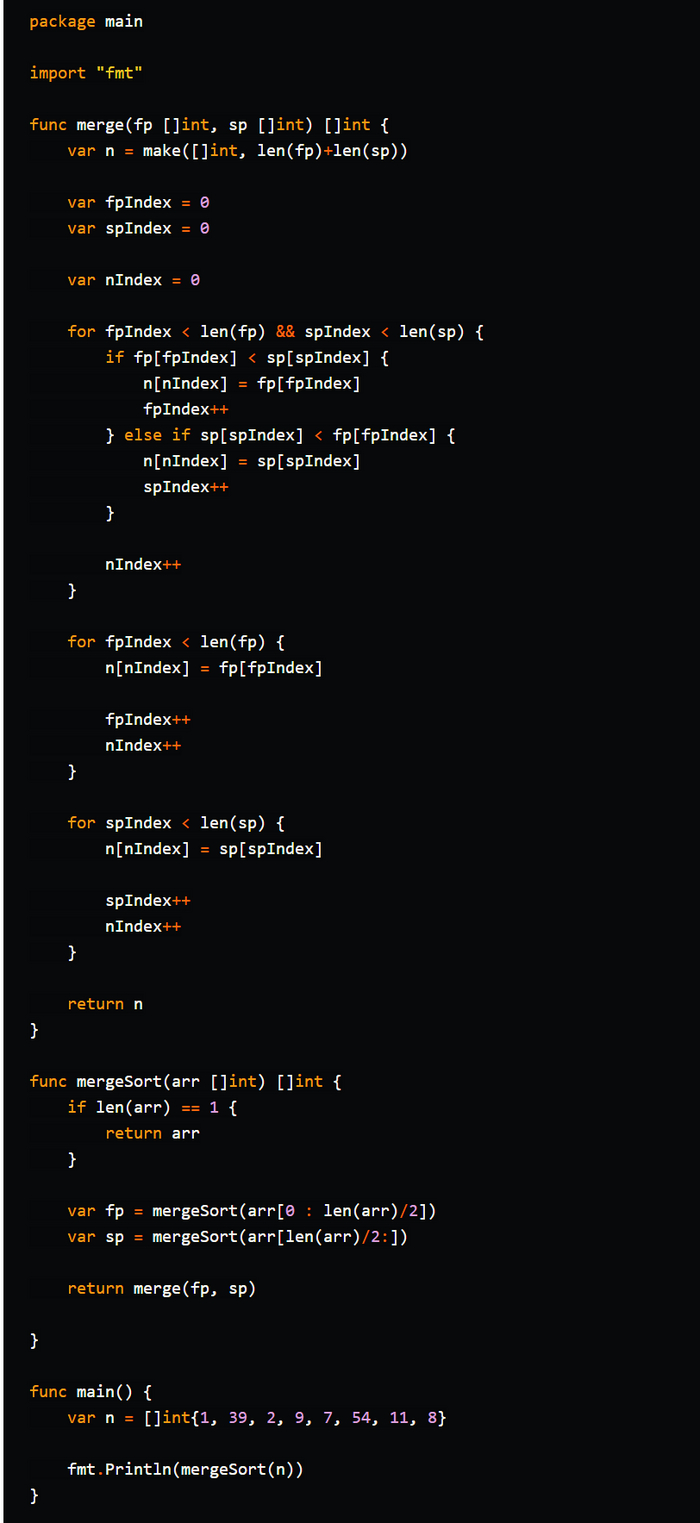
Сортировка слиянием
Сортировка слиянием (Merge Sort) - это алгоритм сортировки, который упорядочивает элементы массива путем разделения его на две половины, сортировки каждой половины отдельно, а затем слияния отсортированных половин в один отсортированный массив. Алгоритм сортировки слиянием является эффективным и обычно используется для сортировки больших массивов. Время выполнения сортировки слиянием в худшем, среднем и лучшем случае составляет O(n log n), где n - количество элементов в массиве.
Стало интереснее
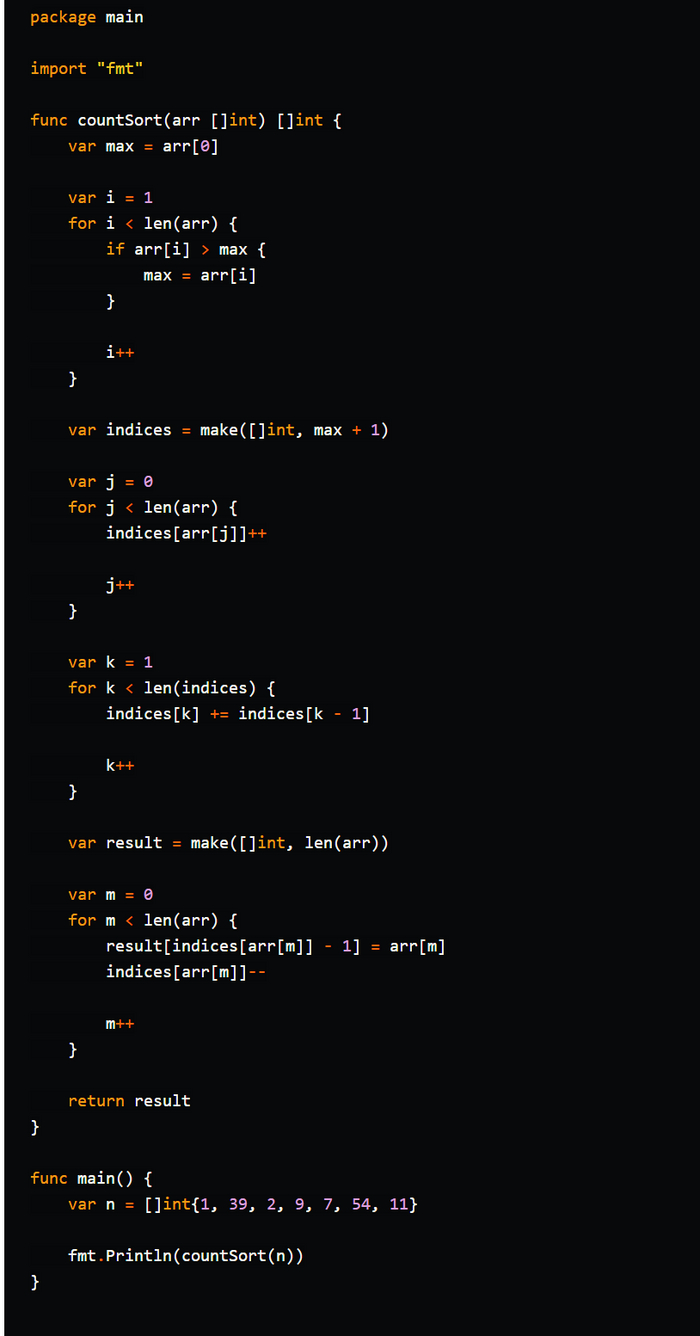
Сортировка подсчётом
Сортировка подсчётом (Counting Sort) - это алгоритм сортировки, который использует диапазон чисел в сортируемом массиве для подсчета количества совпадающих элементов. Затем элементы сортируются путем перебора диапазона и записи каждого элемента в выходной массив в соответствии с его количеством входных элементов. Алгоритм сортировки подсчетом является эффективным для сортировки массивов с небольшим диапазоном значений. Время выполнения сортировки подсчетом составляет O(n + k), где n - количество элементов в массиве, а k - размер диапазона значений.
В общем то на алгоритмах сортировки мы закончим, но это не всё!
Побольше кодим, поменьше задротим и всё у нас будет хорошо.
Вся эта умная выдача поиска примерно:
Перегорела лампочка в фаре. В ютубе нашел 2-минутный мануальчик как её поменять с минимальными усилиями. Поменял.
Ютуб следующие пол года: "Ты посмотри еще раз этот ролик! Тебе же понравилось! Продолжим с того места где ты закончил? Может хочешь еще лампочку в Ниве поменять? А в Шкоде? Во еще: автослесарь ремонитирует проводку в ЗИЛе! Ты же любишь всё такое! Топ 10 ошибок при замене лампочки не хочешь посмотреть? И для удобства, тот ролик, который ты уже посмотрел, я его теперь на главной закрепил, чтобы ты не потерял, ведь это для тебя так важно. Пожалуйста."
Минуса в горячем. Предположение откуда
Для л.л.: влупи этому посту минус. Плюс ни в коем случае!
Мне кажется, что алгоритмы настроены так, что рейтинг не учитывается в принципе, а учитывается количество реакций пользователей на пост в заданный промежуток времени. Давайте проверим это. Влупи этому посту минус. Плюс ни в коем случае!
Если я прав, этот пост вылетит в горячее. Иминус больше не минус - теперь минус это ничего не делать.
Такой подход может объясняться тем, что в горячее должны попадать посты вызывающие какие-то реакции, не важно положительные или отрицательные, тем самым будет развиваться срач дискуссия. На мой взгляд неправильный подход.
Тэг без рейтинга, чтобы не схватить пермобан, если я прав и сработает. Надеюсь я ничего не нарушил. Если что, пожалуйста не ругайте сильно)