Перемена мест слагаемых6
Я бы тоже так решил. Идиотизм.
Я очень надеюсь, что ваша знакомая из тех матерей, которые не будут говорить сыну, что он тупой, а забьют на оценки, если учителя идиоты.
Я подозреваю, что тут задание на закрепление правила о перемене мест слагаемых. А ребёнок сделал по своему, не использую это правило. А у учителя своя программа она должна объяснить, закрепить и проверить.
раскрыть ветку (2)
А еще задание 4 решено не полностью, но препод не заметил. Так что в итоге все равно оценка адекватная.
раскрыть ветку (1)
ещё комментарии
Это у взрослых для умножения действуют сочетательные свойства умножения (специально), а в начальной школе детей третируют, если они множители местами переставляют.... сказочный идиотизм. Цитируем Лаврова.
Чо сука самый умный? Сказано 2 на 5 а не наоборот. Какие законы? Да в рот я их ебала. Делай как говорят и не выделялся.
Ебучий совок в бошках.
Мне вот интересно, а родители в общем чате пишут об этом? Например «ИО классного руководителя, это что за хрень? (Скрин картинки) У вас там математичка математику сама-то знает?
а еще можно 5 первых шариков+ 5 вторых шариков= 10 шариков.
Или у вас так за сраную четверку во втором классе горит?
раскрыть ветку (9)
У нас учитель алгебры поменялся в 10 классе.
Я по привычке очевидные вычисления пропускаю и решаю задачку быстрее всех, за что учитель поставил мне тройку.
Пошел спрашивать что не так - говорит нужно каждый шаг записывать (грубо говоря 2*5+7*3 = 10 + 21 = 31, а я записал 2*5+7*3=31).
Я спросил "а зачем? и так же все понятно", на что получил "нужно".
Правда потом он привык что я пропускаю некоторые вычисления, которые в уме легко сделать, и не снижал за это оценки.
раскрыть ветку (4)
Вау! Ну прям один в один мой случай. Только у нас была учительница и поставила она четверку. И она тоже быстро привыкла к тому, что я действительно могу все это сокращать в уме. Правда для соседа иногда приходилось расписывать подробнее в его варианте решения задач - она точно не поверила бы, что это он сам так решал.
ну ты не путай десятый класс и второй.. мне моя математичка даже за неправильные вычисления не снижала например
раскрыть ветку (2)
Ну согласись в 10 классе расписывать как ты складывал два числа умноженных друг на друга это немного глупо.
Особенно когда речь идет уже о вычислениях интегралов и логарифмов.
раскрыть ветку (1)
ну в общем-то да, даже на егэ (в мой год, во всяком случае) подразумевается, что ученик в состоянии в уме решить АЖ КВАДРАТНОЕ УРАВНЕНИЕ
ещё комментарии
ещё комментарии
ваше решение или ребёнка?
детей учат понимать, что они считают, это начальные классы, вам это написали, чтобы он умножал правильно и понимал, что он считает шарики, а не ребят, дети не думают цифрами, их учат воспринимать их правильно
раскрыть ветку (1)
я специально написал тупорылое решение, что б было понятно, что ВО ВТОРОМ КЛАССЕ в этой задаче 2*5 более правильно, чем 5*2
ещё комментарии
ещё комментарии
Да, у меня 1 и 3 классы, порой так завернул задачу, что сам сижу и думаю что они хотят от детей.
Умножить число а на число б значит число а слагаемым б раз. Т.е. 3*4=3+3+3+3, а 4*3=4+4+4.
Все логично. Это математика. Тут нужно действовать по правилам. Потом уже узнают что 3+3+3+3=4+4+4=3*4=4*3=12
И назовут эту магию "переместительным законом умножения"
И на само деле это важно, иначе не будет понимания математики а будут механические манипуляции и заучивание.
раскрыть ветку (81)
раскрыть ветку (13)
раскрыть ветку (11)
откуда такое слово взяли-"множимое". Меня сразу учили что есть два множителя. И 3*4 это 3+3+3+3 или 4+4+4. Зачем давать лишную бесполезную информацию?
раскрыть ветку (10)
"два множителя" это упрощение, связанное с коммутативностью умножения в поле скалярных величин, которое приведет к ошибкам впоследствии. Когда два множителя перестанут быть равнозначными, будет тяжело в них не путаться.
Как правильно вычислить момент силы? Сила*плечо или плечо*сила?
раскрыть ветку (7)
Момент силы вычисляется из его определения. Это уже пошло словоблудие. А записать можно в любом порядке. Иногда даже удобней сгруппировать в неканонической записи, чтоб наглядней выглядело, для дальнейших выкладок.
ещё комментарии
В том-то и дело, что от порядка записи зависит знак выражения, и если изначально не научить человека тому, что этот порядок важен, у него будут возникать глупые ошибки
раскрыть ветку (5)
раскрыть ветку (4)
Дело в том, что при векторном произведении условно говоря минус на плюс будет минус, а плюс на минус будет плюс.
То есть [ab] = -[ba]
раскрыть ветку (3)
ещё комментарии
Так, для натуральных чисел умножение определяется как многократное сложение — чтобы умножить число a на число b надо сложить b чисел a
Ну и вы наверное не разгоняли процессоры в молодости :) Там уж множитель это одно, а множимое - другое.
раскрыть ветку (1)
Но мы сейчас говорим про начальную школу, где дети должны усвоить основные правила. А от избытка лишней информации у них будет одна каша в голове.
ещё комментарии
ещё комментарии
Мешает вот что. Если уж совсем упрощенно, то умножение выглядит так:
одинаковое слагаемое * сколько раз оно повторяется. При решении задач (при незнании переместит.закона умножения) это принципиально.
одинаковое слагаемое * сколько раз оно повторяется. При решении задач (при незнании переместит.закона умножения) это принципиально.
И на само деле это важно, иначе не будет понимания математики а будут механические манипуляции и заучивание.
А если ребенок уже знает про коммутативность умножения? Все равно неправильно?
раскрыть ветку (18)
У меня как-то в школе не засчитали задачу по геометрии, потому что я в ней применял правила, которые "мы еще не проходили". Ох у меня пригорало тогда.
раскрыть ветку (5)
У тебя проверяли знания текущих правил. Учителю важно понимать усвоен ли текущий материал. Нормальному учителю зачастую не важен ответ, ему важен ход решения.
раскрыть ветку (1)
Вот это тоже знакомая тема. Цель заданий в школе не получить результат, а просто вдолбить в голову ученика тему. Имхо это неправильно. Человека нужно учить оценивать любую задачу, искать оптимальное решение.
раскрыть ветку (2)
1. Способов решения задачи всегда несколько. Если в задаче не указано каким способом ее решать, то могу решать любым.
2. Был очень демотивирующий эффект на чтение учебника дальше положенного. Я понял, что если я учу что-то сам, то должен запоминать что мы проходили в школе, а что я читаю сам.
2. Был очень демотивирующий эффект на чтение учебника дальше положенного. Я понял, что если я учу что-то сам, то должен запоминать что мы проходили в школе, а что я читаю сам.
Самое интересное, что потом на контрольных, и гос экзаменах всем как раз уже было срать на ход решения и важен был правильный результат
Ну я думаю, что если во втором классе школьник найдет площадь прямоугольника интегрированием, то ему тоже не засчитают задание :)
раскрыть ветку (1)
Если он это повторил у доски самостоятельно, то я бы не просто засчитал, я бы его по имени-отчеству стал называть)))
Да. Ты должен показать, что понял учителя.
Умный - напиши рядом второй вариант или попробуй доказать учителю, что ты тоже прав, но вариант, которому тебя учили, ты должен привести тоже. Задача-то в школе не просто ответ получить, а показать, что ты понял процесс получения :)
раскрыть ветку (7)
Фигня какая-то, как по мне. Имхо, если проходите умножение, то сразу говорите, что оно коммутативно. А то пару лет вдалбливают, что порядок множителей имеет значение, потом резко говорят, что не имеет. А потом идешь на вышку и оказывается, что где-то имеет, а где-то нет. Доколе?!?!?!?! )))
раскрыть ветку (6)
Вы давно в последний раз вспоминали как вас учили буквы писать? Если давно - загуглите прописи. И ведь долго учили. Сравните со своим нынешним почерком. Правда дураки?
раскрыть ветку (5)
Я, видимо, еще до конца не проснулся, связи не вижу...
И кого я дураками назвал? Просто ребенок решил задачу? Решил. Ответ правильный? Правильный. Другим способом решил? Ну напиши просто рядом, что мы тут тему другую проходим, или спроси, с пониманием он это сделал или кто-то подсказал. А не черкай все нафиг, убивая в маленьком человеке немного иной взгляд на вещи. Вдалбливать делать все под копирку неправильно, нужно учить получать результат и критически мыслить.
раскрыть ветку (4)
И кого я дураками назвал?
По-моему, это я назвал :)
В школе главное не ответ, а решение. Умеешь решать другим способом? Молодец, но не забудь показать, что ты понял и то, что тебе рассказывали на уроке. Ответ без решения это очевидная двойка. Решение, в котором ошиблись с ответом может быть и четыре и пять с минусом, в зависимости от серьёзности ошибки.
В школе тебя учат думать и рассуждать, а "ответ" ты и на калькуляторе получишь :)
раскрыть ветку (3)
В школе тебя учат думать и рассуждать
Исходя из ваших слов в школе учат работать по алгоритму. Шаг влево, шаг вправо - расстрел.
Ладно, не буду спорить. Я не педагог и не психолог. Просто по своему опыту сужу. Когда пришел на мат. фак. учиться, то понял, что в школе что-то не то. М.б. меня только так учили, а другие школы клевые, хз. )
раскрыть ветку (2)
Можно подумать на матфаке "главное это ответ" прокатывало :) Вы мне сказки-то не рассказывайте, у меня за плечами матшкола и кафедра прикладной математики :)
раскрыть ветку (1)
Если в задаче вопрос "сколько", то главное ответ. Если "докажи", то нужно доказать. Если важен способ решения, то всегда писали каким методом решить. Если что-то свое придумаешь, так с преподавателем еще пообсуждаешь. Никогда никто не говорил "это неправильно, потому что не так, как я учил/учила".
тогда он не понимает какую задачу перед ним ставит учитель. от него требуют не число , его вообще можно не ставить , а правильно расставленные множители.
раскрыть ветку (1)
В задаче вопрос "Сколько". Ответ - число. Хотите правильный ответ - задайте правильный вопрос.
и да, у сына в классе учительница так и сказала, что в младших классах учат не просто перемножить, а понимать что и сколько раз взято и при проверке неправильная расстановка множителей считается грубой ошибкой, тогда как в средней и старшей школе, на это уже не обращают внимания, потому что дети уже понимают что к чему)
раскрыть ветку (2)
вот объясните пожалуйста, с какой целью в умножении нужно понимать "что и сколько раз взято"? для чего это понимание нужно? количество - величина безразмерная вообще-то.
раскрыть ветку (1)
при решении примеров, это не важно. При решении задач на 1е место ставится то, что нужно найти. Нужно найти кол-во ящиков- ставите ящики, если кг- значит кг. Для средних и старших классов это однофигственно, а в началке считают за ошибку.
Понимание математики приходит с понимаем того, что операции сложения и умножения имею свойство коммутативности (это как раз про а*в = в*а).
Но, как я вижу, тут и некоторые взрослые-то даже слова такого не знают. Придумывают какие-то "преместительные законы" и на серьезных щщах рассуждают про понимание математики.
раскрыть ветку (9)
UPD: Немного перегнул. Оказывается в учебниках действительно фигурирует термин "переместительный закон". Извините, если грубо выразился.
раскрыть ветку (6)
Ну только не говори что в школе тебе сразу во 2 классе про коммутативность и дистрибутивность рассказывали
раскрыть ветку (5)
Я как бы с садика подозревал об отрицательных числах. Я видел термометр, слышал о долгах и прочем. В школе мне упорно гоалрили "рано", а меня все мучал вопрос о отрицательных велечинах и я изучил их сам(в прямом смысле, сел и вывел, на умножение правда мозгов не хватило).
Тоже самое с умножением. Я еще таблицу изучая(правда нам уже преподавал список примеров) нашел закономерности и понял, что учить можно ровно половину.
В более старших классах я пытал преподов на предмет "а хули площадь круга именно такая", в ответ "рано". Ну еб вашу мать объясни ты про интеграл
раскрыть ветку (4)
Проблема сугубо в том, что программа общеобразовательная, и тут как раз надо учителю равняться на средний уровень, а вы как ученик с отрицательными числами вносили смуту.
раскрыть ветку (2)
По рассказам родителей я умел дикую штуку. Умножать на пальцах двузначные числа, причём быстро и точно. Учительницу это жутко бесило и она требовала отучить и родители отучили, о чем сильно жалеют. Сейчас ни они, ни я не помнят как я это делал и какой системой пользовался, но по историям я делал это осмыслено.
Вот так в нашей семье была утеряна технология пальцевого умножения.
P.S. к чести родителей они сперва говорили учителю "а вы сами можете как он? На бумажке в столбик и дурак сможет, а вы на пальцах устно"
раскрыть ветку (1)
Согласен, с вами, быть одаренным не всегда легко, учительницу бесило, что своими действиями вы подрывали ее авторитет.
Отрицательные числа интуитивно понятная вещь, я тоже с садика о них знал.
Но сомневаюсь что тебе именно слово "коммутативность" говорили
Первый адекватный комментарий по методике преподавания.
Сначала родители убеждают своих детей, что учителя - дебилы, а потом удивляются, что дети учителей ни во что не ставят и, соответственно, за всю школу ничему не научились.
раскрыть ветку (8)
раскрыть ветку (7)
Как раз тут учитель ничего не придумывал. Комментатор выше же ясно объяснил, что такое умножение: a * b = a + a + a + ... + a (b раз)
Свойство коммутативности умножения они ещё не прошли, не доказали, поэтому его применение неправильно в данном случае.
Я не раз сталкивалась со школьниками, которые не могут решить элементарные задачи просто потому, что не способны понять, что и в какой последовательности надо делать. У этого непонимания ноги растут как раз из вот таких "мелочей", как этот пример.
А родители (и другие взрослые), возмущающиеся тому, что учитель "всякий бред пишет" и "неправильно оценивает работы" способствуют тому, что школьники в дальнейшем не могут простроить себе нормально математическую систему.
ещё комментарии
"Я не раз сталкивалась со школьниками, которые не могут решить элементарные задачи просто потому, что не способны понять, что и в какой последовательности надо делать."
Потому что дебильные учителя учат по дебильным программам.
Которые "разрабатываются" каждый год ради написания очередных дебильных диссертаций.
И ради выпуска новых учебников, побольше и потяжелее. И, естественно, подороже.
Свойство коммутативности умножения они ещё не прошли, не доказали,
Коммутативность умножения — это аксиома. Она не доказывается.
раскрыть ветку (4)
Откуда у вас такие странные представления?
Доказывается коммутативность и сложения, и умножения
раскрыть ветку (2)
Вот, к примеру, из «Математического анализа» Зорича. В принципе, есть и другие способы построения множества действительных чисел, но я нигде не встречал, чтобы коммутативность была теоремой.
раскрыть ветку (1)
Тут другое определение умножения, видите же.
Если определять умножение через сложение, то нужно доказывать.
Тем, кто молча влепил мне 8 минусов: ну так приведите доказательство коммутативности. Или ставите минусы просто так, ничем не обосновывая?
ещё комментарии
люди не могут понять простого: взять 3 пенала 4 раза не то же самое.что взять 4 ручки по 3 раза
раскрыть ветку (1)
Проблема в том, что никто родителям не объясняет этот подход, а родители подсказвают и объясняют решение на основе своих знаний
раскрыть ветку (3)
Я думаю, что родители просто забывают со временем. Эта тема, как кто-то из учителей тут объяснял, не меняется давным давно, ещё с советских времён.
P.S. Я, к примеру, только глядя на пост вспомнил, что в школе писали знак умножения как току.
раскрыть ветку (2)
Не было такого в советские времена! Я в семидесятых начала учиться, никогда нам такое не исправляли. У меня старые тетради долгое время хранились, за перестановку чисел никаких санкций не было. Я отличница была до пятого класса, если бы за это снижали оценки, я бы не была отличницей, ибо про эти методы я узнаю только сейчас из таких вот постов.
раскрыть ветку (1)
Я не помню. Честно. Я в 78-м в первый класс пошёл - не помню. Но родители нынешних детей в большинстве своём учились позднее нас с вами.
Прошу прощения, прочитал про "переместительный закон умножения" и в выводе его написано: "От перестановки сомножителей произведение не меняется". И что в итоге то, какая разница ящики на апельсины умножать или апельсины на ящики? Это на столько смешно, что профессор по высшей математике от смеха падает.
раскрыть ветку (1)
Вобще-то от того, что на что умножать зависит количество битых апельсинов. Первое, с чем я столкнулся в высшей математике - это как раз отсутствие "переместительного закона умножения". Для каждого поля еще нужно доказать, работает этот закон или же нет (и в большинстве случаев он не работает, а работает только на скалярах)
Спасибо вам за этот комментарий! Всегда жопа горит от подобных публикаций! Сейчас только ленивый не пнет учителя.
Когда я объясняю ученикам деление в программировании целочисленное/вещественное, я провожу аналогии со школой, когда говорили что делить можно только нацело, потом оказалось что можно, а дальше начались извлечение корней из отрицательных чисел и деления на ноль. Тут так же, надо усвоить корректно материал, понять что и откуда, а потом двигаться дальше. А то в голове каша будет.
То есть надо взять 4 ручки три раза. Я правильно понимаю? А можно взять 3 раза 4 ручки. Не вижу разницы.
раскрыть ветку (4)
раскрыть ветку (3)
Закончил прикладную математику. И похоже не помогло. Подскажите. Господин ehanpalich написал правильный ответ?
раскрыть ветку (1)
Уважаемый hackoff подробно расписал в чем разница, я тоже как смог объяснил.
Не вижу смысла повторяться.
ещё комментарий
Это не заучивание, а критическое мышление. Благо моя учительница была не ебанутой и главной задачей у нее было научить детей решать, а не добываться по мелочам.
Спасибо, мил человек! Я сначала возмутился, мол какого хера!!! А про себя умножал 4х3 и не мог объяснить, что тут всё таки не так.
ещё комментарии
и переместительный закон становится понятен уже в графической форме когда видишь что это получаются столбцы и строчки. Все нормально. Думается это верная задача и скорей на следование правилам и логике чем вычислениям.
раскрыть ветку (1)
Он понятен уже на примере таблицы умножения, которая зеркальна относительно своей главной диоганали
раскрыть ветку (13)
О да, детям же не надо показывать, что иногда бывает недостаточно данных для решения задачи.
раскрыть ветку (2)
А что не так с 4, Дурман Гашишевич? Да и 3 просто сформулирована неявно, т.к. предполагает, что в мире всего 2 вида конфет - шоколадные и леденцы.
раскрыть ветку (8)
В 3м да сформировано неявно, но в 4м же дичь без возможного решения вообще, почитайте внимательнее
раскрыть ветку (1)
Очепятка. Если обратиться к учителю, она зачеркнет Свету и напишет Нину.
Хотя ни учитель, ни школьник 100% этого не заметят. Если, конечно, они на уроке перед этим не решали задачи из разряда "ответ = объяснение, чего не хватает для решения", тогда это просто повторение пройденного. Не всегда ответ может быть однозначным.
Я хотел конечно про ЛСД рассказать отпрыску, и пояснить за фарцующих марками на дискотеке девах (ну а куда им еще столько то), но пусть марки в его строящемся восприятии мира будут почтовыми пока.
раскрыть ветку (4)
На уроке. Учительница:
- Дети, у меня в руках кирпич. О чем вы думаете, когда смотрите на него?
Светочка:
- Я думаю о великом подвиге советских строителей!
Олечка:
- А я думаю о перспективах коммунистического строительства в нашей стране.
Вовочка:
- А я - о бабах.
Учительница:
- Вовочка, но почему?
Вовочка:
- А я всегда о них думаю.
Проще надо быть. А то марка - наркота, баян, трава, колесо, крокодил... Нормальным людям вообще слова остались?
раскрыть ветку (3)
Развиваться можно и нужно. Знание сленга определенных кругов сродни знанию еще одного языка. Другое дело если ты начинаешь его использовать не там, где следует. И вообще, не я это начал, так ведь, Баян Амфетаминович).
раскрыть ветку (2)
Ну, у Delwind'а претензия именно к маркам. Представляю, как он отреагирует на задания вроде написать рассказ "My trip" на английском, или "Закрасить небо на рисунке ГОЛУБЫМ цветом" по ИЗО.
раскрыть ветку (1)
Есть такая тема в первом классе "Определить что является задачей и ее можно решить, а какие задания не являются задачей"
Значит так учатся, раз вызывает отвращение учеба. Или учителя не заинтересовывают предметом. У меня во втором классе большинство обожают кто математику, кто русский и прекрасно понимают разницу в записях к задаче 3*4 или 4*3.
Нужно не решение, а алгоритм действий, поэтому, 5+6 это не одиннадцать, а один десяток и одна единица. Если они проходят сложение, то нужно решить именно сложением. То же и с чтением, когда ребенок читает, на Ваш взгляд правильно, но не может читать по слогам, за чтение он будет получать 2.
Я у племянника как-то в учебнике нашла ошибку в примере, который печатается в объяснении темы
Просто тему проходят сложение, а не умножение. То есть нужно было написать 4+4+4=12. Понимаю что девочка знает больше, чем прошли в классе.
Греф же сказал, что население должно быть тупым скотом и ничего не понимать ни в экономике, ни в государственной жизни. Только жвачка от Киселёва
Народной смешной. Здесь ответ и решения неправильные. Учат с начальной школы чтобы потом путаницы не было с размерностью. Как бы считали если бы здесь не цело число было?
Отдельной похвалы заслуживают учителя в комментариях и те кто обсирают систему образования.
раскрыть ветку (60)
Какой размерностью?
У нас есть количество ручек на пенал(р/п) и пеналов(п).
Тепрь умножим
3п×4р/п и 4р/п×3п = 4р
И так и сяк пеналы сократятся и будут ручки.
раскрыть ветку (2)
ещё комментарии
ещё комментарии
Здесь ответ и решения неправильные.То есть по 4 ручки в трёх пеналах - это не 12 ручек?
Озвучь же правильный ответ.
ещё комментарии
Ответ верен, но метод который использовался нет. Надо ручки умножать на кол-во пеналов, так как именно за этим действием стоит 4 ручки + 4 ручки + 4 ручки.
раскрыть ветку (18)
Всё нормально размерностями:
4 ручки/пенал * 3 пенала = 12 ручек
3 пенала * 4 ручки/пенал = 12 ручек
От перемены местами множителей размерность не меняется.
Хоть вы метры в секунду умножать на секунду будете, хоть секунды на метр в секунду, всё равно получите метры.
ещё комментарии
Какие размерности? "Физический" смысл умножения ручек на пеналы состоит в том, что вы берете ручки из разных пеналов и складываете в одну кучу. Здесь еще у детей нет абстракции в мышлении, а вы уже привыкли оперировать в голове абстрактными множителями с определенным свойствами. Детям надо еще только перейти от объекта к абстрактной сущности, которой оперирует математика.
раскрыть ветку (3)
Знаете как бесит школьный подход, а давайте вы забудете, что было раньше? Сначала учат одно, а потом тоже самое, но по другому. Конечно в начальной школе высшую математику не надо давать, но и подобной тупости нужно как можно меньше. Понять коммутативность произведения и сложения дети способны.
раскрыть ветку (2)
Проще по моему сперва учить коммутативности, а в институте уже сказать о том, что правило работает не всегда
ещё комментарий
смотри у тебя есть 12 ручек, ты их раскладываешь в пеналы (делишь ручки на пеналы). Смекаешь? Вот потому и умножаешь количество ручек на количество пеналов, между которыми ты можешь поделить эти ручки.
ещё комментарии
Для минусующих поясняю: 3 пенала умножить на 4 = 12 пеналов. 4 ручки умножить 3 = 12 ручек
раскрыть ветку (5)
Под пеналом подразумевается множество из 4 ручек => в ответе получаются ручки, а не пеналы
Ещё раз вам повторю: 3 пенала умножить на 4 ручки в пенале = 12 ручек.
А то по вашей логике, если машина 3 часа ехала со скоростью 60 км/ч.
То она проехала или расстояние:
60км/ч*3=180км/ч
или
3ч*60=180ч
а километры мы вообще никак не получим.
ещё комментарии
Ты рили ебну%$#?
Почему ты в 60км/ч размерность учел, а в 3ч нет и наоборот? Тип кручу верчу наебать хочу?
раскрыть ветку (2)
Всё верно. Я просто привёл пример как человек неправильно обращается с размерностями.
А у многих тут в комментариях если по одному перемножать, то получаются ручки, а по другому пеналы.
Хотя там точно так же как в моём примере «километры в час» и «часы» в этой задаче «ручки в пенале» и «пеналы» и в каком порядке их не перемножай выйдут «ручки».
ещё комментарии
ещё комментарии
ещё комментарии
Да какая разница? И так понятно что на что умножается. Это безосновательный повод доебаться, а не логика.
ещё комментарии
Это вы говорите только потому, что считаете результат умножения независящим от перестановки множителей. Для натуральных чисел это справедливо, но в общем случае нет.
раскрыть ветку (4)
раскрыть ветку (2)
Матрицы и другие множества, это первое что приходит на ум. Наверняка еще куча каких вариантов. Обычно чем больше погружаешься в математику тем больше понимаешь: то, что раньше было обычным, стало исключением из правил.
раскрыть ветку (1)
Это справедливо для любых чисел и размерностей. Просто размерности надо правильно записывать.
ещё комментарии
ещё комментарии
где проблема с размерностью?
В трех пеналах по 4 ручки - берём три раза по 4 ручки - где проблема с размерностью?
ещё комментарии
есть три шлюхи, каждой ты кинул по палке, при смене множителя и множимого, каждая шлюха кинула палку тебе. Общее количество палок не меняется, но в первом варианте ты довольно улыбаешься, а во втором твоя жопа похожа на скворечник
раскрыть ветку (8)
есть три шлюхи, каждой ты кинул по палке, при смене множителя и множимого
получится что по палке получит каждая шлюха.
...А вам к сексопатологу надо! (С) Старый анекдот
ещё комментарии
и этой палкой оприходует тебя.
Школу прогуливали, теперь выёбываются знаниями, где только результат важен
раскрыть ветку (3)
ещё комментарии
ещё комментарии
ещё комментарий
Так как операция "кидания палок" не обладает коммутативностью для гетеросексуалов, ваш пример вызывает сомнения как минимум в вашей компетенции в области арифметики.
ещё комментарии
Ну давай, умный ты наш.
1) какой ответ правильный
2) найди ошибку в решении
3)с какой, нахуй, размерностью?
3.1 ты считаешь, что 3 Ньютона * на 10 метров ≠ 10м * 3Н?
3.2 ты считаешь, что 1.35*π≠π*1.35?
1) какой ответ правильный
2) найди ошибку в решении
3)с какой, нахуй, размерностью?
3.1 ты считаешь, что 3 Ньютона * на 10 метров ≠ 10м * 3Н?
3.2 ты считаешь, что 1.35*π≠π*1.35?
ещё комментарии
С числом тупанул. Ок.
Решение 4х3=12
правило порядока необходимо для понимания что на что надо умножать и что получишь.
Если бы это был абстрактный пример, то никаких вопросов.
раскрыть ветку (9)
раскрыть ветку (8)
Наряду с Правилом синей ручки, одно из важнейших. Всем же известно, что писать в тетради можно только Синей ручкой. Иначе двойку тебе, двойку!
ещё комментарии
Кстати на счёт таких правил. Если есть абсурдно правило, значит кто то так исхитрился, что пришлось его ввести.
раскрыть ветку (4)
Элементарно, это блядская политика "все у всех должно быть одинаково" одинаковая одежда/ручки/ карандаши. Все все все. У меня во втором классе доходило до обсурда что даже тетрати в 12 листов должны заканчиваться у всех одинаково (конкетрная учительница требовала) если у тебя подчерк широкий, твои проблемы, добавляй листики и ебить с ними
раскрыть ветку (3)
Не, ну синяя ручка действительно нормально читается на белой бумаге. Думается мне что использование синих чернил, а не черных, обусловлено тем что синие дешевле в производстве. Да и когда все одним цветом пишут мозг не взрывается от множества красок.
Как пример ублюдки пишущие тут в комментах с кучей смайлов. Просто мозг вылетает, когда подобное видишь.
Согласись что здесь уже просто учитель не адекватный.
Но здесь речь про одно правило, которое применяется только к таким задачам.
ещё комментарий
ещё комментарии
Там все задачи в начальной школе с "яблоками" и им объясняют что на что надо умножать или делить чтобы получились "яблоки".
Куча постов с умножение, но никогда нет проблем похожих с делением. Потому что деление лучше попадает под логику таких задач.
И те кто говорят мыслит по шаблону и прочее. Может их просто учат там логической цепочки, потому что она там есть. Ничего сложного в этом не вижу.
раскрыть ветку (1)
Казалось бы, при чем тут деление... В делении как раз важно, что на что делить. В умножении похуй, что на что умножать.
ещё комментарии
Предположим, что у 5,5 ребят по 2,5 шариков... И? Как перемена мест слагаемых повлияет на конечный ответ?
Учат быть баранами! Делай так как сказано, а не так считаешь нужным.
Мой младший брат тоже, классе в восьмом, решил уравнение не тем способом который описан в учебнике, но ответ был верный. Ему поставили 2. Сказали, что решил неправильно. Он при училке решил то же уравнение, показывая, что его способ тоже правильный. В итоге пошли к директору. Тот сказал, что - да, так тоже можно. И брату исправили оценку.
Вот только после этого случая, любовь к математике у него, поутихла. Потому, что нахер надо из себя, что-то строить, если это не оценят.
раскрыть ветку (5)
нахер надо из себя, что-то строить, если это не оценят.
так ведь люди учатся не для того, чтобы кто-то оценил!
раскрыть ветку (3)
Вы знаете, что такое мотивация?
Люди учатся не для того, чтобы кто-то оценил? Парадокс, но ведь в школе именно оценками измеряются знания. А если тебе, за правильный, но нестандартный ответ, ставят отрицательную оценку, то мотивация к обучению падает. Ребенок будет просто стараться получить хорошую оценку. И хорошо если, родители занимаются ребенком. А если всё обучение сводится к школьной программе, то в скором времени пропадает и гибкость ума и способность мыслить нестандартно. И по окончании одиннадцатого класса, выходит из школы чудо с хлебушком в голове (таким же как у его учителя).
раскрыть ветку (2)
мотивация? получить образование, чтобы потом не дворы мести, а в офисе сидеть! Чтобы в универ поступить и от армии бронь получить. Как тебе такая мотивация?
раскрыть ветку (1)
Ну, да. Образование ради образования, а не ради знаний. Я же не говорю, что плохо учатся. Получаешь, хорошие оценки и идёшь с ними в универ. В универе учишься по той же схеме - получить хорошую оценку, а не знания. И вот уже готов "офигенный специалист" который идёт работать или не по специальности или сидит в гос конторе за копейки, потому, что нихренища не знает. Потому, что его всю жизнь учили мыслить по шаблону. А всё вне шаблона - порицалось.
а не так считаешь нужным
Та зачем вообще в эту школу ходить? Пусть дитачка просто всё делает, как считает нужным.
В школьной программе размерность? По этой логике нужно детей сразу учить, что на 0 делить можно)
ещё комментарии
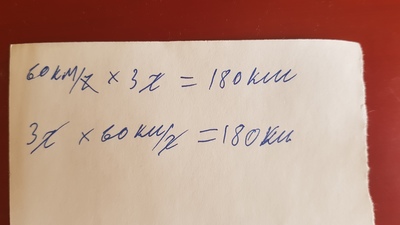
Школьный уголок
1.8K постов3.8K подписчика
Правила сообщества
Можно:
Писать всё, что можно отнести к школе.
...
Нельзя:
Нарушать правила Пикабу.