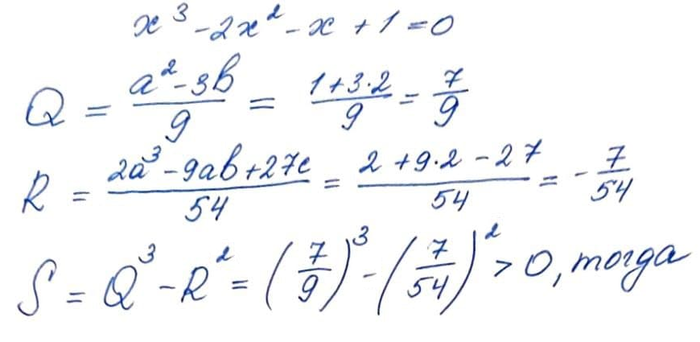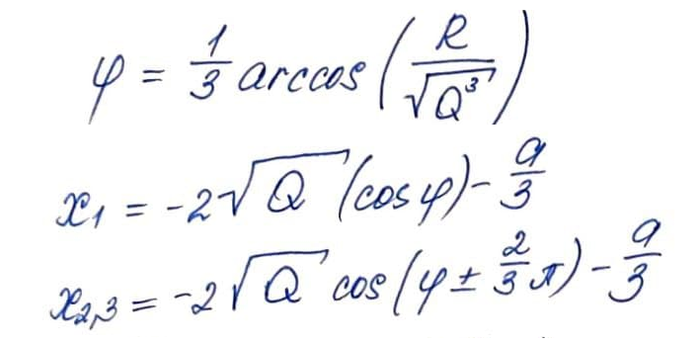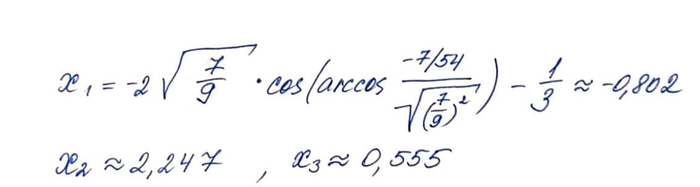Гениальная формула Виета, которую не проходили в школе
Приветствую Вас, уважаемые Читатели! Решение кубических уравнений со школы вызывало определенные сложности. Мало того, что среди корней таких уравнений часто встречаются числа с мнимой частью, так и формула Кардано для решения таких уравнений достаточно сложная и мудрёная.
Остается еще вариант разложить кубический многочлен на множители, использовать теорему Безу для подбора целых корней, но и это не всегда получается. Сегодня я хочу рассказать о тригонометрическом способе решения кубических уравнений, который разработал наш старый знакомый Франсуа Виет.
Добрый, усатый, твой - Франсуа Виет
Тригонометрическая формула Виета хоть и выводится достаточно просто, однако всё так же содержит громоздкие итоговые формулы. Чаще всего таким методом решения пользуются, чтобы получить приближенное значение корней уравнения, что достаточно для практических расчетов, итак:
В первую очередь вычисляются величины Q, R и S, от которых зависит, сколько и каких корней будет иметь уравнение (в нём а=1, b=-2, c=-1) . В нашем случае S>0, а значит шайтан-уравнение имеет три вещественных корня:
Вот такие формулы для корней этого уравнения. Если Вы думаете, что они сложные, то глубоко ошибаетесь. При других S в формулах появляются даже гиперболические арк-функции!
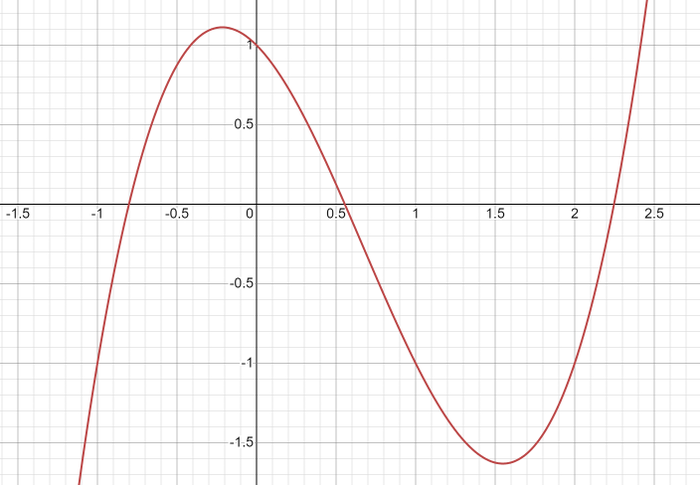
Получить здесь красивые числа для вычислений - большая удача, но с помощью калькулятора найти решение просто. Проверим на графике
А вот и график нашей функции. Нули совпадают с найденными нами по тригонометрической формуле Виета
Самое большое достоинство метода - это возможность запрограммировать алгоритм решения любого кубического уравнения со сколь угодно нужной степенью точности. Недаром, многие из представленных в интернете онлайн-калькуляторов решают кубические уравнения именно с помощью тригонометрической формулы Виета.
Больше интересной математики в телеграмм - "Математика не для всех"