1. Стремится к единице сумма первых N членов ряда при N стремящемся к бесконечности.
2. Сумма всего ряда целиком никуда не стремится, она в точности равна пределу, полученному на предыдущем шаге (т.е. единице).
Как мне нравится вот это:
"сумма первых N членов ряда при N стремящемся к бесконечности".
Важно, что сумма не всех до бесконечности, а именно первых до бесконечности. :)
Как можно сказать, что сумма ряда равна единице, если она бесконечна и всегда будет на бесконечно малую величину меньше одного?
Потому что "сумма ряда равна единице" и "она всегда будет меньше одного" - это две разные суммы. Частичная сумма ряда всегда будет меньше единицы, но стремится к ней при увеличении числа суммируемых членов. Полная сумма ряда (она же просто сумма ряда) равна пределу, к которому стремится частичная сумма. Она не стремится к пределу, потому что она и есть этот предел.
полная сумма ряда бесконечна
Нет. Полная сумма ряда - это предел. Предел - это конечное число, в данном случае равное единице. Ровно единице и ничуть меньше. Потому что сколь малую величину вы бы не отняли от единицы, будет существовать частичная сумма, превышающая ваш результат. Поэтому предел меньше единицы быть не может ни на сколь малую величину.
не достижима
Достижимость - это из теории графов. Если есть дорога из Москвы до Мухосранска, а из Мухосранска есть дорога до Хуежопинска, то Хуежопинск достижим из Москвы. К суммам рядов это никакого отношения не имеет, там понятия достижимости нет.
У рядов есть понятие сходимости. Если у частичных сумм ряда есть предел, то ряд называется сходящимся, а этот предел называется его суммой. Если такого предела нет, то ряд называется расходящимся. У ряда из поста такой предел есть, он равен единице. Сумма бесконечного ряда - это предел частичных сумм. Значит, эта сумма - единица. А единица - конечное число.
Да, вы не можете сложить бесконечное количество членов. Но вы можете поступить умнее и найти предел, к которому стремятся частные суммы, и его-то и назвать суммой бесконечного ряда. Математики так и сделали. И раз продолжают так делать, значит это работает.
Вы можете сказать, что это не имеет какого-то реального смысла. Но тогда можно дойти до того, что вы не можете иметь минус три яблока (вы можете только быть должны плюс три яблока) и более того не можете иметь ноль яблок (вы можете только не иметь яблок вообще). Можно сказать, что я довожу до абсурда, но ведь именно по этим причинам долгое время в математике не было ни отрицательных чисел, ни даже нуля. Но когда за ними всё-таки признали право на существование, то сразу жить стало легче и веселее.
Предел - это конечное число, в данном случае равное единице.
А есть такое официальное определение понятия "предел"? Интернет как-то не горит желанием им делиться.
Это типо первый месяц первого курса любого около математического направления в ВУЗе по предмету математический анализ. Но объяснять на словах максимально долго, особенно не используя кванторы. Где-то тут было определение предела в каноническом виде, но думаю, что вам от этого понятнее не стало =)
А что смущает? Предел последовательности в статье по ссылке определён вполне классически (см. рис.), а больше в данном случае ничего и не надо.
Пределом последовательности называют объект, к которому члены последовательности в некотором смысле стремятся или приближаются с ростом порядкового номера.
Смущает отсутствие знака равенства.
Не скажу, потому что вы всё правильно расписали, просто я не очень силён в длинных математических описаниях.
А так да, многие математические вещи, при попытке их применения к реальным объектам вполне себе абсурдны.
Потому, что математик не наука, а инструмент.
у нас уже есть целое, равное условной единице. От этого целого мы отрезаем определенную долю, а от того что отрезали снова отрезаем долю, и так до бесконечности. Если сложить все наши обрезки то получим исходную единицу
ээээ но мы же никогда не сможем физически отрезать бесконечность? Сколько ни считай, как ни тужься, но мы никогда не просчитаем бесконечность, у нас всегда от единички будет что-то оставаться.
По его мнению, само существование математики со всеми её логичными теоремами и доказательствами является доказательством существования бога. Иначе в математике всё так не укладывалось бы по полочкам. Nuff said.
Это нам она кажется простой и логичной. Просто потому, что вся математика является следствием строения нашего мира.
Не мир такой, каким мы его видим, потому что есть математика и она вот такая. Но математика такая, какая есть, потому что мир такой, какой он есть.
А простым и логичным нам кажется то, что хорошо ложится в наш разум, сформированный в процессе естественного отбора в условиях этого конкретного мира.
Нет. Математика как и формальная логика лежат над миром и являются общими для любого из миров (если они существуют). Это фундаментальные закономерности в самом фундаментном смысле слова. Если бы наш мир не существовал, закономерности математики оставались бы такими, какие они есть.
Имхо, связь математики с окружающим миром заканчивается на натуральных числах. Ну дроби с нулем еще куда ни шло, а отрицательные числа - уже все. Синусы, косинусы, пределы. Вот, скажите, где в нашем мире мы пользуемся квадратными уравнениями? А комплексные числа?
А теперь прочитайте определение естественных наук. Может до вас дойдет, что математика к ним не относится.
Все просто, так как вероятность перепихона со Скарлетт Йоханссон хоть и стремится, но не равна нулю, то получается, что таки да, я с ней потрахаюсь.
дроби мне нечего не доказали) у компьютера есть лимит операции он бесконечно умножать не может он в какой-то момент округлит) да если на калькуляторе делать что они говорят то будет 1 . ну допустим я вечно буду перемножать 0,(3) на 3 в какой момент я получу 10?
Если будете считать вручную, то вы никогда не получите какой-либо конечный результат. Будете считать бесконечно. Тут работает только аналитический подход.
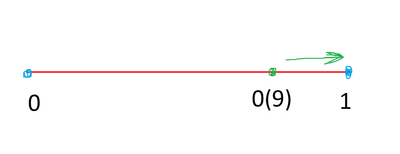
0,(9) бесконечно близко к 1
Нет такого понятия как "число бесконечно близко к числу". Никакая "бесконечно малая величина" не существует сама по себе. Для того, чтобы можно было сказать, что величина куда-то стремится (например разница между 1 и 0.(9) стремится к нулю, т.е. бесконечно мала) - необходимо, чтобы какой-то аргумент этой величины куда-то стремился - например "1/х стремится к нулю, если х стремится к бесконечности".
Единственная "бесконечно малая величина", существующая отдельно от аргумента - это чистый ноль и есть. Ноль разницы, тождественно равно.
Ну и если взглянуть с другой стороны - 0.(9) это уже и есть предел последовательностей 0.9, 0.99, 0.999, ... 0.999999999, ...
Вот разница между каждым элементом и единицей - она действительно "пока ещё стремится" к 0. А на бесконечности цифр после запятой - строго равна, как и любой другой предел.
так окей последний тупой вопрос что я получу если сделаю так 0.(9) + 0.(1) = ? :)) так любопытно )
Видел я это доказательство от Саватеева. Вопросы остались почему такую же логику нельзя применить к сопоставлению рациональных чисел с иррациональными. Он ответил что там очень сложная аксиоматика.
Мы утверждаем, что 0,(9)=1. Прибавим столбиком к обеим частям равенства 0,(1)
0,9999...
+
0,1111...
------------
1,1111...
В правой части, очевидно, получается 1,1111...
Вот и выходит, 1,(1)=1,(1)
Поскольку к обеим частям выражения прибавляли одно и то же число, тогда получается, что равенство 0,(9)=1 верно.
С пределом ряда похожая ситуация. В математике ничего не утверждается безосновательно. Хотите разобраться - вперёд, матанализ вам в помощь. И удачи...
Где то когда то в бесконечности она её достигает.
Тот факт, что ряд бесконечен, означает, что достигает в конце бесконечности (а бесконечность бесконечна).
Это как корень из -1. Это ФИЗИЧЕСКИ не возможно и абсурдно, но математически используемо.
Не путайте с асимптотой, которая стремится аки юный мальчик в женское лоно, но достигнуть не может.
Корень из -1 использует комплексные числа, которые также используются для решения уравнения волновой функции в квантовой физике. То есть физически это возможно )
Используется, но ты можешь физически представить корень из -1?
Ну то есть, сможешь описать такое число, которое при умножении давало бы -1?
И да, КОРЕНЬ из -1 не использует комплексные числа, он их порождает.
Само определение комплексного числа строится на корне из -1.
Физически чисел не существует, вообще никаких, а не только корня из -1. Числа это чистая абстракция.
И определение комплексного числа не строится на корне из -1. В определении мнимой единицы нет никакого корня.
Мни́мая едини́ца — комплексное число, квадрат которого равен -1
Ну то есть, сможешь описать такое число, которое при умножении давало бы -1?
Разумеется, оно равно i. Твоя проблема в том, что ты пытаешься доказать, что "i не является числом", обосновываясь на том, что "i это не число". Чистые сепульки.
А если обратиться к базовым определениям чисел в математике, то обнаружится, что алфавит цифр может быть примерно любой, а правила математических операций на ним - тем более.
Да, алфавит цифр может быть любым, но только вот i не цифра даже. i это неизвестная. Фактически, мы не знаем, чему равен корень из -1, но мы считаем, что он существует.
ты можешь физически представить корень из -1?Проще простого: https://youtu.be/kicp_odjsRs?t=92
К слову, квантовые взаимодействия судя по всем происходят в большем числе измерений пространства-времени чем 4.
Два числа различны, если между ними можно вставить ещё одно число.
Если ещё одно число вставить нельзя, то два числа равны.
Так: 0,(9)=1, например
Вставить всегда можно,если только речь не идёт о целом. Все эти расплывчатые формулировки из ВМ.
А сумма всех натуральных чисел равна вовсе не бесконечности и даже не стремится к нему, а равна -1/12. Прикинь)))
Можно офтопом воспользоваться вашими экспертными знаниями и спросить чему равна сумма квадратов бесконечного числа слагаемых, каждое из которых стремится к нулю, а их сумма равна единице? Т.е.
a+b+c+...=1
a²+b²+c²+...=?
каждое из которых стремится к нулю
А точно именно "каждое слагаемое стремится к нулю", а не "последовательность слагаемых стремится к нулю" ?)
Большая разница
Ну и осмелюсь предположить, что в общем виде ответа не будет, все зависит от конкретного вида последовательности a,b,c...
По условию слагаемые - доли целого. Задача найти (минимальное теоретически возможное) значение функции, равной сумме квадратов долей целого, если долей бесконечно много. Соответственно, сумма долей равна 1, число этих долей - бесконечно большое, а значение каждой из них - бесконечно малое.
Тогда звучит очень сложно
Я бы попробовал представить это в виде функции f(n, k), такой, что
- для любого k1 предел суммы f(n, k1) по всем n равен 1 (сумма в любой строке сходится к 1)
а предел f(n1, k) для любого n1 при k->inf равен 0 (вертикальный ряд сходится к 0)
а найти соответственно надо минимум от "сумм (f(n,k))^2 по всем n", среди всех k (т.е., считай, другая бесконечная "таблица")
тогда ряд наподобие того что в посте может оказаться одной из строк
и на его примере можно попробовать обобщить до f(n,k) = (k-1)/(k^n)
но кстати это не поможет доказать минимальность ответа, если он не окажется нулём
и это я только математическое представление задачи десять минут сочинял)
а как начать решать лично я ваще хз)
Как обычно, нужно что-то креативное, начинающееся со слов "заметим, что"
Если взять равные доли, то первое выражение можно будет представить как n*1/n = 1
А второе превратится n*1/n^2 => 1/n
При n стремящимся к бесконечности выражение будет стремиться к нулю
Ну и, насколько я помню, при сумме первого бесконечно малых второго порядка получится бесконечно малое первого порядка (но доказывать или искать доказательство мне лень)
А если убрать условие на то, что каждая часть бесконечно малая, то можно получить любое наперёд заданное число в интервале (0;1]
... А ещё у вас неотрицательность не упоминается, так там вообще можно любое наперёд заданное число получить :)
Ишто. Мы его сами введём для обозначения номера каждого слагаемого (а также их количества в отдельно взятой частичной сумме)
Многоточие включает в себя всё бесконечное множество последующих слагаемых. И на бесконечности сумма уже никуда не стремится, она строго равна 1, потому что уже "достремилась".
Именно. Вселенная крута тем, что несмотря на свою значительную математичность, она умеет больше, в том числе делать и не математические штуки, например позволяет ахиллесу догнать наконец черепаху
Нет, равно. Ведь выражение слева это уже предел. Многоточие намекает, что слева уже результат записан.