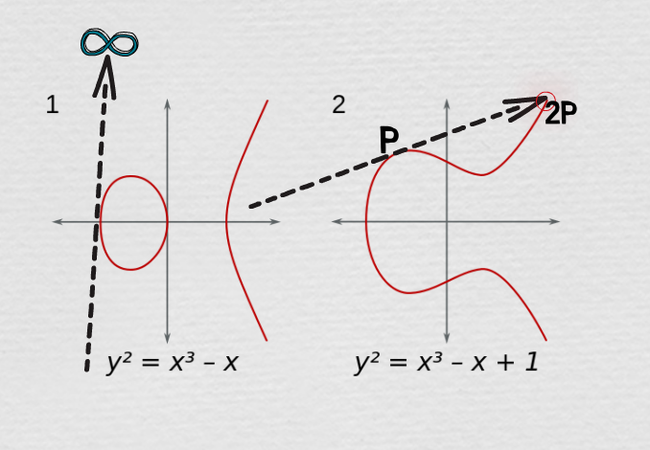Всем привет.

Если ты до сих пор гадаешь почему ты такой умный, но такой бедный, то этот пост для тебя. Ведь можно заработать 6 000 000 долларов, всего то за 6 задачек. Спеши, а то решит кто-то другой, одну уже решили. Но задачи эти не из цикла «только 2% людей могут решить их». Эти задачи вообще пока не могут решить. Сегодня мы попробуем понять о чём вообще эти задачи, и кто такой щедрый раздаёт за них по миллиону. Ну и как всегда пост имеет два формата, для тех кто любит читать, и для тех кто любит смотреть есть видео. Его я и рекомендовал бы в первую очередь.

Сперва немного истории для ввода в курс дела.

Некоторые люди, действительно парятся о том чтобы наука двигалась, и не потому что лично им с этого что то будет, просто они видят что от этого будет польза всему человечеству. И вот два таких Энтузиаста, а именно Лэндон Клэй и Артур Джеффи создали независимую организацию - математический институт Клэя. Ещё в 98-м году. Выдавали разные гранты многообещающим студентам, а в 2000-м и вообще, утвердили 7 задач и теорем, решение/доказательство или опровержение которых значительно продвинет современную науку. Назвали их задачами тысячелетия и за решение или опровержение каждой из них готовы отдать 1 000 000$. Вот об этих задачах мы и поговорим.

Одна из задач, а именно Гипотеза Пуанкаре получила решение. Её доказательство предоставил, ставший в одночасье известный на весь мир математик Григорий Перельман в 2010-м году. Он куда круче Киану Ривза, потому что тоже может быть грустным и в одних джинсах, оставаясь всемирно известным, но в отличии от Нео Григорий на самом деле избран. От денег он отказался. Объяснив это следующим образом:

«Я отказался. Вы знаете, у меня было очень много причин и в ту, и в другую сторону. Поэтому я так долго решал. Если говорить совсем коротко, то главная причина — это несогласие с организованным математическим сообществом. Мне не нравятся их решения, я считаю их несправедливыми. Я считаю, что вклад в решение этой задачи американского математика Гамильтона ничуть не меньше, чем мой»

Хотя стоит заметить что Ричард Гамильтон от своей премии не отказался, и получил её в 2011 году. Это была премия Шао, которую многие знают как «нобелевская премия востока». В общем Ричард всё же забрал свой миллион долларов.

Но давайте мы с вами вернёмся к оставшимся шести задачам.

Равенство классов P и PN.

Наверно самая простая для понимания задача из списка. Допустим у вас есть уравнение:

2*х^2-11*х+5=0. Что проще, решить уравнение или проверить является ли число 5,5 решением? Согласитесь, что напрашивается вывод, что проверить вроде проще. Подставил 5,5 да решай, а чтобы найти корни, ещё нужно вспоминать дискриминанты. А вы сможете доказать, что проверить действительно проще чем решить? Если сможете, то у меня для вас отличные новости миллион долларов ваш! Потому что именно это и требуется доказать. Или же напротив доказать то, что и решение, и проверка, в общем случае требует одинаковых трудозатрат.

Данная задача частично касается и раздела формальной логики. Предположим, что вам известно, что все тиали одинакового цвета. На какой вопрос вам будет проще найти ответ: «Тиали зелёные?» или «Какого цвета тиали?».

Гипотеза Ходжа.

Сформулирована была без малого 80 лет назад, до сих пор ни доказана, ни опровергнута. Давайте попробуем разобраться в чем её суть. Предположим что у нас есть некоторое сложное тело свойство которого нам нужно изучить. Давайте возьмём модульный дом, к примеру. И вы чтобы изучить свойства всего дома изучаете свойства его составляющих – готовых модулей. Их то изучить проще. А кто-то скажет, а давайте будем изучать не модули, а то из чего они состоят – кирпичи, их то изучить ещё проще. А потом кто-то захочет изучать свойства песчинок, из которых состоят кирпичи. И так далее. Вот это самое разложение изучаемого объекта на кусочки попроще, называется аппроксимацией. И смысл гипотезы Ходжа в том, до какого уровня можно аппроксимировать сложные многомерные объекты простыми, со всё более увеличивающейся размерностью.

Гипотеза Римана.

Ну тут всё просто, потому что речь идёт о простых числах. Помните такие верно? Это те, которые делятся без остатка только на себя и на единицу. Ну например 2,3,5,7,13 (единица не входит, ибо простое должно иметь два делителя). До сих пор не известно есть ли механизм их появления в числовой последовательности натуральных чисел, или они располагаются хаотично в этом мире, но точно доказано что количество простых чисел бесконечно, и вы не поверите, но доказал это Эвклид 2300 лет назад.

С тех пор все кому не лень пытались, вывести закономерность их появления, и если у вас получится, то вам никакая гипотеза Римана не нужна. Ваше имя навеки останется в ряду с Эйнштейном, Ньютоном и Аристотелем. Но нам слава и известность не нужна, мы хотим всего лишь 1 000 000$. Его дают за доказательство гипотезы Римана, общий смысл сводится к нахождению количества простых чисел на заданном отрезке. Ну вот, например сколько простых чисел от 0 до 10? 2,3,5,7 получаем 4 простых числа. Так вот Риман вывел функцию, которая может в том числе посчитать сколько простых чисел встречается на отрезке. Её то и нужно доказать или опровергнуть.

Теория Янга — Миллса

В целом это математическая модель, которая описывает то, к чему так остервенело рвался Эйнштейн, теорию единого поля, с одной помарочкой. Давайте немного подробней. В нашей вселенной существует 4 вида фундаментальных взаимодействий. Про гравитационное и электромагнитное, каждый хоть раз слышал. Их описывали Ньютон и Кулон. А вот сильное и слабое взаимодействие проявляют себя только на расстояниях сопоставимых с размерами атомов, или и того меньших. Поэтому мы про них так мало знаем. И никак пока не придумают формулу, которая все эти 4 взаимодействия собрала бы в кучу. Эйнштейн бился, Тесла бился, да никак.

И вот Янг Чжэньнин совместно с Робертом Миллсом в 1954 году нашли способ описать три из четырёх этих взаимодействий. Гравитационное в их описание не попадает. Сперва их описания не воспринимались в серьёз, но далее всё больше и больше практических наблюдений сходилось с их теорией. И теперь институт Клэя готов отдать 1 000 000$ за доказательство или опровержения их формул.

Уравнения Навье-Стокса.

На мой взгляд самая интересная задача тысячелетия. Для начала возьмём уравнения движения классической механики. Они позволяет совершенно точно сказать, где будет находится тело в следующий момент времени. Вот тоже самое сделали Анри Навье и Джордж Стокс для течения жидкостей и газов. Их уравнения позволяют точно сказать, как будет вести себя поток жидкости или газа в последующий момент времени. Они надёжны, проверены временем и выведены около 200 лет назад в 1822 году. Но вот какая с ними загвоздка, в теории эти уравнения могут «сломаться» (или нет). И вот что я имею в виду. При некоторых начальных условиях, теоретически возможна такая ситуация, в которой скорость одной из частиц, описываемых уравнением, станет бесконечной. Ну и это не есть гуд, ведь грош цена уравнениям, когда в них приходится на бесконечность умножать или делить. Так вот смысл задачи тысячелетия сводится к доказательству того, что уравнения навье-стокса никогда не «ломаются». Ну или наоборот, продемонстрировать ситуацию, в которой это произойдёт. Эту задачу кстати пытаются решить чаще остальных из задач тысячелетия. Так, например, в 2014 году преподаватель из казахского университета Мухтарбай Отелбаев, предложил решение, но оно оказалось неверным.

Гипотезе Бёрча — Свиннертон-Дайера.

Её даже выговорить сложно и, пожалуй, самая сложная для понимания. (рекомендую посмотреть видео))))

Гипотеза, утверждающая некоторые особенности из жизни эллиптических кривых (не путать с эллипсом). В общем случае, для рациональных чисел, эти кривые имеют вид:

y^2=x^3+ax+b. За исключением пары коэффициентов. Выглядят эти кривые как на рисунке чуть ниже:

Ну и математики для них понапридумывали разные правила. Например, правила сложения точек между собой, и сложения точки самой с собой. Геометрический смысл последнего в том, что к точке нужно провести касательную, а затем посмотреть, где эта касательная пересекает кривую. Если вовсе не пересекает, то говорят об особой точке – бесконечной. (К ней кстати тоже можно что-то прибавлять или отнимать, и в результате не получится бесконечная точка, такие вот странные там правила сложения).

И вот было замечено что у любой эллиптической кривой есть такие волшебные точки, которую если неоднократно складывать саму с собой, то в результате придём к циклу. Т.е. если изначально была точка Р, а в результате операции n*Р – бесконечность, то (n+1) *Р слова даст просто Р. Ну и всё начинается заново по циклу, такие волшебные точки называются точками кручения. Так же подмечено что любую точку на изначальной эллипсоидной кривой можно представить в виде ряда Р=А1*Р1+А2*Р2+…Аn*Рn+Q. Где Q точка кручения, Аn- целые числа, а всякие Р – это просто точки на кривой, но подобранные особым образом.

Это то, что доказано и изучено, а вот неизученным остался вопрос минимальной длинны этого ряда (она, кстати, называется рангом эллиптической кривой). Точно известно, что ранг конечной длинны, но неизвестно как эту длину вычислить. Вот тут и приходит на помощь гипотеза Бёрча — Свиннертон-Дайера, она как раз и говорит о том, как вычислить ранг эллиптической кривой. Но пока гипотеза ни доказана ни опровергнута.

Я ни слова ни сказал о практической стороне дела. Ну просто потому очень много придётся говорить. Ведь из всего списка нерешённых задач по математике, именно эти 6 имеют наибольшее значение, а потому за них и готовы платить по миллиону долларов просто люди с улицы.

Спасибо что дочитали до конца)))