TuzimunMath

На дворе 1⁴+2⁴+3⁴+5⁴+6⁴ год, а ты до сих пор не знаешь, что такое сикус? Тогда тебе сюда https://pikabu.ru/story/sikus_trigonometricheskaya_funktsiya..., а если ты знаешь, что такое сикус, то читай дальше!

Теорема сикусов.

Пусть есть произвольный треугольник ABC со сторонами a, b и с и углами α, β и γ.

Тогда для него справедливо следующее утверждение:

(для других углов аналогично)

Доказательство:

По определению sic(α) = sin(α) + cos(α). Умножаем это равенство на 2bc и получаем следующее выражение:

И преобразовав его получаем формулу теоремы сикусов! (S - площадь треугольника)

Если вы не поняли почему 2bc*cos(α) = c² + b² - a², то смотрите теорему косинусов.

Если вы хотите, что бы я написал статью в википедии про теорему сикусов, то пишите в комментариях.

А так же настоятельно рекомендую узнать, что такое "Тосинус" и "Керсинус"!

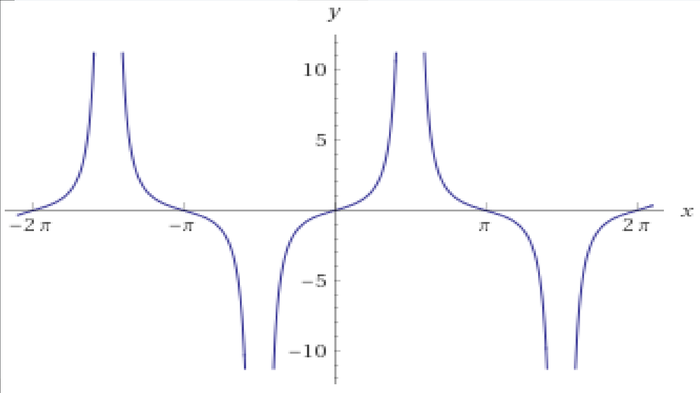
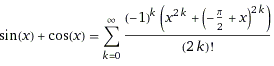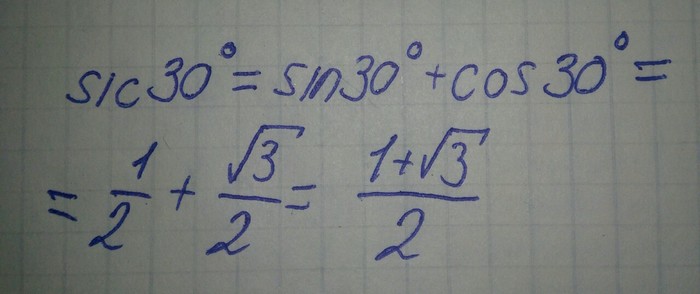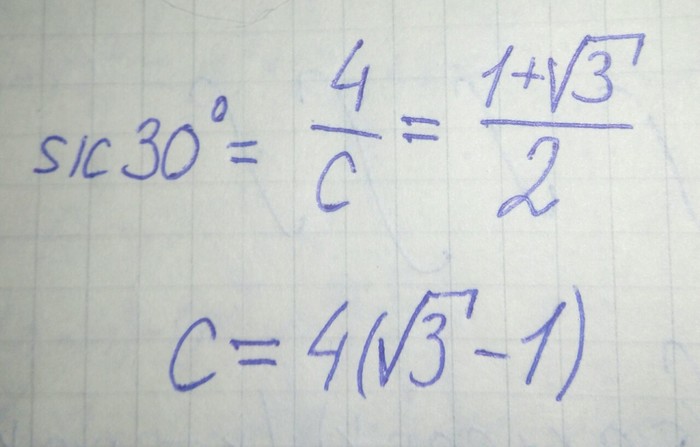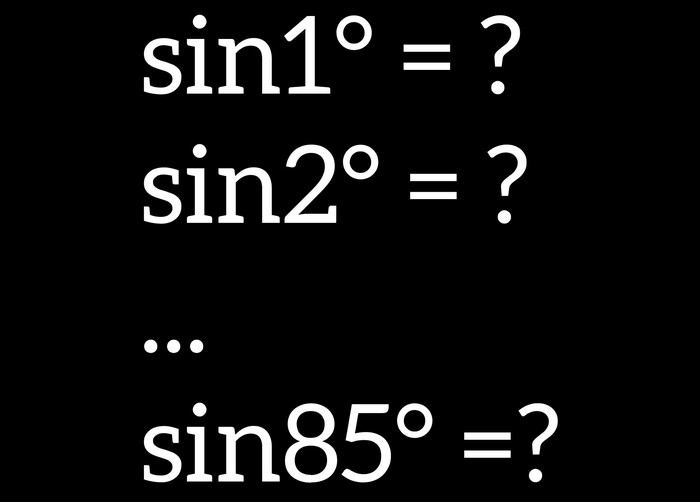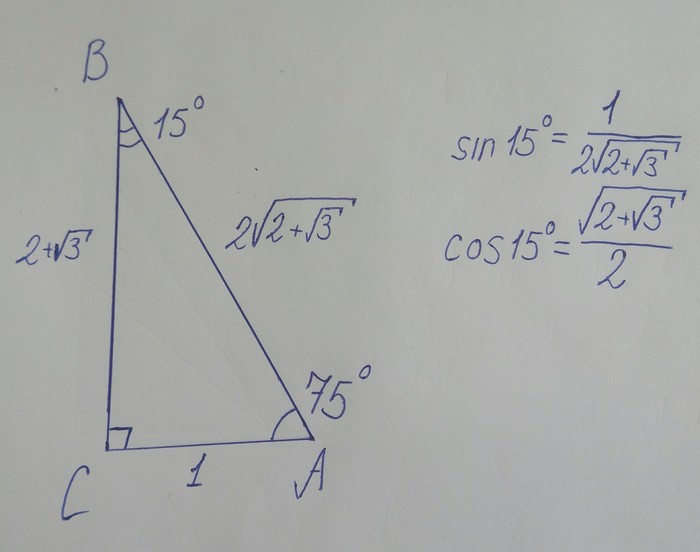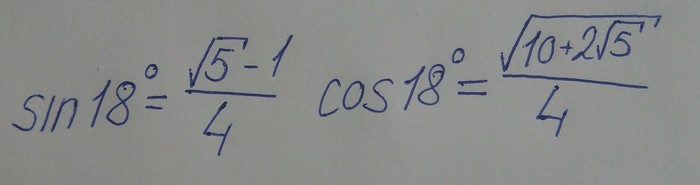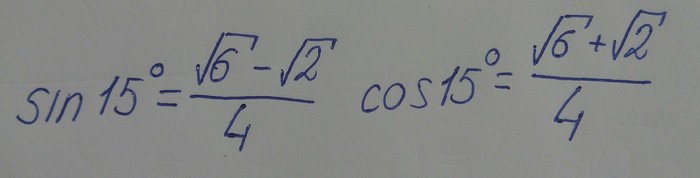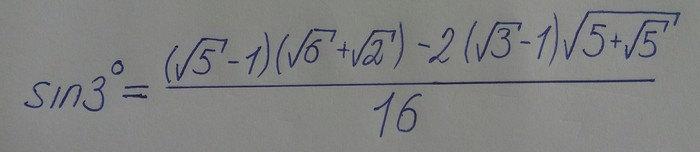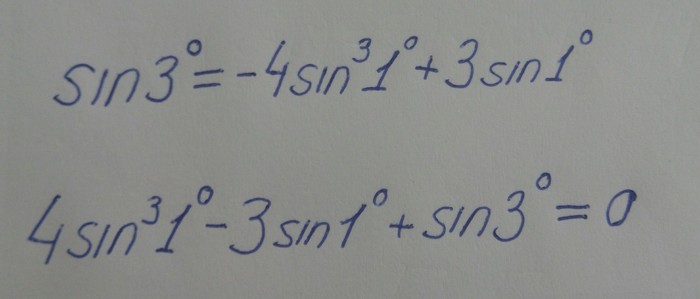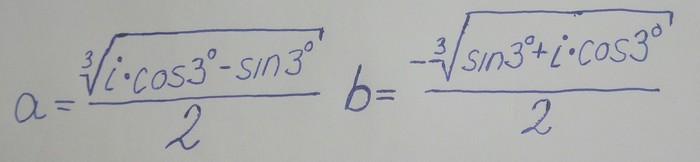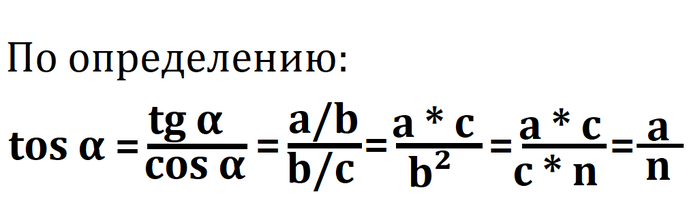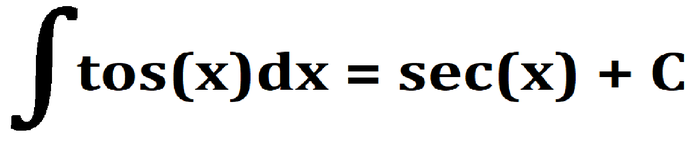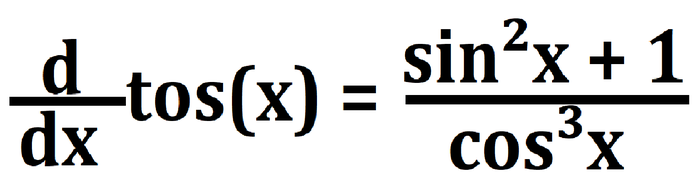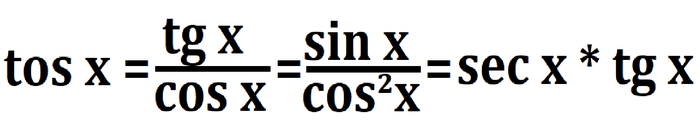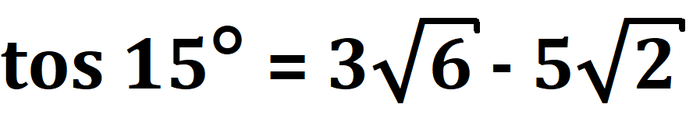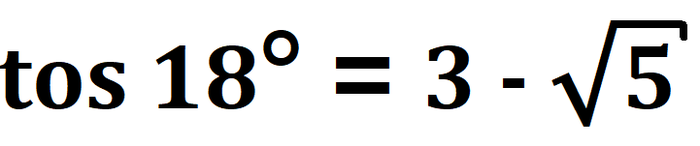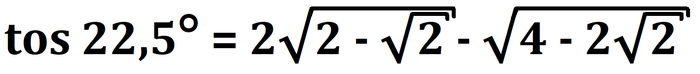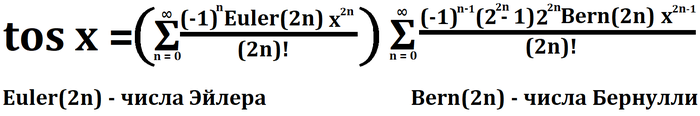Этот вопрос мучает меня с того момента, как мы начали изучать тригонометрию. И спустя чуть больше года я нашел способ!
Порядок действий:
1) Найти синус и косинус 15°
2) Найти синус и косинус 18°
3) Зная синусы и косинусы 15° и 18°, найти синус 3° (используя формулу синуса разности аргументов)
4) Зная синус 3°, найти синус 1° (используя формулу тройного угла)
5) Зная синус 1°, мы можем найти синус любого целого угла (используя формулы двойного, тройного и т.д. углов)

Пункт 1. Найти синус и косинус 15°.
Есть много способов искать синус и косинус 15°, самый простой из них - это синус/косинус половинного угла, но я буду выводить из прямоугольного треугольника. Такой способ, который я вам сейчас покажу, я нигде не видел (хотя долго искал), так что можно сказать, что он авторский ©.
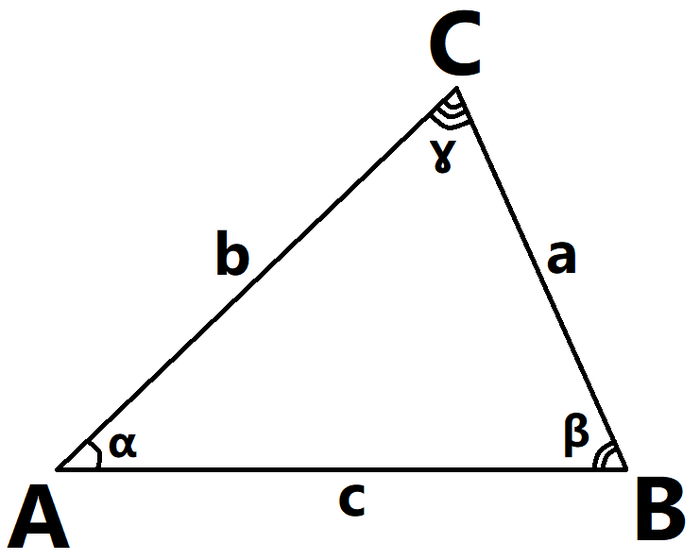
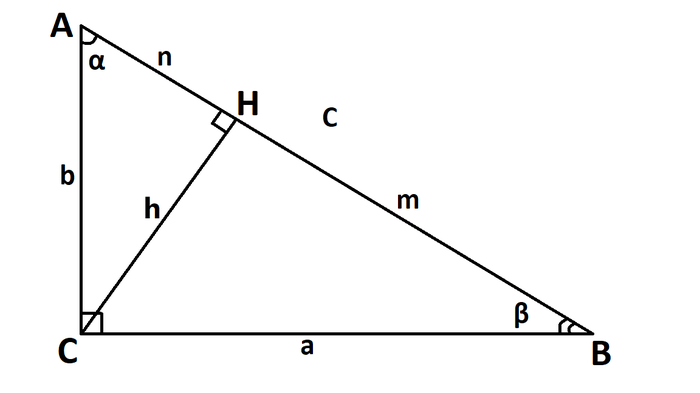
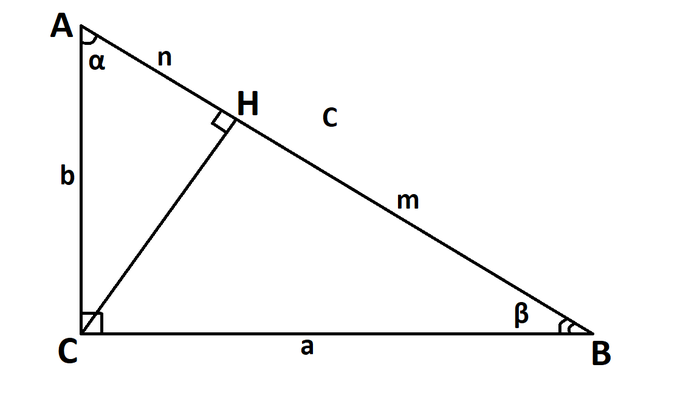
Нарисуем такой треугольник

Начнем с треугольника ACM. Пусть AC = 1.
Тогда: AM = 2, CM = √3.

Переходим к треугольнику AMB. Очевидно, что этот треугольник равнобедренный, значит: BM = AM = 2.
Заканчиваем треугольником ABC.
AC = 1, BC = MC + BM = 2 + √3. Мы знаем длины двух катетов, и необходимо найти гипотенузу. Искать будем по теореме Пифагора.

Нарисуем опять изначальный треугольник, только уже с известными сторонами.

Синус и косинус 15° успешно найдены!

Пункт 2. Найти синус и косинус 18°.
Тут я ничего вам авторского показать не могу, так что можете посмотреть видео как выводить синус 18°, а косинус можно найти из основного тригонометрического тожества

Не смотря на то, что видео не на русском языке там должно быть все понятно, а я буду использовать уже готовые значения синуса и косинуса 18°.

Пункт 3. Найти синус 3°.
Все вы знаете формулу синуса разности аргументов (я надеюсь).

В нашем случае α = 18°, а β = 15°. Говорить тут особо нечего, а просто писать и считать...
Для удобства я буду использовать следующие значения синуса и косинуса 15°.

(это тоже самое, что я вывел в П.1)

Тут даже сводить к общему знаменателю не надо, поскольку он и так общий. Сначала умножаем, потом вычитаем и в конце получаем выражение, на которое смотреть страшно!

Но если чуть чуть поиграться с этим выражением, то мы получим конфеточку.

Пункт 4. Найти синус 1°.
Будем использовать формулу синуса тройного угла

В нашем случае α = 1°.
Получаем кубическое уравнение относительно sin1° в каноническом виде.

Для удобства сделаем две замены, тогда наше уравнение имеет следующий вид:

Решая это уравнение, мы понимаем, что это уравнение имеет три действительных корня, и эти корни будут значениями синуса 1°, 121° и 241°.
Т.к.sin(3*1°)=sin3°, sin(3*121°)=sin363°=sin3°, аналогично для 241°
Другими словами, если x1, x2 и x3 - это корни, то х1 = sin1°, x2 = sin121°, x3 = sin241°. Как определить какой из этих корней будет синусом 1°? Все более чем просто! Стоит отметить, что
sin241° < sin1° < sin121°, а это значит, что если расставить корни в порядке возрастания, то sin1° будет по середине!
Как решать кубические уравнения я не буду рассказывать, а просто выпишу корни этого уравнения.

(косинус 3° находим по основному тригонометрическому тождеству)

Справка: i - мнимая единица (если кто то не знает)

Теперь задание самым бешеным математикам: избавиться от мнимой части (если извлечь кубические корни, то для х1 мнимая часть сокращается, а для х2 и х3 она сократится при умножении на i√3).
И расставить корни в порядке убывания или возрастания, все равно sin1° будет посередине. Я делать этого не буду, т.к. это страшно и долго, и вообще моя задача показать сам процесс, а не выполнить его полностью.

Пункт 5. Находим синус любого целого угла по формулам синуса двойного, тройного и т.д. углов!

Конец!

Если нашли ошибку или есть вопросы, то пишите в комментарии! А если хотите больше треша, то можете посмотреть два моих предыдущих поста про тригонометрию! (На первый пост не обращайте внимания, т.к. это была проверка как работает Пикабу!)
P.s. давайте соберём 100 плюсиков:)

Не надо обвинять меня в вандализме!
Тосинус — тригонометрическая функция, которая может возникнуть при рассмотрении прямоугольных треугольников и выражает зависимость длин сторон этого треугольника и частей гипотенузы, на которые её делит высота от острых углов. Эта функция не имеет широкого применения в науках, связанных с математикой.

Тосинусом угла α называется отношение a/n. (tos α = a/n).
Тосинусом угла β называется отношение b/m. (tos β = b/m).
Другими словами тосинус — это отношение тангенса угла к его косинусу.

График функции y = tos(x) имеет следующий вид:

Период функции 2π.
Функция имеет разрыв второго рода в точках вида 0.5π + πn, n ∈ Z.
Первообразная и производная тосинуса:

Основные тождества:

Значения тосинуса нестандартных углов

А теперь моё любимое, разложение в ряд Тейлора

Да, выглядит страшно... но это не важно.

Еще раз говорю, что не надо обвинять меня в вандализме! Имейте совесть! Лето на улице, а человеку нечем заняться, даже сделал сайт про тосинус http://www.perfect-math.top

Задавайте любые вопросы в комментариях!