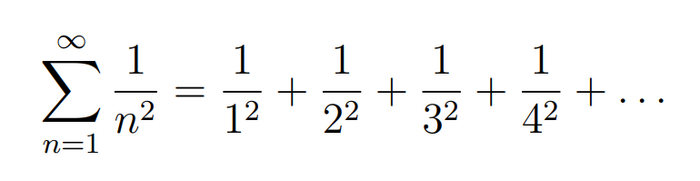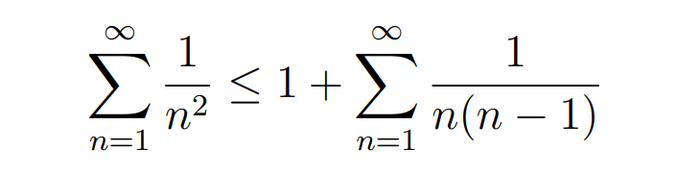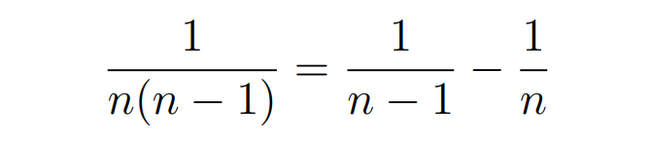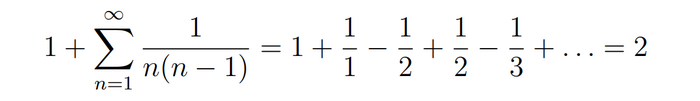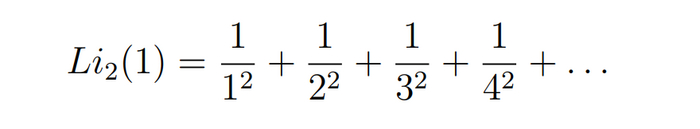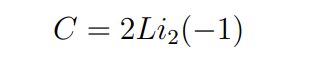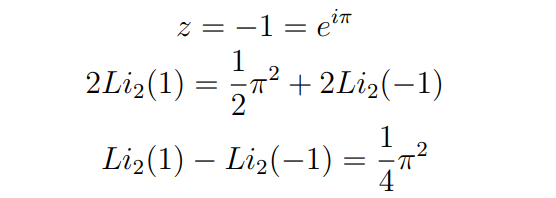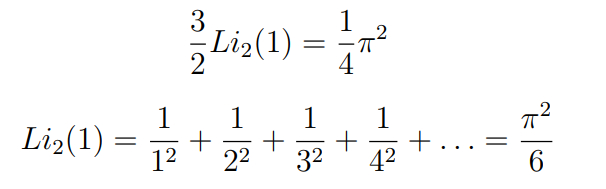Почему этот ряд вообще сходится?

Забавно, что если убрать квадраты в знаменателях:

то сумма не будет сходиться (больше любого числа или равна бесконечности). Последнее равенство означает, что сумма при больших n "ведет"(мало отличается) себя как логарифм, но доказывать я это не буду.

Однако сумма обратных квадратов -- сходиться.

Для того, чтобы показать, сто наша сумма сходится оценим ее сверху другим рядом, который сходится:

Видно, что все слагаемые нашей суммы, кроме первого меньше, чем у суммы справа.

Покажем, что ряд справа -- сходится. Для этого распишем каждое слагаемое, как сумму:

Тогда наша ряд слева принимает вид:

Видно, что эта сумма сходится. Так как сумма обратных квадратов не превосходит 2, то она сходится.

Дилогарифм

Для начала вспомним об одном важном свойстве логарифма, а именно его разложении в ряд:

В этом смысле дилогарифм похож на обычный логарифм. Он определяется как:

(это равенство, как и равенство выше верно также для комплексных z)

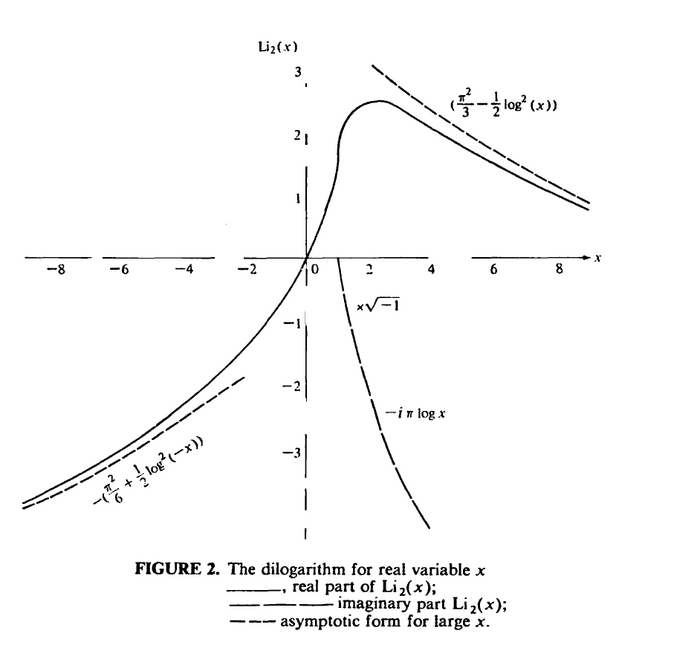
График для вещественных x выглядит следующим образом:

Заметим, что значение дилогарифма в 1 -- это в точности сумма нашего ряда:

Пора считать!

Для начала докажем одно важное свойство дилогарифма, а именно следующую формулу:

Для этого рассмотрим следующую производную:

Посчитаем то что справа:

А затем проинтегрируем:

Найдем C, подставив z=1:

Перенесем Дилогарифм от -z налево и получим нашу формулу:

Ура! Теперь дело за малым. Подставим z = -1:

(здесь все законно, так как комплексный логарифм определен и при отрицательных z)

Теперь надо вычислить(или выразить через дилогарифм от 1) дилогарифм от -1.

Следующие выкладки дают нам, то что нужно:

(важно отметить, что так как ряд сходиться абсолютно, то мы вправе переставлять и группировать слагаемые)

Подставим в нашу формулу и получим:

Также в процессе мы вычислили ещё одну сумму, а именно:

Примечание: подробнее про дилогарифм написано в книге "Leonard Lewin - Polylogarithms and associated functions (1981, North Holland )".