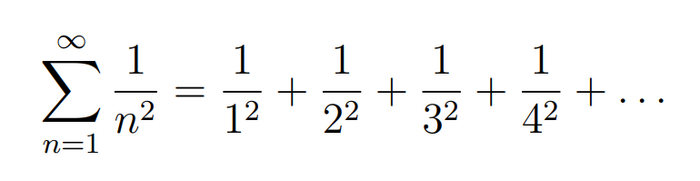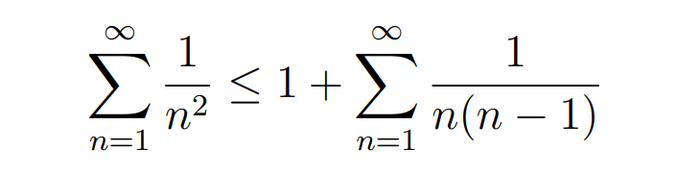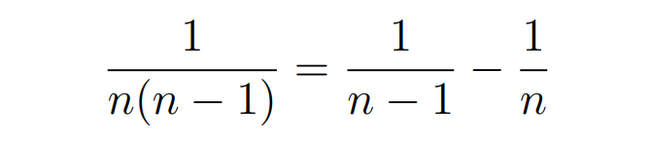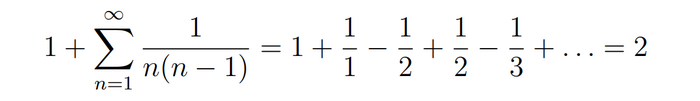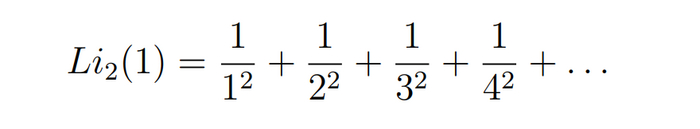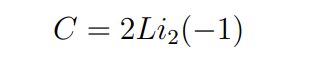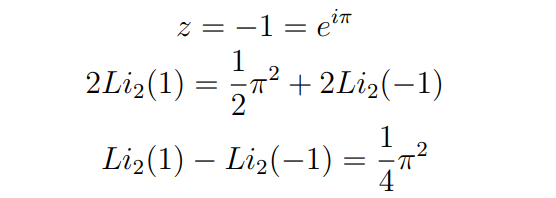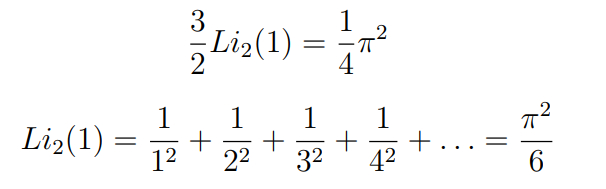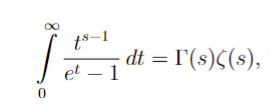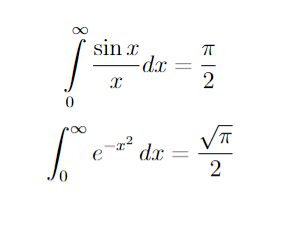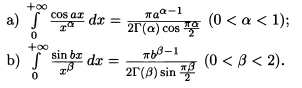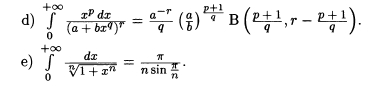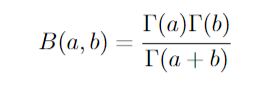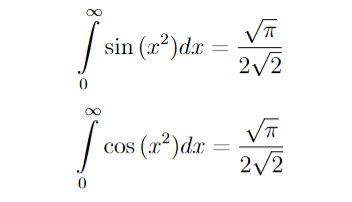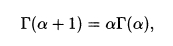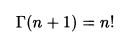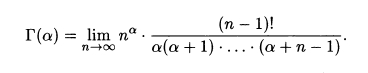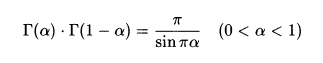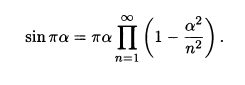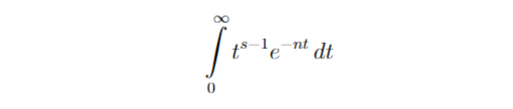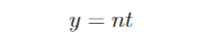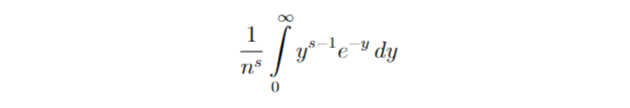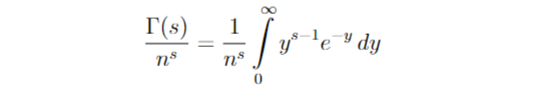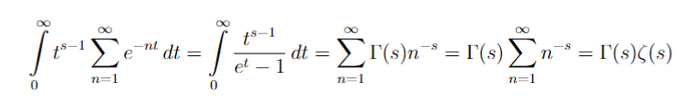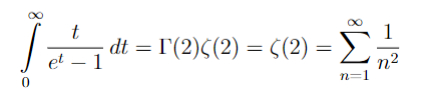StasTatarski

то сумма не будет сходиться (больше любого числа или равна бесконечности). Последнее равенство означает, что сумма при больших n "ведет"(мало отличается) себя как логарифм, но доказывать я это не буду.

Однако сумма обратных квадратов -- сходиться.

Для того, чтобы показать, сто наша сумма сходится оценим ее сверху другим рядом, который сходится:

Видно, что все слагаемые нашей суммы, кроме первого меньше, чем у суммы справа.

Покажем, что ряд справа -- сходится. Для этого распишем каждое слагаемое, как сумму:

Тогда наша ряд слева принимает вид:

Видно, что эта сумма сходится. Так как сумма обратных квадратов не превосходит 2, то она сходится.

Дилогарифм

Для начала вспомним об одном важном свойстве логарифма, а именно его разложении в ряд:

В этом смысле дилогарифм похож на обычный логарифм. Он определяется как:

(это равенство, как и равенство выше верно также для комплексных z)

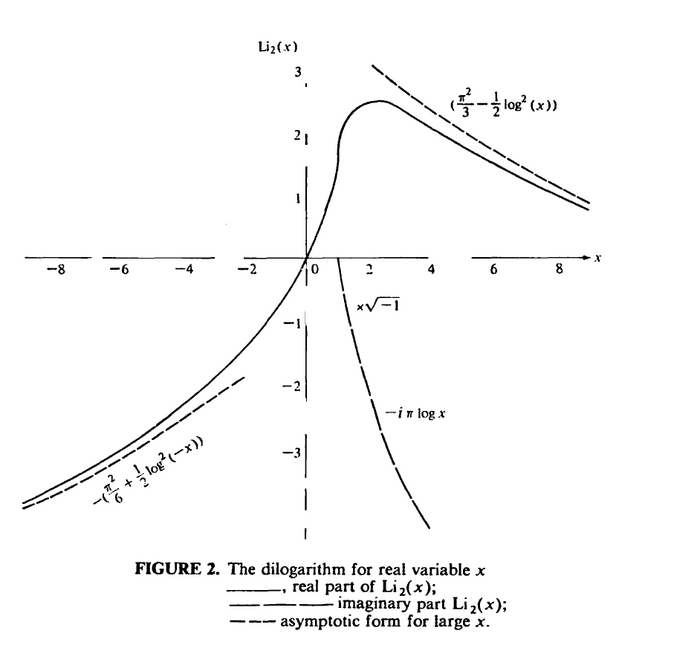
График для вещественных x выглядит следующим образом:

Заметим, что значение дилогарифма в 1 -- это в точности сумма нашего ряда:

Пора считать!

Для начала докажем одно важное свойство дилогарифма, а именно следующую формулу:

Для этого рассмотрим следующую производную:

Посчитаем то что справа:

А затем проинтегрируем:

Найдем C, подставив z=1:

Перенесем Дилогарифм от -z налево и получим нашу формулу:

Ура! Теперь дело за малым. Подставим z = -1:

(здесь все законно, так как комплексный логарифм определен и при отрицательных z)

Теперь надо вычислить(или выразить через дилогарифм от 1) дилогарифм от -1.

Следующие выкладки дают нам, то что нужно:

(важно отметить, что так как ряд сходиться абсолютно, то мы вправе переставлять и группировать слагаемые)

Подставим в нашу формулу и получим:

Также в процессе мы вычислили ещё одну сумму, а именно:

Примечание: подробнее про дилогарифм написано в книге "Leonard Lewin - Polylogarithms and associated functions (1981, North Holland )".

Введение
Сегодня я хочу рассказать об одной очень красивой формуле, связывающей дзета-функцию Римана и Гамма-функцию(не пугайтесь я все объясню). Формула выглядит вот так:

Также в процессе своего рассказа я хочу осветить такую тему, как специальные функции и рассказать для чего они нужны.

Специальные функции

1. Мотивация

Часто в задачах математики, физики и других естественных науках нам приходится иметь дело с интегралами, которые не приводятся к стандартным (таким как косинус, экспонента и т.д.). В этом случае весьма полезно знать некоторые "трюки", позволяющие преодолевать такого рода трудности. Одним из таких "трюков" является использование специальных функций.

Первое моё знакомство со специальными функциями произошло во время чтения первого тома Теоретической физики Ландау и Лифшица (Ландау Л., Лифшиц Е. Теоретическая физика. Т. I. Механика. М.: Физмат-лит, 2021 с. 41):

Как видно последняя подинтегральная функция имеет довольно простой вид, однако, так как этот интеграл не выражается через стандартные, приходится идти на различные ухищрения при его вычислении (я не буду приводить здесь вычисления, кроме объявленного интеграла, однако их можно проделать в качестве упражнения с указаниями в учебнике В. А. Зорича "Математический анализ Часть II" или в Демидовиче, к которому есть китайский решебник).

Также гамма-функция значительно упрощает вычисление таких классических интегралов, как интеграл-Дирихле и интеграл Пуассона:

Последний имеет важное значение в теории вероятностей.

Гамма-функция помогает при взятии многих других естественных интегралов:

1) Обобщение интеграла Дирихле

2) Похожие на тот, что был у Ландау

*Где В -- бета-функция Эйлера, которую можно определить равенством:

3) Интегралы Френеля:

2. Забавные свойства гамма-функции

1) Формула понижения

Доказательство проводится интегрированием по частям.

2) Г(1) =Г(2)= 1

Для доказательства Г(1)=1 продифференцируйте exp(-x), а потом проинтегрируйте справа и слева.

Для доказательства Г(2)=Г(1) проинтегрируйте Г(2) по частям.

3) Связь с факториалами

Сразу следует из (1) и (2).

4) Формула Эйлера-Гаусса

Доказательство этого и следующих фактов есть к книге Зорича, ссылка на которую есть выше.

5) Формула дополнения

Из этой формулы следует очень красивое разложение синуса, как произведения:

Обещанный интеграл

Рассмотрим интегралы вида:

Сделаем замену:

Получаем:

Заметим, что мы уже знаем чему равен этот интеграл. Это Г(s)! Значит:

Остается просто просуммировать по n и мы получим что что надо(формально говоря мы должны рассмотреть предел частичных сумм, а потом занести предел под знак интеграла, предварительно проверив, что функция под знаком интеграла--непрерывная).

Просуммируем убывающую геометрическую прогрессию под интегралом и получим нужное равенство.

Интересный факт

При s=2 получаем интересное равенство:

Однако, чтобы посчитать этот интеграл гамма-функции недостаточно и требуется более серьезная техника (в частности можно свести этот интеграл к другой специальной функции).