Что такое математика⁠⁠

Наверняка, у разных математиков, учителей, да и в принципе у всех людей своё понимание относительно того, что же такое «математика» и зачем она нужна.

В посте изложу исключительно своё мнение на этот счёт.

Иногда кого-то спрашивают: «зачем нужна математика?» и те зачастую отвечают: «ну вот, например, посчитать сдачу в магазине», «чтобы уметь считать зарплату и свои затраты» и т.д.

В этих ответах есть несколько проблем.

Первая: для этих вещей математика как таковая вообще не нужна. Для этого нужна арифметика. Операции уровня вычесть/сложить/умножить/разделить изучаются взрослым человеком и без обучения этому в школе. А при необходимости человек может изучить эти операции за несколько минут/часов с нуля. Но математику в школе учат на протяжении одиннадцати (ну ладно, иногда девяти) лет. Явно же, что не для того, чтобы уметь считать сдачу и коммунальные платежи.

Вторая: в современном магазине уже в принципе отпадает необходимость что-то считать при оплате картой.

Значит ли это, что отпадает необходимость в изучении математики и в будущем детей вообще не будут ей обучать?

Конечно же нет.

Более того, можно не уметь быстро (и даже, возможно, правильно!) считать в уме сдачу, ошибиться со счетом и при этом быть крутым математиком. Сам много раз видел примеры, когда чудовищно трудную задачу решают безумно красиво, разрывают её как Тузик шапку, а в конце допускают какой-то дикий ляп со сложением.

Всё почему? Математику интересен процесс поиска решения. Решить то, для чего не существует готового отработанного алгоритма (либо он неизвестен решающему). Когда это решение найдено и осталось дело за тем, чтобы сложить несколько чисел, интерес уже пропадает, «запала» нет. Скучно.

Более того, например, решить квадратное/кубическое уравнение, построить график функции, вычислить интеграл, производную «простой» функции — это тоже не математика. Потому, что для всего этого УЖЕ есть алгоритм. Всего-то нужно взять этот алгоритм и подставить туда нужные данные.

Иногда кого-то говорит, что математика в жизни ему ни разу не пригодилась. Толку было учить дроби, корни, степени, логарифмы, интегралы, функции и прочий бесполезный бред.

Всё верно, все эти «страшные» термины забываются большинством после окончания школы, кем-то сразу после сдачи контрольной работы, а кем-то после того, как закончен урок.

Так зачем мучить детей тем, что им в жизни «никогда не пригодится»?

Дело лишь только в том, КАК учить и как к этому подходить. Если обучать путем зубрежки типа: «запомни это правило, нужно делать так, чтобы получить правильный ответ», «вот формула для нахождения корней квадратного уравнения», «запомни, сумма углов равна...», «запомни, чтобы сложить дроби нужно...», «запомни эти формулы сокращенного умножения: квадрат суммы равен квадрату первого плюс удвоенное произведение плюс квадрат второго» и тд, то это тоже что угодно, но только не математика. Чем прекрасна математика и чем она в корне отличается от других наук — в ней кардинально мало информации, которую нужно зубрить и запоминать, что бы ни говорили (в следующих постах постараюсь привести примеры, как понимание сути позволяет значительно разгрузить память и исключить заучивание большого количества информации).

Математика — это «эльдорадо» для людей с плохой памятью. Если в химии, биологии, иностранных языках, истории всё держится на запоминании информации (это — основа), то в математике это уже вторично. Я, обучаясь в школе никогда специально не учил правил математики, не запоминал ни одной формулы. Более того, даже сейчас преподавая математику, могу сразу не написать готовую формулу для чего-то. Это — не важно. Запоминание часто приходит уже само собой после неоднократного применения в решениях. А если не приходит — это не страшно.

Обучение математики должно строиться не на принципе «запомни/выучи», а на принципе «а почему так?». Вот формула. Это всё понятно, но неинтересно. А вот откуда она взялась? Почему она именно такая? Как первый математик додумался до того, чтобы так всё упростить? Как он рассуждал, что представлял? Это же безумно интересно, как он сумел это посчитать тогда, когда еще НИКТО не знал, как это делается!

Вот пример:

Площадь круга равна пи*р^2. Это еще не математика.

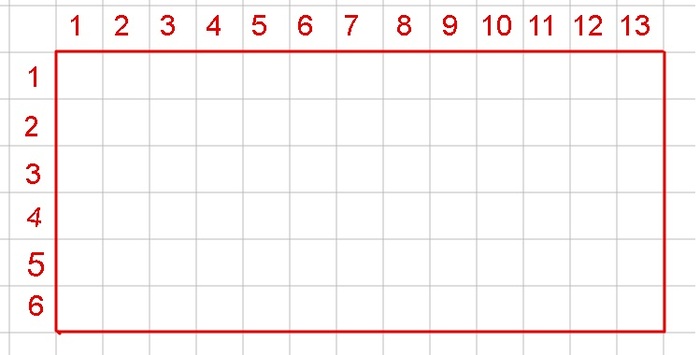
А как вообще додумались, как же посчитать площадь круга? (Так, а что такое площадь? Это количество «квадратиков» в фигуре). Если с прямоугольником тут всё просто, ведь если мы хотим посчитать количество клеточек в прямоугольнике, мы посчитаем сколько клеточек умещается в длину, а сколько в ширину, и потом умножим эти числа друг на друга. Вот и получим формулу площади прямоугольника: длину умножить на ширину.

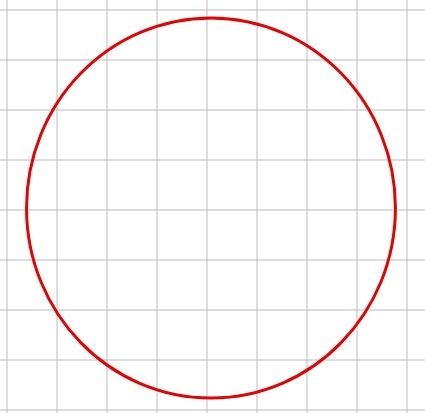
То как быть здесь с кругом?

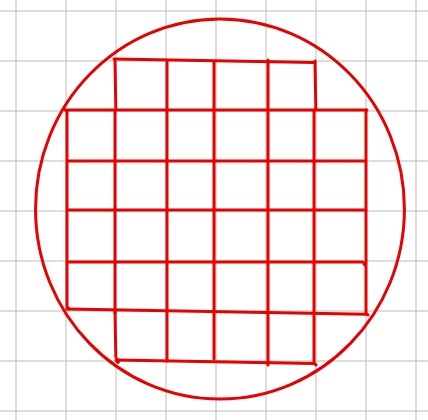
Ну хорошо, какие-то квадратики помещаются целиком, их мы посчитаем либо вручную, либо представим, что внутри окружности несколько прямоугольником умещаются и будем считать их площади.

А как быть дальше? Что делать с «откусанными» квадратиками? Могли бы и эти кусочки как-то друг с другом сложить, но ведь даже непонятно, какая часть от квадратиков осталась.

Всё, тупик?

Для большинства да. А ведь до нашей эры не было интернета, чтобы найти ответ (хотя, как знать? Ведь если не было найдено ни одно интернет-кабеля, это не означает, что интернета не было. Это только значит, что он мог быть беспроводным).

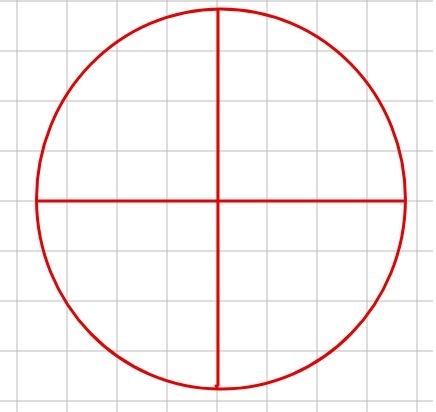
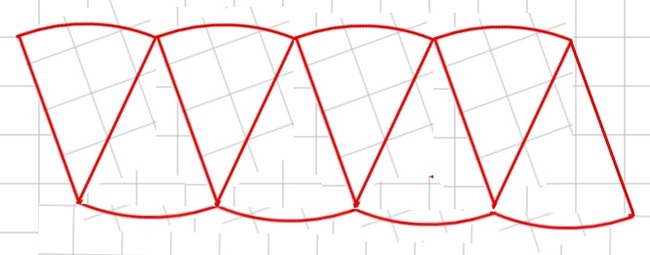
И вот один мужик придумал: а что если разрезать круг на четыре сектора:

А потом сложить их обратно в другом порядке:

Хммм… Ни*уя не понятно, но очень интересно. Но легче не стало. Так, а если разрезать на 8 частей и так же сложить?

Таааак. А 16? А 32?

И если мы разобъем окружность на бесконечно большое количество секторов, рано или поздно наша картинка будет очень близка к обычному прямоугольнику! Длина этого прямоугольника — это сумма этих маленьких дуг наших секторов. А так как снизу и сверху таких секторов ровно половина от общего количества, то суммарная длина этих дуг это половина длины окружности (а ее уже умели вычислять, длина равна 2*пи*р), а ширина прямоугольника — радиус нашей окружности. И что имеем для нашего прямоугольника? Площадь равна пи*р*р, то есть пи*р^2! (Блин, в таком написании выглядит так, будто я слово «пидр» замазал звездочкой.) Кстати, школьники, вот вам и мнемоническое правило для запоминания. Надеюсь, никто не сочтёт за пропаганду непотребностей среди несовершеннолетних.

Так вот, это я к чему. Математика — это не про посчитать числа. Математика — это про то, как думать, чтобы прийти к решению. А все числа и действия в математике — это всего лишь инструмент, топливо, на котором работает механизм рассуждений. Именно так строится обучение математике в хороших школах.

Даже если Вы отъявленный гуманитарий и не дружите с числами, то на уроках математики что-то да и должно отложиться в плане того, как строится взаимодействие между числами, какие логические цепочки применяются, как они работают. Как выстраивается четкая логика и уделяется внимание каждой точке, каждому значку. Ничего не берется из ниоткуда и никуда не пропадает.

И именно всё это и можно применить в своей жизни дальше, и числа, интегралы, дроби здесь ни при чем.

Математика учить думать, рассуждать.

Это как если бы боксер сказал: "Ну не знаю, мне ни разу на ринге не пригодилась скакалка и штанга, хз зачем я ими на тренировках занимался".

Почему я вообще полюбил именно математику? Я в детстве зачитывался детективами: Артур Конан Дойл, Рекс Стаут. И мне очень нравились рассуждения сыщиков, как они здорово выстраивают логику рассуждений, исключают маловероятное, делают допущения, проверяют их и в конце концов побеждают. А потом я всё это увидел на уроках математики. Там было всё то же самое! Только с числами.

Уже потом я увидел математику везде. Она окружает нас во всех сферах. Музыка - очень яркий пример этого.

Наверняка, кому-то известна и следующая аналогия: нужно в прямоугольник вместить несколько квадратов различного размера (по несколько штук каждого вида)

Так вот, что произойдет, если мы начнем в прямоугольник помещать сначала самые маленькие квадраты в случайном количестве в случайные места? Затем возьмем квадраты побольше и поместим их также в случайном количестве в свободные промежутки. То конечно, рано или поздно, почти наверняка окажется, что большие квадраты уже никуда не влезут даже при наличии большого количества свободных мест. Подход математики в том, чтобы начать заполнять прямоугольник большими квадратами, а в оставшиеся места помещать всё меньшие и меньшие, и всё поместится при полном заполнении прямоугольника. .

Так и с нашим временем. Если наше время мы начинаем занимать бесполезными вещами (телевизором, играми, просмотром мемасиков, соцсетями, сёрфингом в интернете), затем пытаемся в оставшееся время вместить туда чтение книг, работу, то на отдых и родных уже времени не останется.

С помощью математики можно найти выход из трудной жизненной ситуации, с помощью нее можно решить загадку, предсказать поведение, обнаружить обманщика (привет раздел логики), увидеть противоречия и т.д.

Поэтому, если кто-то не любит математику, то это потому, что Вас обманули и подсунули что-то другое вместо неё.