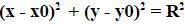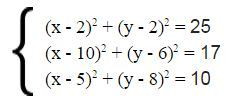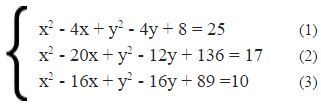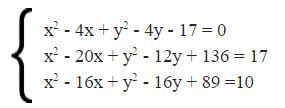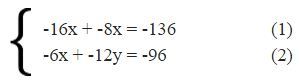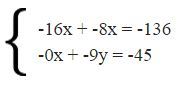Немного предыстории

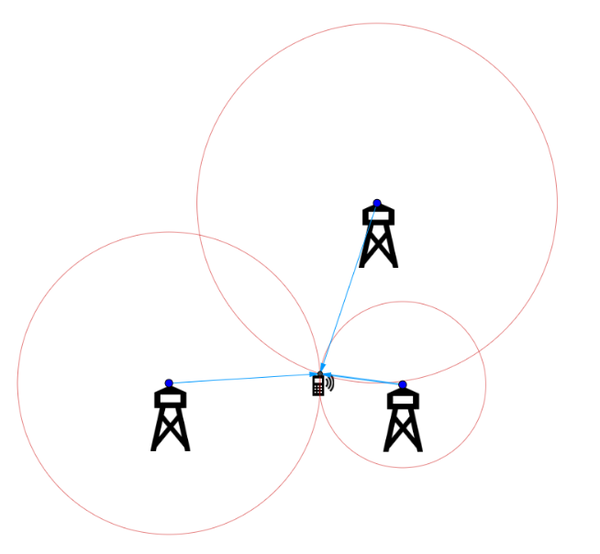
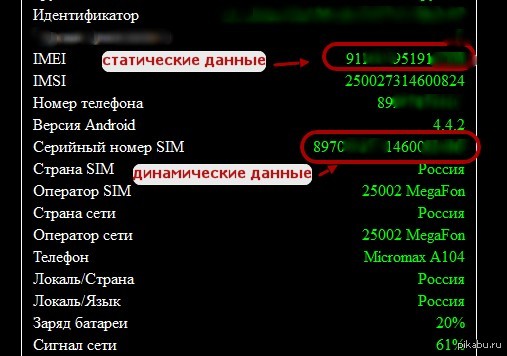
В начале ноября 2015 года я думал над проблемой триангуляции. Это когда находят местоположение точки на основании информации о расстоянии до неё. Самый лучший пример - это мобильный телефон и три радио-вышки

Может показаться что у трёх окружностей может быть лишь одна точка пересечения. Но не совсем. Не всегда окружности оказываются идеального размера и пересекаются в одном месте. В таком случае их не будет(для всех трёх сфер), или же точки пересечения будет 2, если окружности лежат на одной прямой.

Заметив постановку задачи вы должны были возмутиться. Мол, “Как же так? Мы ведь живём в трёхмерном пространстве, а ты задвинул какую-то туфту с двухмерной моделью”.

Спокойно. Сейчас всё будет.

Давайте рассмотрим решение этой задачи в 2D.

Как описать окружность? Школьная геометрия. Отталкиваясь от неё давайте анализировать, а не тянуться за учебником.

Для начала спросим себя, а из чего она состоит(этот вопрос мы будем задавать еще очень много раз)? У окружности есть: координаты её центра(x, y), и радиус(r).

Ну ладно, а дальше-то что делать? А то что мы можем описать её в некой системе координат (читай - плоскости).

Общая формула уже давно известна и проверена. Её и выпишем:

где x и y - неизвестные, x0 и y0 координаты центра окружности, а R - радиус.

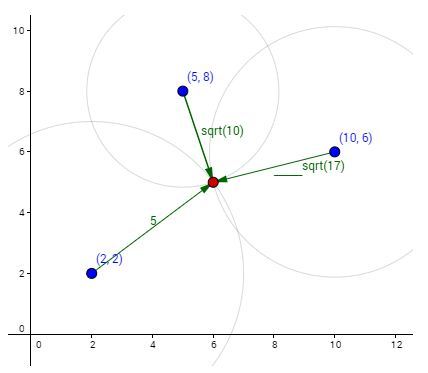
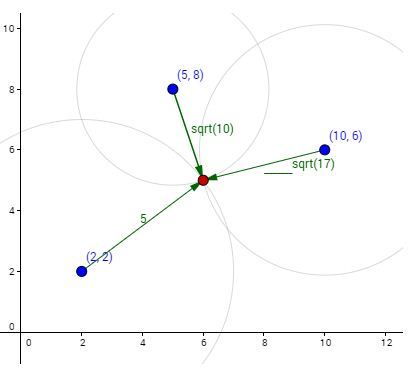
Привожу как пример уже проанализированную мной задачу.

А зачем оно вам нужно? Что бы понять ход моих мыслей, и то как решить эту задачу.

Зная координаты наших точек и расстояние до искомой - составляем систему линейных уравнений. Вспоминаем общий вид формулы окружности

Раскроем скобки и обозначим уравнения (1), (2), (3).

Обратите внимание на квадраты. Сейчас мы от их избавимся, что бы была возможность решить СЛАУ методом Гаусса.

Так как у нас в системе 3 уравнения с двумя неизвестными - можно вычесть любое уравнения из оставшихся двух. Сделаем это с первым и приравняем его к 0 для удобства счёта

x2 - 4x + y2 - 4y + 8 = 25

=

x2 - 4x + y2 - 4y - 17 = 0

x2 - 10x + y2 - 12y + 136 = 17 ← Вычтем из 2-го уравнения первое

x2 - 4x + y2 - 4y - 17 = 0 ← Вот это

-16x - 8x + 153 = 17 ← Результат

Делаем такую же операцию с третьим уравнением и получаем преобразованную систему

Искушенный читатель уже наверняка заметил что можно сократить уравнение и посчитать руками. НО МЫ ТАК ПРОСТО НЕ СДАЁМСЯ!

Давайте решим методом Гаусса :3

* Небольшое отступление. Наверное я прикреплю ссылку на свою программу, которая решает эти задачи *

Считаем определитель первого множителя. a1 = 6/16.

Создаём уравнения для вычитания.

-6x + -3y = -51

Произведём первый раунд операций над матрицей.

Так как у нас система размерностью 2, то и решилась она за первый раунд преобразований.

На выходе получили решённую матрицу. Считаем корни.

y = -45 / -9 = 5

Подставляем в первое уравнение найденный корень

-16x + -40 = -136

-16x = -96

x = -96 / -16 = 6

Ответ: x = 6; y = 5;

Похоже на правду? Еще бы. Это поиск точки по пересечению окружностей. Кстати, Этот метод позволяет решить систему с небольшой погрешностью. Так что даже если окружности не пересекаются, то вы всё равно получите приблизительные координаты.

На 100 000 тестах максимальной погрешностью было 10 в -12-й степени, что является достаточно низким показателем для того что бы утверждать что этот метод решения близок к идеалу.

Возвращаясь к вопросу о том что эта задача построена на плоскости.

Немного подумав мы можем понять что существует решение и для пространства, и оно должно быть таким же.

Как бы не так.

Да, действительно в пространстве можно построить три сферы, вот только лишнего уравнения для того что бы убрать квадраты у нас не будет, так как в 3-х мерном пространстве используются 3 координаты, а значит у нас будет 3 неизвестных в системе с 3-мя уравнениями.

Что же делать? Варианта 2:

1. Трилатерация.

Страшная штука. Мне не хватило мозгов что бы разобраться что к чему, так что я перешёл к варианту 2(кстати, он и используется в системах геопозиционирования (читай - GPS).

2. Ввести еще одну сферу в систему.

И действительно, а почему бы и нет? Ведь мы ничего не теряем и не нарушаем целостность. Запомните этот момент.

Расписывать решение такой системы я не буду, но оно почти ничем не отличается от 2D, просто на 1-ну переменную больше.

На пока с этим всё. За вторую часть я попытаюсь рассказать как это поможет понять четырёхмерные измерения. Надеюсь, хоть кому либо это было интересно.