Эксель и НОД
Делал по работе таблицу с концентрациями вещества. Мне нужно было получить колонку с пропорциями и использовал в экселе функцию НОД (наименьший общий делитель, если кто не знает).
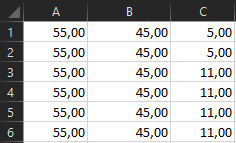
Столкнулся с вот таким интересным явлением (это уже не мои вычисления а попытка разобраться в ошибке с концентрацией 55%):
Чудесно, не правда ли? В какой-то момент эксель перестаёт адекватно воспринимать полученное в вычислении число и возвращает феерический результат.
Мне уже стало совсем интересно и я решил прогнать расчёт от 1 до 100%.
Чтобы не городить сложных формул, я делал промежуточные решения в столбцах. Так легче отследить ошибку.
И вот когда я на это посмотрел... я был удивлён.
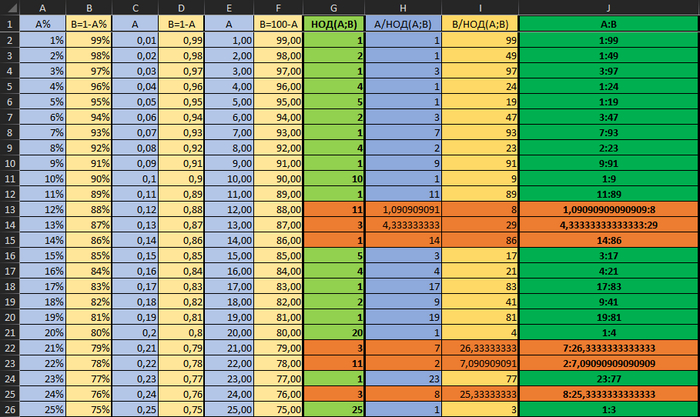
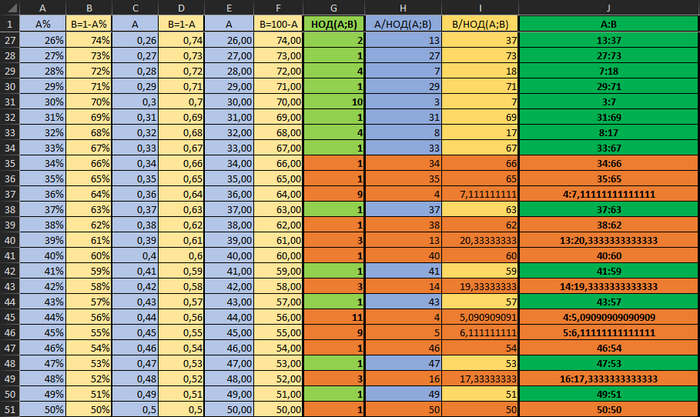
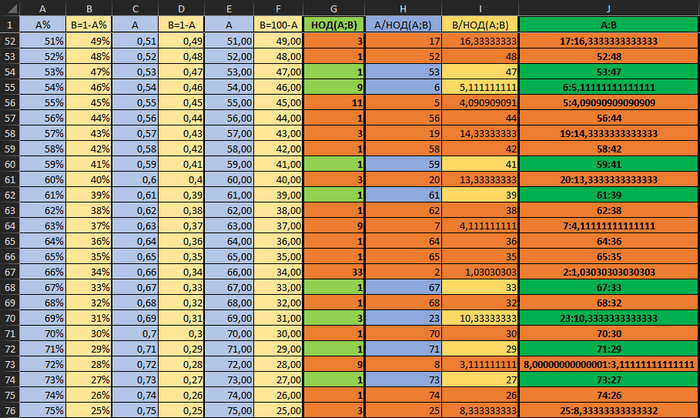
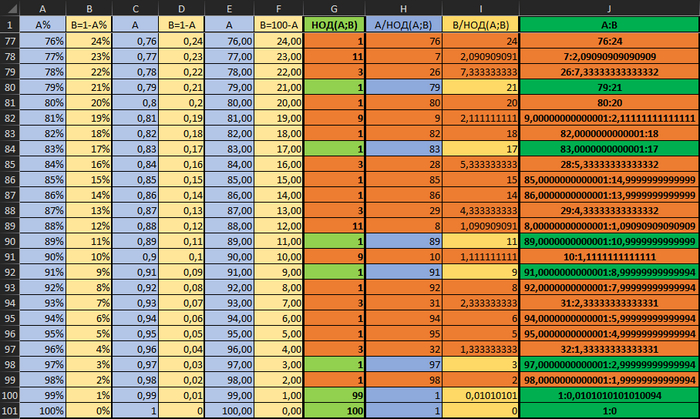
Это значения (с формулами можно ознакомиться в файле по ссылке). Оранжевым я выделил ошибки.
Из всего этого ряда мне изначально нужно было всего 20 значений. Но посчастливилось поймать ошибку и я полез разбираться.
На первый взгляд кажется, что у экселя проблема с простыми числами. Но нет, он даже для чётных чисел после 2-3 вычислений не способен выдать результат. У чётных чисел НОД = 1.
Более того, стало заметно, что точность операций с плавающей запятой - непредсказуема.
Например, НОД (20;80) он считает верно, а НОД (80;20) - уже не может. Хотя результат должен быть одинаковый.
Получается, что алгоритм вычисления НОД очень чувствителен и перед ним надо числа округлять до целых.
Используется Excel 2019. Вот прилагаю файл, если кому интересно:
https://docs.google.com/spreadsheets/d/16RMazU_jAGKAg3UHpIYL...
У кого есть возможность проверить формулы в своём экселе - какой результат покажет вам?
В комментариях указывайте версию своего экселя (или офиса).