Ответ на пост «Немного?»2
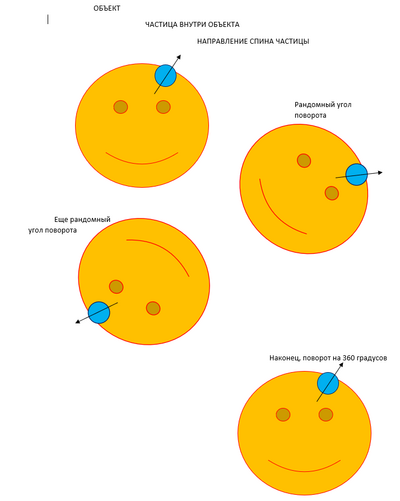
Уильям Гамильтон в середине XIX века занимался алгебраическим описанием поворотов трехмерного тела в пространстве. Самого обычного геометрического тела, без изысков, такого как шар, например. Для решения этой задачи, помимо всего прочего, он придумал кватернионы. Но что бы он не делал, всегда натыкался на странную особенность. Алгебраические уравнения, описывающие поворот тела возвращаются к исходному виду только после поворота на 720°, а не на 360°, как, казалось бы должно быть. Гамильтон так и не смог понять что это за чертовщина, и решил, что ну ладно, 720°, так 720°, вот такая странная математическая особенность. Ошибок в своих уравнениях он не нашел и оставил всё как есть.
А теперь перенесемся в наше время. Согласно современным представлениям физики, при повороте на 360° волновая функция частицы с полуцелым спином (например, электрона, протона, нейтрона) меняет знак: ψ -> -ψ (изменяется фаза волновой функции).
То, что сначала Гамильтон открыл чисто математически, потом получило объяснение в физике и было подтверждено рядом экспериментов. Поворот тела на 360° не возвращает его в исходное состояние, как кажется. Полный поворот достигается только поворотом на 720°.


ADME
2.4K пост3.2K подписчиков