Мифы о Золотом сечении
В одном из постов я рассказывал о том, что такое золотое сечение. Его идея настолько красива, что стала очень популярной ещё сотни лет назад и остаётся такой до сих пор. За это время она обросла мифами, а люди попытались найти заветное золотое соотношение даже там, где его нет
При написании прошлого поста я наткнулся на статью, опровергающую некоторые популярные мифы. Этот пост — её пересказ с небольшими дополнениями. Автор оригинальной статьи — Джордж Марковски, PhD по математике из Гарварда
Миф 1. Термин «Золотое сечение» использовался в античности
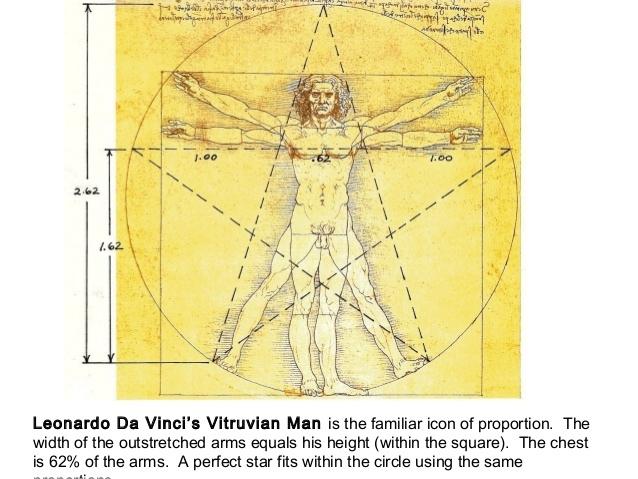
Многие считают, что знакомый нам сегодня термин был известен и в Античности, и у Леонардо да Винчи (одним из мифов является также то, что знаменитый художник и изобретатель использовал его в своих работах)
Пятиконечная звезда содержит золотые пропорции. Во славу математике, конечно
Но впервые термин в таком виде (разве что, на немецком) появился в 1835 году в книге Мартина Ома, брата знаменитого физика Георга Ома. На английском языке популярное сегодня название было впервые напечатано в 1875 году в Британской энциклопедии
Проблемы с измерениями
Часто золотое сечение находят в знаменитых памятниках архитектуры — египетские пирамиды, Парфенон. Иногда авторы таких открытий рисуют золотые прямоугольники, игнорируя части объекта, не придерживаются какой-либо стандартной методологии или чистоты критериев. Неудивительно, что так им удаётся обнаружить искомое соотношение. На иллюстрациях можно заметить, что углы, с которых сделано фото и границы прямоугольников сильно отличаются:
Измерения реальных объектов всегда могут быть только приближениями. Но, если допустимая ошибка в измерениях составит ±1%, то ошибка соотношения будет составлять уже ±2%! Для инженеров-строителей рекомендовано придерживаться интервала ±0,2%, но в оригинальной статье автор принимает допустимой ошибку измерения ±1%, то есть интервал [1,58; 1,66] для золотого соотношения φ
Но одно лишь попадание соотношения сторон в этот интервал не значит, что φ запланировано внесено в конструкцию. Это лишь первый тест, означающий, что имеет смысл исследовать ситуацию дальше
Миф 2. Великие пирамиды разработаны так, чтобы соответствовать φ
Многие люди находили φ в Великой пирамиде Хеопса, построенной за 2500 лет до нашей эры. Согласно одному из источников, длины сторон основания пирамиды варьируются от 755,43 футов до 756,08 футов, так что оно не является идеальным квадратом. Средняя длина — 755,79 футов. Высота указана равной 481,4 фута
Некоторые авторы утверждают, что Великая пирамида спроектирована так, что высота наклонной стороны относится к половине длины основания, как φ. По теореме Пифагора находим неизвестную сторону — она равна 612,01 футов
Это отношение действительно отличается от φ всего на 0,1%! Значит, имеет смысл провести более глубокое исследование
Гипотеза о нахождении φ в Пирамиде подтверждается словами древнегреческого историка Геродота. По его словам египетские жрецы сообщили ему, что размеры Великой пирамиды были подобраны так, что площадь квадрата, сторона которого была равна высоте пирамиды, равнялась площади треугольника стороны
Из этого утверждения выводится уравнение, решением которого действительно является φ. Проблема с опорой на утверждения Геродота в массе явных ошибок по отношению к описанию пирамид. Так, он указывает, что высота пирамиды, как и сторона квадрата в основании равнялась 800 футам. Но это не соответствует действительности ни сейчас, ни в прошлом. Также стоит заметить, что Геродот описывал Пирамиду через 2 тысячелетия после того, как она была построена
Так выглядит пирамида сегодня
Таким образом, эта гипотеза имеет мало смысла. Непонятно также, почему Египтяне хотели бы построить пирамиду именно таким образом, и неизвестно, знали ли они число φ — оно почти не встречается в других их строениях
Миф 3. Греки использовали φ в Парфеноне
Парфенон был построен в 5 веке до нашей эры. Многие прикладывают золотой прямоугольник к его фасаду, утверждая, что он идеально подходит. Однако, этих людей почему-то не смущает, что части здания выходят за пределы прямоугольника! Обратите внимание на ступени снизу и выступающие углы сверху:
Измерения Парфенона значительно отличаются у разных авторов, потому что каждый проводит их из разных точек. С таким широким разбросом данных энтузиаст может выбрать, какие удобно ему для получения лучшего результата
Например, одни авторы определяют высоту здания равной 45 футам и 1 дюйму, ширину — 101 футу, длину — 228 футам и 1/8 дюйма. Точки, между которыми проводились измерения не указываются. Но даже при этом отношение ширина/высота = 2,25 = 9/4, и длина/ширина = 2,25 — далеко за пределами допустимого интервала для φ. Можно предположить, что пропорции здания попросту отмерены в соотношении 4:9. Но другой автор приводит высоту, равной 59 футам. Тогда отношение ширины к высоте равно 1,71, что также не совпадает с золотым сечением.
Многие стремятся окутать мистицизмом древние строения, найти в них такие константы, как φ или π. Иногда такие случаи действительно встречаются, но это не значит, что мы можем обобщить их для всех знаменитых памятников. Слишком легко переоценить важность случайных отношений, которые, к тому же, могут быть неверно измерены
********
Оказалось, что пересказывать таким образом статью с английского довольно утомительно, поэтому в этом посте примерно половина. Если людям будет интересно, выйдет вторая часть
Если интересны посты про науку и учёбу, заглядывайте ко мне в группу ВК и канал телеграм






Лига образования
6.6K постов22.8K подписчиков
Правила сообщества
Публиковать могут пользователи с любым рейтингом. Однако мы хотим, чтобы соблюдались следующие условия:
ДЛЯ АВТОРОВ:
Приветствуются:
-уважение к читателю и открытость
-желание учиться
Не рекомендуются:
-публикация недостоверной информации
ДЛЯ ЧИТАТЕЛЕЙ:
Приветствуются:
-конструктивные дискуссии на тему постов
Не рекомендуются:
-личные оскорбления и провокации
-неподкрепленные фактами утверждения
В этом сообществе мы все союзники - мы все хотим учиться! :)