Квантовые вычисления обретают новые возможности благодаря GKP-состояниям⁠⁠

Автор: Денис Аветисян

Исследование показывает, что приближенные GKP-состояния, несмотря на шум, могут стать ключевым ресурсом для универсальных квантовых вычислений в системах непрерывных переменных.

Работа демонстрирует, что фоковски-демпфированные GKP-состояния позволяют телепортировать как клиффордские, так и неклиффордские гейты, открывая путь к универсальной квантовой вычислительной платформе.

Идеальные состояния ГКП (GKP) требуют бесконечной энергии, что делает их нереализуемыми на практике, а возникающий шум обычно рассматривается как недостаток, требующий исправления. В работе 'Realistic GKP stabilizer states enable universal quantum computation' показано, что несовершенные, нормализуемые состояния ГКП, напротив, могут быть использованы в качестве ресурса для реализации неклиффордских гейтов с помощью исключительно линейно-оптических элементов. Ключевым результатом является возможность телепортации как клиффордских, так и неклиффордских гейтов посредством гауссовых операций и гомодинных измерений в рамках квантовых вычислений на основе измерений. Открывает ли это путь к созданию практичных и масштабируемых квантовых компьютеров на основе непрерывных переменных?

Понимание через устойчивость: Кодирование с помощью GKP-кодов

Квантовые вычисления, чувствительные к шумам, требуют надежных схем кодирования, превосходящих классическую коррекцию ошибок. Коды Готтсмана-Китаева-Прескилла (GKP) кодируют кубиты в непрерывные степени свободы, потенциально обеспечивая большую устойчивость к ошибкам, чем дискретные коды. Даже приближения GKP, такие как Фокк-затухающие состояния, позволяют осуществлять универсальные квантовые вычисления, демонстрируя устойчивость даже при несовершенстве исходных состояний.

Манипулирование квантовой информацией непрерывных переменных

Гауссовы операции служат универсальным набором инструментов для манипулирования квантовыми состояниями непрерывных переменных (CV), обеспечивая широкий спектр преобразований. Для универсальных квантовых вычислений необходимы не-гауссовы операции, но даже с использованием приближений, таких как затухающие состояния GKP, универсальность достижима. Приближенные состояния GKP снижают требования к точности экспериментальной реализации, открывая возможности для создания устойчивых и масштабируемых квантовых устройств.

Квантовые вычисления на основе измерений с CV-состояниями

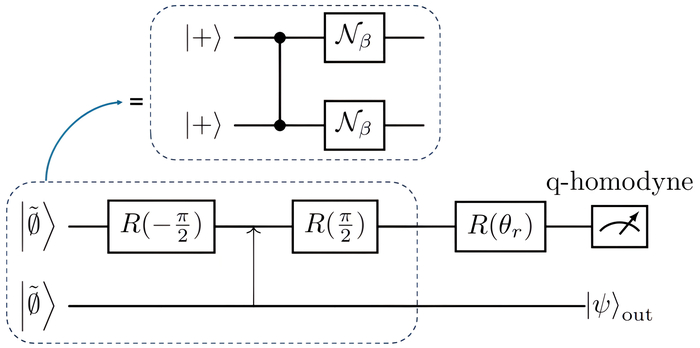
Квантовые вычисления на основе измерений (MBQC) – мощный подход к реализации квантовых алгоритмов, использующий запутанные ресурсные состояния. В качестве ресурсного состояния часто используются кластерные состояния. Необходимыми инструментами для реализации MBQC являются балансировочные лучеделители, фазовые сдвигатели и Q-гомодинное измерение, а математический аппарат функций Якоби играет ключевую роль в описании и манипулировании этими сложными состояниями.

Универсальность и роль магических состояний

Для достижения универсальных квантовых вычислений необходимы неклиффордовские гейты, требующие создания "магических состояний" – нестабилизированных квантовых состояний. Важным этапом является преобразование непрерывных квантовых переменных в дискретные кубиты. Интеграция кодов ГКП, MBQC и магических состояний представляет перспективный путь к отказоустойчивым универсальным квантовым вычислениям, демонстрируя реализацию как клиффордовских, так и непаулевских гейтов посредством телепортации с использованием рациональных параметров.

Исследование, представленное в данной работе, демонстрирует, что даже приближенные состояния ГКП, подверженные затуханию Фока, способны служить ценным ресурсом для универсальных квантовых вычислений. Этот подход позволяет телепортировать как клиффордовские, так и неклиффордовские гейты в системах непрерывных переменных. Данное открытие перекликается с мыслями Луи де Бройля: “Всякое явление можно рассматривать как распространение волны, а каждую волну — как скопление частиц.” Именно способность рассматривать приближенные состояния не как источник шума, а как проявление волновой природы квантовой информации, позволяет расширить границы возможностей квантовых вычислений и реализовать универсальные операции, опираясь на принципы, сформулированные пионером волновой механики.

Что дальше?

Представленные в данной работе результаты, безусловно, сдвигают парадигму восприятия состояний ГКП. Долгое время рассматриваемые как источник шума из-за неизбежных отклонений от идеальной формы, они теперь предстают ресурсом, необходимым для реализации универсальных квантовых вычислений в непрерывной области. Однако, следует признать, что истинное понимание требует дальнейшего исследования. Вопрос о влиянии различных видов затухания Фока, помимо рассмотренных, остаётся открытым. Необходимо тщательно изучить, как эти отклонения сказываются на точности телепортации неклиффордских гейтов, и какие методы коррекции позволят минимизировать возникающие ошибки.

Интересно, что дальнейшие исследования могут быть направлены на поиск оптимальных стратегий создания и поддержания состояний ГКП, учитывая реальные ограничения существующих квантовых устройств. Эффективное масштабирование системы, сохраняя при этом когерентность состояний, представляется сложной, но разрешимой задачей. Понимание пределов устойчивости состояний к различным типам декогеренции позволит разработать более надёжные архитектуры квантовых компьютеров.

В конечном счёте, данная работа заставляет задуматься о природе квантовых ресурсов. Вместо поиска идеальных состояний, возможно, стоит сосредоточиться на эффективном использовании тех, что доступны, даже если они не соответствуют теоретическим идеалам. Ведь именно в несовершенстве часто кроется ключ к новым возможностям.

Оригинал статьи: https://arxiv.org/pdf/2511.03874.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/