Используем рекурсию для решения задач на деревья. Ищем максимальную глубину дерева⁠⁠

В прошлой части мы рассмотрели разные подходы рекурсивного обхода дерева. Давайте воспользуемся некоторыми из них для решения довольно известных задач.

Находим максимальную глубину дерева.

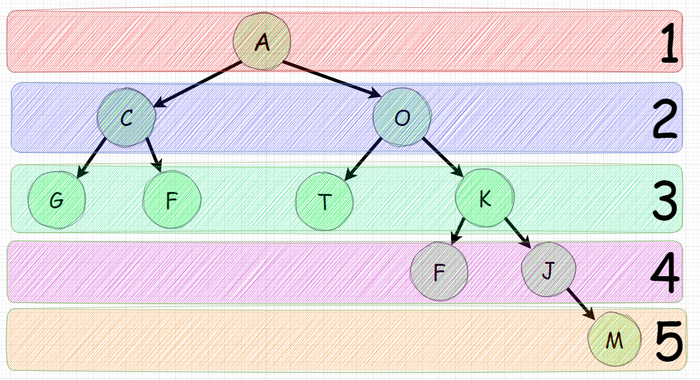
Одна из самых популярных и простых задач на деревья - поиск узла находящегося на максимально удаленом расстоянии. Рассмотрим дерево ниже:

Довольно очевидно что самый длинный узел в данном дереве - M и он является пятым по счету если головной является первым.

Как решать данную задачу используя рекурсию.

Если сильно упрощать то нам нужно сделать 2 действия:

• Обойти все узлы

• Каким то образом "сохранять" состояния каждый раз когда мы обходим узлы

Но как же сохранять состояния о той глубине на которой мы побывали? Тут есть как минимум два варианта:

• Использовать возвращемое значение самой рекурсивной функции и "возвращать" её на уровень выше.

• Иметь какой то объект в котором мы будем сохранять состояния находясь внутри рекурсии

Воспользуемся первым подходом. Сосредоточимся на следующих аспектах:

• Рекурсивная функция должна передавать значение сама себе "наверх"

• Определить какое именно значение должно перебрасываться.

Логика передаваемого "наверх" значения.

• Самые нижние уровни (те что указывают на null) должны возвращать 0 тк они не включены в расчет глубины данного подграфа

• Нижний уровень который с листьями имеет лишь null предков должен вернуть 1 тк он является первым уровнем

• Узел выше чем 1й (те не лист) должен выбирать максимальный уровень из двух его наследников и добавлять 1 тк находится на уровень выше из наибольшего из них.

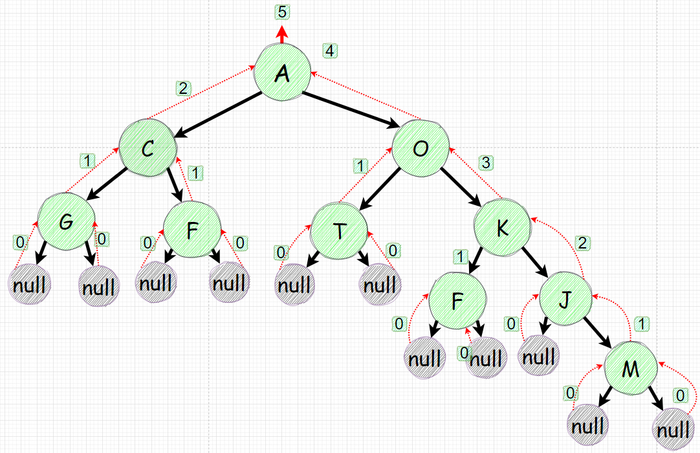
После данных рассуждений у нас вырисовывается вот такая картина:

К чему привели наши рассуждения?

Все эти рассуждения намекают что в нашей итеративной функциии будет 3 разных сценария и функция которая выбирает наибольшее из двух. Именно подобные размышления чаще всего помогают перевести абстрактные размышления в код.

И так первая версия кода:

Самый важная часть кода - итеративный вызов левого и правого поддерева и последующий расчет максимального значения среди них. И конечно же добавление 1 наибольшему из них чтобы учесть и текущую высоту.

Этот код можно было бы улучшить удалив случай когда мы находимся в самом низу - дело в том что если условие истино то возвращаемое значение maxDepth + 1 будет также равно 1.

Спасибо за внимание, всем кому интересна промышленная разработка приглашаю в мой канал.