[captain]
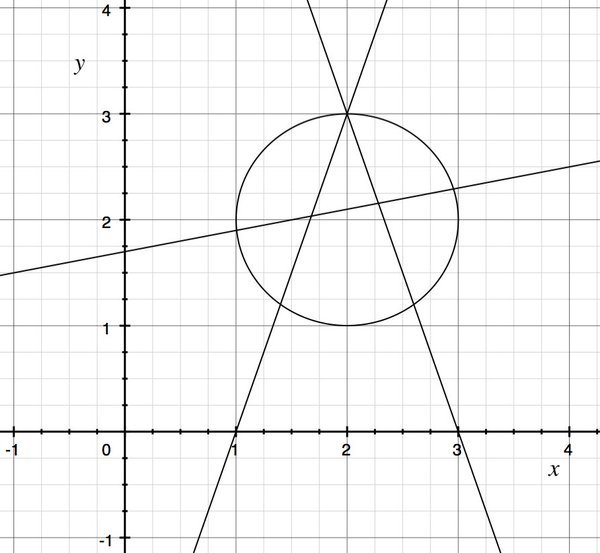
Во-первых можно составить функцию: «f(x,y) = (x-2)^2+(y-2)^2-1». Во-вторых, «функция» тут — это вообще лишняя сущность, достаточно просто писать уравнения вроде того же:
(x-2)^2+(y-2)^2-1 = 0
[/captain]
Не минусим человека - KasyanDiGris ниже все правильно пояснил #comment_63949147
Задавая функцию вида f(x,y) = (x-2)^2+(y-2)^2-1 мы получаем две независимых переменных, которые задают плоскость. В каждой точке этой плоскости функция принимает определенное значение, того получается трехмерный график.
А вам, XetaFelius, дам совет пояснять все поподробнее для гуманитариев
Как оппонент @KasyanDiGris добавлю:
Согласен. Не надо его(её?) минусить. Ответ у него(неё) аргументированный и вежливый, а значит можно вести конструктивный диалог.
Теперь по поводу вашей аргументации, самый лаконичный ответ написал(а) @samsonovislava вот тут #comment_63959031
Более развёрнутый и запутанный: #comment_63959316
ебать, неучи тебя заминусили. И в топе какая-то хурма от гуманитариев. Люди забыли, что уравнение окружности задается неявно, в качестве R^2=X^2+Y^2, где R - параметр, а не какая-та функция от 2 переменных, в результате чего переходим в так называемое 3д. Мне жаль за образование в нашей стране... Человек написал уравнение параболоида не к месту и думает, что умный...
Если человек гуманитарий, то у него в институте не было высшей математики, а значит он мыслит школьными терминами. А в школе приучивают думать, что значение функции — это варируемая переменная, которую необходимо использовать при построении графиков. В результате @XetaFelius считает, что задавая f(x,y) речь идёт про третью переменную.
Если что, то извиняюсь за свой сумбурный стиль речи :)
Простите, но:
Задавая функцию вида f(x,y) = (x-2)^2+(y-2)^2-1 мы получаем две независимых переменных, которые задают плоскость. В каждой точке этой плоскости функция принимает определенное значение, того получается трехмерный график.
Вы правы, если речь про график функции f(x,y), но я ничего не говорил про "график функции f(x,y)" :)
Более развёрнутый ответ: #comment_63959316
Геометрическое представление данной функции есть поверхность второго порядка, на что Вам указал @XetaFelius, и только с уточнением f(x,y)=0 имеет решение в виде окружности, чего Вы не сделали.
А без этого задаёт скалярное поле.
Из-за своего неумения корректно составлять уравнения, Вы назвали человека гуманитарием и перешли на оскорбления уровня "ты школьник".
Стыдно @socexp @SuzuShuto.
По математике: прошу перепрочитать мой самый первый комментарий в данной ветке (#comment_63940904 ), откуда и идут все эти споры.
Там есть "f(x,y) = (x-2)^2+(y-2)^2-1" и "(x-2)^2+(y-2)^2-1 = 0". Мне казалось, что вполне очевидно, что необязательно писать f(x,y) = 0, чтобы понять, как это можно получить самостоятельно.
Однако я это всё равно потом пояснил в других комментариях. Включая тот, на который сослался в комментарии, на который вы только что ответили.
По оскорблениям, прошу перепрочитать "по поводу шуток" в комментарии: #comment_63960498
Добавлю: Я никого школьником не называл. Мне просто как-то всегда казалось, что люди идут учиться по разным направлениям, и не у всех эти направления требуют изучения высшей математики. То есть вы читаете в моих комментариях то, чего я не подразумевал. Извиняюсь, если плохо сформулировал.
Это грубая ошибка, а не "очевидно". Эта функция и уравнение задают разные вещи.
Я говорю сугубо про комментарий #comment_63940904 ,с которого всё началось.
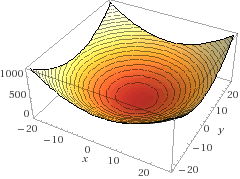
Функция вида f(x,y) = (x-2)^2+(y-2)^2-1 определяет поверхность второго порядка
(рисунок 1)
и является эллиптическим параболоидом с вершиной в точке (2;2;-1).
Ещё раз, но другими словами (надеюсь в последний):
Вы нарисовали график функции, но я ничего не говорил про график функции. Если дана функция, то не обязательно чертить по ней "график функции". Функцию можно использовать чтобы просто задать уравнение (в частности можно определить f(q,...) = 0). Например посмотрите на принцип наименьшего действия в классической механике (просто δS = 0) -- такая короткая запись, но такая ёмкая. И на основе её можно строить какие угодно графики для какой угодно задачи классической механики... меня немного в сторону понесло, возвращаемся к основное теме:
Линия, поверхность, тело, что-либо ещё можно описать уравнениями; а функця однозначно определяет лишь "график функции", о котором ни слова не было сказано в предыдущих комментариях. Эти графики используются обычно для изучения свойств функции, но не для выбора подмножества точек. Для выбора подмножества точек обычно используются уравнения.
То что нарисовали вы, это поверхность описываемая уравнением эллиптического параболоида:
(x-x0)^2/a^2 + (y-y0)^2/b^2 - c - z = 0
И действительно, z никто не запрещает записать в виде f(x,y) и перенести вправо, и в результате получить запись:
f(x,y) = (x-x0)^2/a^2 + (y-x0)^2/b^2 - c
А теперь то, из-за чего недоразумение: выше написано уравнение и об это явно сказано. Это уравнение описывает поверхность вроде той, что на вашем рисунке.
А я говорил про уравнение f(x,y) = 0, где функция f(x,y) = (x-x0)^2/a^2 + (y-x0)^2/b^2 - c, в результате, у вас уравнение:
(x-x0)^2/a^2 + (y-y0)^2/b^2 - c - z = 0
а я говорил про:
(x-x0)^2/a^2 + (y-x0)^2/b^2 - c = 0
Сразу напомню, что я явно сказал, что сущность "функция" -- тут вообще лишняя. Достаточно сразу говорить про уравнение вида:
(x-x0)^2/R^2 + (y-x0)^2/R^2 - 1 = 0
А что задаёт данная функция? Какое у неё геометрическое представление?
Несомненно лучше, но он этого не сделал.
Данный эллиптический параболоид - геометрическое отображение скалярного поля f(x,y) = (x-2)^2+(y-2)^2-1.
Заметьте, значения Z на оси нет.
Можно представить в таком виде.
если человек как-то раз получил пятерку по математике, он начинает шутить про "гуманитарием"
бтв, чтобы твоё уравнение/функция задавало двумерный график, оно должно представлять зависимость именно двумя переменными, независящую от других переменных.
f(x,y) = (x-2)^2+(y-2)^2-1 не задает двумерный график, а вот (x-2)^2+(y-2)^2-1 = 0 задает. хуевый из тебя капитан. гуманитарий наверное.
Тут ещё задолго до вашего комментария было и про f(x,y) = 0 #comment_63942199
Капитан из меня действительно хреновый, так как это мне казалось слишком очевидным чтобы писать в самом первом комментарии. Но как выяснилось действительно требовалось расписать всё намного подробнее, ибо в результате времени потратил намного больше.
А теперь по поводу вашей аргументации: #comment_63959316
По поводу "шуток". Я не шутил, а говорил вполне серьёзно. Более того, я не подразумевал никакого негативного смысла. Сам я по образованию инженер-физик -- это не делает из меня хорошего или плохого человека, а просто даёт мне понимание тех областей, которым меня учили. Смотря на аргументацию оппонента мне показалось очевидным, что такой высшей математики (как была у нас) у него и близко не было, иначе и диалога бы всего не было бы.
Я искренне прошу прощения, если я ошибся. Однако прошу сообщить об этом, чтобы я для себя мог сделать выводы. И сообщите, пожалуйста, сразу, где конкретно учились и на каком факультете.
вмк мгу 1-й курс:D
в той писанине вообще непонятно, что вы хотите доказать. это просто какой-то набор фактов, не преследующий какую-то цель) достаточно было сказать, что для определения нужного графика можно написать как
f(x,y) = (x-2)^2+(y-2)^2-1
f(x,y) = 0
так и
(x-2)^2+(y-2)^2-1 = 0
а не расписывать эпопею)
В самом первом комментарии ( #comment_63940904 ) и было про это. Разве что явно не было сказано, что "f(x,y)=0", так как переход казался слишком очевидным, чтобы его ещё и комментировать.
По поводу эпопеи, расписана она потому, что некоторым комментаторам тут не хватило простого f(x,y) = (x-2)^2+(y-2)^2-1 и f(x,y) = 0 для понимания происходящего.
Однако, без этой писанины ты нихера не понял, а ведь человек в своем первом комментарии именно это и написал. Хотя от вмкашника первокурсника требовать ничего нельзя
Никто никогда так не приучает думать
Наоборот стараются как можно сильнее отделить понятия значения функции и аргумента(варируемой переменной)
Спешу посеять хаос в твою теорию. Такую запись "f(x,y)" проходят в 8-9 классе. Человек не то что высшую математику не изучал, а просто подзабыл школьную, наверное
Функции нескольких переменных изучают на матанализе первого курса. И в целом ничего страшно сложного в них нет, чтобы не запомнить хоть что-то из этой темы
Ты не поверишь, но
у=х - функция от двух переменных (так как оси на графике 2)
функция вида x^2+y^2=R^2 - та же функция от двух переменных, просто задана неявно
а вот z=x^2+y^2 - функция от трех переменных, а именно параболоид, вот параболоид это 3д
кто плюсует этот бред? y=x ф-я одной переменной. x^2+y^2=R^2 это вообще не функция а уравнение окружности. просто в любой точке этой окр-ти за исключением (-r,0),(r,0) если взять достаточно малую окрестность то в ней уравнение можно представить как ф-ю y=f(x)(ф-я одной переменной)
еще один псевдоумник.
x^2+y^2=R^2 - это называется неявно заданная функция. с остальным согласен.
это называется уравнение окружности. если ты возьмёшь дугу не содержащую точек(r,0),(-r,0) то ты получишь подмножество R^2 которое с любой прямой вида x=const имеет не более одной точки пересечения. это подмножество удовлетворяет определению функции. ЭТА ФУНКЦИЯ И ЕСТЬ НЕЯВНО ЗАДАННАЯ ФУНКЦИЯ.
А про неявную функцию что-то слышали?) ну так вот окружность - это неявная функция)
А судя по тому что вы ничего не сказали про парабалоид вы даже не знаете что это хд
Не факт. Их может быть сколько угодно.
Например, функция y(x) = 5 задаёт прямую в 2-мерном пространстве,
y(x1, x2) = 5 — в 3-мерном и так далее.
Так же и функция y = x, может быть отображением не R -> R, а Rn -> R, правда от всех переменных, кроме первой, значение функции не будет зависеть :)
Формально, это вещественная функция, т.к. она задаёт отображение
Rn -> R однозначным образом.
x=5 может обозначать точку на оси ox, прямую параллельную оу проход через точку (5,0), плоскость проходящую через точку(5,0,0) и тд. и это НЕ функция а уравнение! Окружность это кривая её дуги за исключением дуг содержащих точки(r,0) или(-r,0) можно представить как функции y=f(x)(это и есть неявная функция). и вообще ты не не понимаешь что такое функция. Зорича или Фихтенгольца почитай и не позорься больше.
Я и не сдвигался. Очень грубо говоря (некорректным, но понятным языком):
Нужные точки задаются уравнениями, а не функциями. Функция — это лишь соответствие между элементами множеств. А уравнения — это ограничители, которые можно, в частности, использовать чтобы из полного множества точек выбрать лишь нужные. [Как можете догадаться, система уравнений — это когда задаётся одновременно несколько «ограничителей», что тоже можно использовать для такого рода рисования].
Так вот, можно задать функцию f(x,y), а потом задать уравнение: f(x,y)=0. Таким образом можно в «2D» (выражаясь в ваших терминах) определить желаемый набор точек.
Я могу IRL разжевать всё намного подробнее, если интересно, и если вы в Москве. ;)
себе разжуй. ты применил в своём коменте функцию от двух аргументов, "умник". Это лишняя сущность. и это не тоже самое, что уравнение.
Херовый из тебя капитан короче.
Дык я и говорю, что у него функция от двух переменных. Это не уравнение, которое задаёт нужную нам вещь.
Это вы умничащие дебилы, на первом курсе застряли и внимательности не научились. Говнобушники.
Например я считаю, что за конструктивный диалог минусовать глупо. Но, к сожалению, "чувак" не желал вести диалог конструктивно. Пирамида Грэма неплохо описывает ценность комментариев, IMHO.
Я знаю, что это лишняя сущность, я об этом и сказал тут:
А то, что это не то же самое, что и уравнение, я написал и там и даже в комментарии, на который вы написали свой возмущение :)
Меня тоже добавил :D
Видимо это защитная реакция гуманитария на попытку объяснить ему матанализ хд
да ппц тут веточка, прицепились друг к другу из-за неточностей в описании, хотя даже гуманитарию понятно, что они просто доебываются друг до друга
Он художник - он так видит.
Вы еще к Пушкину придеритесь, мол что такие длинные обороты использует.