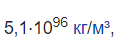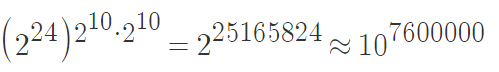Не знаю, как у вас, но я в детстве с друзьями иногда играл в своеобразную "игру" — у кого больше. Начиналось все примерно с миллиона, а заканчивалось конструкциями типа "А у меня бесконечность бесконечностей бесконечностей бесконечностей и так бесконечность бесконечностей раз!".
Математики тоже играют в такую игру, но у них числа больше и невообразимее, чем могут придумать себе младшие школьники, а изложение строже и точнее.
Этот пост навеян вики-сообществом "Гугология" и несколькими популярными изложениями: тык, тык, тык. И я бы не писал этот пост, если бы то, что рассказывают о больших числах, было изложено понятно, на русском и без неточностей. А еще мне нравится выпендриваться)))
Для понимания темы нужно знание математики до 7-8 класса, воображение и немного абстрактного мышления.
Начнем с какого-нибудь не особенно большого числа, например, триллион. Записывается триллион как 1 000 000 000 000 или короче — как 10 в 12 степени. Это число не особенно большое в сравнении с теми монстрами, о которых еще поговорим — более того, его можно очень легко представить.
Возьмем шарик от шариковой ручки — его размер примерно равен одному миллиметру, а объем — одному кубическому миллиметру. Один кубический метр равен миллиарду кубических миллиметров, а объем олимпийского бассейна — примерно 2000 кубических метров. Перемножаем и получаем, что целых 2 триллиона шариков от шариковых ручек может поместиться в одном олимпийском бассейне. И если вы можете представить объем олимпийского бассейна и объем шарика одновременно — поздравляю, вы представили триллион! Даже два!
(Картинки из гугла, чтобы помочь воображению™)
Этот трюк плохо работает с триллионом, расположенным в одну линию, например, триллион секунд составляет около 30 000 лет, что для многих неожиданно много.
А таким "объемным" способом можно представить себе числа вплоть до масштабов квинтиллиона — или 1 000 000 000 000 000 000, или 10 в 18 степени.
Нередко в физике встречаются числа и больше, например, масса Солнца в килограммах (10 в 30 степени) или энергия сверхновой звезды в джоулях (10 в 46 степени). (В одной калории примерно 4 джоуля).
Далее по списку идет знаменитый гугол — 10 в 100 степени — число уже достаточно большое, чтобы даже в физике почти не нашлось ничего похожего. Пожалуй, ближе всего к гуголу в мире физики подобралась т.н. "планковская плотность", или
что всего лишь в 2 тысячи раз меньше гугола. Ну а самое большое число, имеющее хоть какой-то физический смысл прямо сейчас — это 10 в 185 степени, или количество планковских объемов — самых маленьких частей пространства в физике — в наблюдаемой части вселенной.
Есть числа и гораздо большие, которые имеют смысл в комбинаторике — области математики, которая, грубо говоря, изучает количества сочетаний разных элементов.
Например, количество всех возможных картинок размером 1024x1024 пикселя можно представить как количество всех возможных таблиц пикселей размером 1024x1024. Каждый пиксель может быть раскрашен в один из 16,8 миллиона цветов, а всего таких пикселей примерно миллион. Теперь, если грамотно все подсчитать, получится число
то есть 10 в 7 600 000 степени.
Представить такое число напрямую уже нельзя, но косвенно можно — дело в том, что все возможные картинки размером 1024x1024 пикселя содержат:
Все возможные фото всех людей, существовавших или не существовавших на земле во всех мыслимых и немыслимых позах, во всех мыслимых и немыслимых местах.
Все картины, когда либо написанные и еще не написанные, во всех возможных стилях.
Все картины и фото из предыдущих двух пунктов, но у которых на верхний левый угол наложено кофейное пятно фильтром из фотошопа.
Все картины и фото из двух первых пунктов, но к каждой из них различным образом прифотошоплен свидетель из Фрязино.
Все сканы страниц всех книг, которые написаны и не написаны, в том числе те, что отсканированы плохо.
Может быть, где-то в этом множестве есть та самая картинка из крипипасты, вызывающая у людей ужас и заставляющая вырывать себе глаза.
Но при этом подавляющая часть этих картинок выглядит примерно так:
Так вот, всего таких изображений как раз 10 в 7 600 000 степени.
Кстати, очень похожая концепция описана в рассказе Хорхе Луиса Борхеса "Вавилонская библиотека", рекомендую.
В следующем посте погрузимся немного в математику и достанем до числа Грэма. Дальше посмотрим на быстрорастущую иерархию функций. Потом расскажу про т.н. "невычислимые функции", и в конце, может быть, рассмотрю уже иерархию бесконечностей.
Правда, если просмотров и комментариев будет мало, то продолжать не стану, наверное.
Адекватные претензии по форме и содержанию приветствую.
P.S. Второй пост