Ответ на пост «Парадоксы скорости света. Часть 5»
И так, объясняю все эти парадоксы разом. Парадоксы это классический цирковой фокус, в котором фокусник отвлекает ваше внимание на задницу ассистентки, пока достает кролика из под куртки и сажает его в шляпу. Следите за руками внимательно:
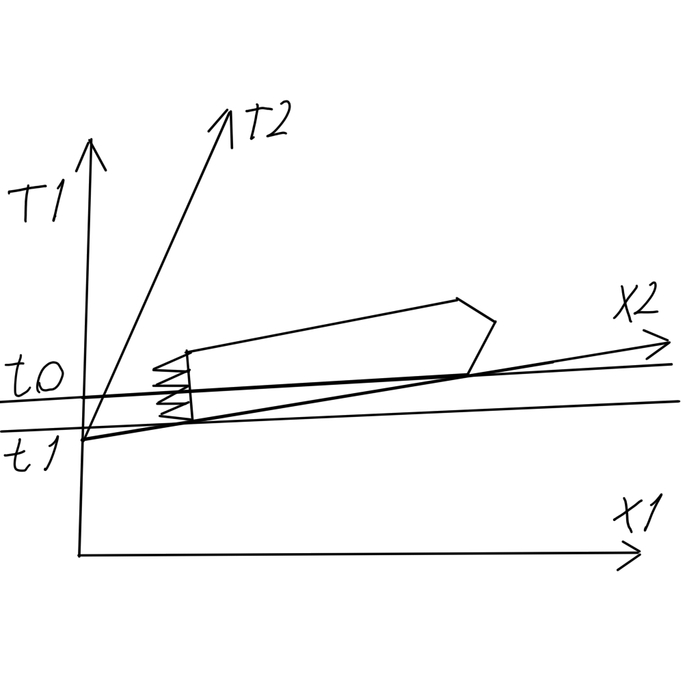
Берем лист бумаги и рисуем на нем ось времени T1 и ось пространства X1. Это система отсчета неподвижного наблюдателя. Теперь рисуем систему отсчета движущейся ракеты. Ось времени T2 и ось пространства X2.
Классическая механика: ось T2 будет повторять траекторию движения ракеты. Потому что наблюдатель летит по этой траектории и говорит "время движется, а я - нет. Я неподвижен". Ось X2 будет параллельна X1.
СТО: фокусник говорит "E=MC^2! Крибле-крабле-бумс!" и вы отвлекаетесь на эти слова. В это время этот хитрец незаметно берет ось X2 и поворачивает ее относительно оси X1. Чем быстрее летит ракета, тем больше поворачивает. Зрители слишком заняты странными заклинаниями и не видят этого. Но именно в этом состоит главный секрет всех фокусов СТО. А наша картинка называется "Диаграмма Минковского".
Что происходит, когда ось X2 поворачивается? Корма ракеты проваливается в прошлое, а нос - в будущее. То есть, если, допустим, с точки зрения движущегося наблюдателя на корме и носу одновременно зажгут огни, то с точки зрения наблюдателя неподвижного сначала загорится огонь на корме в момент t0 (она в прошлом) и только потом на носу в момент t1 (он в будущем). Относительность одновременности.
Что происходит в парадоксе близнецов?
* Два близнеца стоят в космопорте. Один из них меняет свою скорость улетев на ракете. Но как скорость не меняй, они в одной точке пространства-времени. Не происходит ничего, кроме того, что время близнецов замедляется друг относительно друга. Да, они оба видят что время брата стало идти медленнее.
* Близнец долетает куда ему было надо и разворачивается. В этот момент он меняет свою скорость и его ось X снова поворачивается. И тут происходит фокус - в новой системе отсчета космонавта, время неподвижного брата (точка пересечения с повернувшейся осью X) изменилось. Наш космонавт этого не видит, потому что фотоны от постаревшего брата еще не дошли. Но геометрически выходит вот так - бац! и брат постарел. А если развернуть ракету в обратную сторону, то бац! и обратно омолодился. Вот это весь парадокс и съедает.
Что происходит, когда две ракеты летят друг другу навстречу? Их оси X идут не параллельно, а пересекаются крест на крест. Вот именно поэтому оба наблюдателя на ракетах и видят что другая ракета не превышает скорости света.
Все прочие магические формулы просто подогнаны так, чтобы гарантировать постоянство скорости света. Именно подогнаны. Постоянство скорости света не следует из формул, это формулы следуют из постоянства скорости света. Но главный фокус-покус здесь именно в повороте оси X.