Вся Россия. 2021
Данные по 96840 участкам (107,9 миллиона зарегистрированных избирателей из 109.2 по ЦИК).
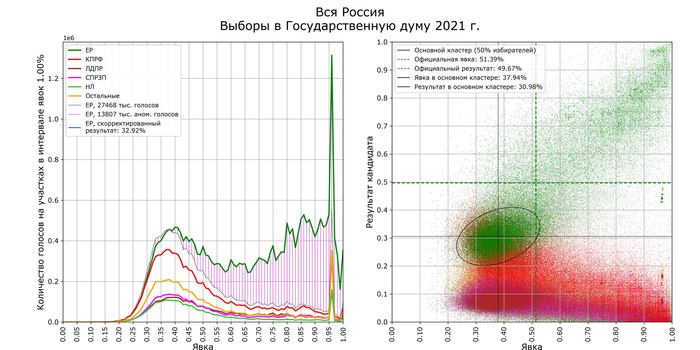
Слева - гистограмма голосов за партии по 1% интервалам явки, тонкая линия - гистограмма голосов за все партии кроме ЕР, масштабированная так, чтобы совпасть с гистограммой за ЕР на начальном участке. В предположении (строго говоря неверном), что все фальсификации за ЕР - чистый вброс, заштрихованная площадь дает размер вброса - 13,8 млн голосов, что составляет половину всех голосов за ЕР.
Справа - результаты партий в зависимости от явки по участкам, каждый участок - набор точек разных цветов для соответствующих партий. Плотное ядро - предположительно нефальсифицированные участки, центр ядра для ЕР определен методом Minimum Covariance Determinant с взвешиванием участков по количеству избирателей и порогом отсечения 50% (проще говоря - строится эллипс минимальной площади, содержащий половину всех голосов - прим. ТС). Соответственно координаты центра ядра для ЕР дают оценку реальной явки и реального результата ЕР.
На нефальсифицированных участках явка в среднем 38% (как в 2016 году), ЕР получает по двум оценкам от 31% до 33% (как в 2011 году).
Что отдельно примечательно - уменьшились (но остаются далеко выше порога значимости, как посчитал Д. Кобак) пики в распределении голосов на целочисленных процентах.
"Зуб" на явке 95% - это московское электронное голосование.


Статистика
941 пост3K подписчиков
Правила сообщества
1. Не нарушать правил pikabu
2. Постить контент относящийся к теме сообщества