Верите ли вы в случайность?⁠⁠

Я задался этим вопросом, когда внезапно мне пришел подарочный набор игральных костей для игры в D&D (спасибо @Zarkon!). Для тех, кто не в курсе, если таковые есть - большая часть игровых механик завязана на использовании кубиков с 4, 6, 8, 10, 12 и 20 гранями. Есть ещё бросок к100, но он достигается броском двух кубиков к10. В идеале каждый такой бросок - рандом, абсолютная случайность, которая и определяет успешность тех или иных действий. Но так ли это на практике?

В моем наборе каждая кость представляет собой полупрозрачный материал, и в каждой из костей залито Кольцо Всевластья. Из-за этого, предположил я, центр масс костей может быть смещен, если масса колец отличается от остальной массы кости. Как будем выяснять?

Интернет предложил мне сразу два метода. Один - самый простой. Готовится очень насыщенный раствор соли в стакане - в теплую воду добавляем несколько ложек соли до тех пора, пока она не перестанет растворяться. Достаточно около 20 градусов - в таком случае на 100 грамм воды придется около 36 граммов поваренной соли. Для сравнения - при 100 градусах та же масса воды растворит 39 грамм.

Задача простая - кинуть в стакан кость и посмотреть, какой гранью она будет всплывать. Если после нескольких опытов она всплывает одной стороной или тремя смежными к ней - то кость явно не сбалансирована и будет чаще падать именно этими сторонами вверх. Тут вроде понятно. Пробуем:

Ага. Как оказалось, этот метод подходит не для всех костей - а только для пластиковых, чей удельный вес ниже соляного раствора. В моем случае кости из эпоксидной смолы, так что бессмысленно пытаться выяснить это таким образом. Ну что ж, тогда обратимся к силе математики!

Если вы подбросите монетку, что она упадет орлом или решкой с вероятностью 50%. Это в принципе понимают все. Если вы подбросите ее три раза, то с вероятностью в 12,5% у вас выпадет три одинаковых значения. Также существует вероятность, что при 10 бросках 7 из них - будут либо орлом, либо решкой. Значит ли это, что вероятность выпадения того или иного значения выше? Конечно, нет!

В теории вероятностей есть принцип, который называется "Закон больших чисел". Он гласит, что при достаточно большом количестве выпадения случайных чисел их соотношение будет стремиться к математическому ожиданию. То есть, если вы подбросите монетку не 10 раз, а скажем, 2000, то количество орлов и решек будет стремиться к тем самым 50%.

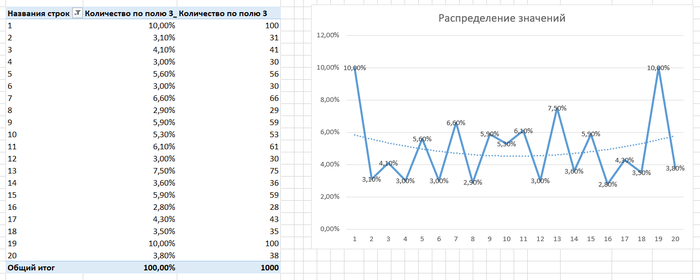
Соответственно, если мои кости сбалансированы, и я возьму, скажем, кость к20, то при большом количестве бросков каждое значение должно выпадать в 1/20 случаях, или 5%. Что ж, к коллайдеру! Задача простая - бросить кубик, скажем, 1000 раз, записать каждый результат и затем построить график распределения результатов. Сказано - сделано:

Что мы тут видим? На тысячу результатов у нас два значения, далеко выбивающиеся от остальных - 1 и 19, которые имеют 10% шанс выпадения, или 100 результатов из 1000. Остальные значения выпадают с большей или меньше долей вероятности, но остаются примерно равны по возрастанию, так что линейная линия тренда будет прямой и будет в районе ровно 5%. Из этого можно сделать вывод, что сам по себе дайс не позволяет получить преимущество или наоборот, так что нечестного преимущества кость не даст - она лишь даст вдвое больше шанса критического провала или практически успешной проверки (что весьма неплохой повод рискнуть), но при этом в среднем шансы высокого или низкого результата примерно равны.

Но самое интересное другое. Видно, что все положительные пики - нечетные (кроме 3 и 10). И хоть распределение их относительно равномерно, мы можем убедиться, что в 70 процентов случаев выпадают нечетные числа. Связано это с тем, как значения распределены на кости. 1 и 20 являются своеобразными вершинами полушарий, вокруг которых находятся соответственно нечетные и четные значения. И судя по тому, что я вижу, кость действительно несбалансирована, а линия тренда сохраняется лишь за счет распределения значений на ней. Итог - кость не сбалансирована, и нечестное преимущество за ее счет не получить, а вероятность выпадения критической единицы примерно втрое выше, чем критического успеха.

Что характерно, это же показывает и полиноминальная линия тренда на графике, которая показывает более высокие шансы выпадения крайних значений и менее высокие - средних. В целом - такой результат меня устраивает, потому что как мастер, я заинтересован в том, чтобы сражения моих игроков были более интересными и сложными за счет более высокого шанса попасть по ним, а с другой - дать им больше азарта в случаях, когда их враги будут промахиваться в критические моменты. Как игрок, я готов рискнуть более высоким шансом на провал, если при этом у меня будет больше возможностей пройти сложную проверку или попасть по противнику.

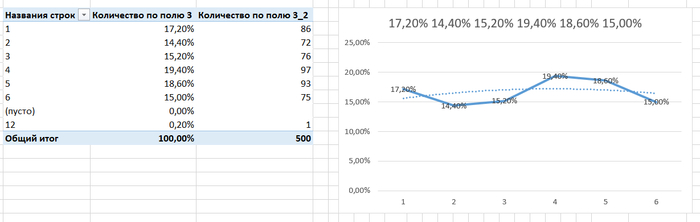
На этом я не остановился и решил проверить то же самое для кости к6. Я решил, что будет достаточно 500 бросков. И вот что я получил:

Здесь даже полиноминальная линия тренда достаточно гладкая, и это показывает, что кость хоть и несбалансированная, но куда ближе к среднему значению в 16,67%. В целом, я бы сказал, что это хороший показатель, особенно в свете того, что идеально сбалансированные кости встречаются очень редко - даже гравировки на гранях вносят свои корректировки и могут незначительно повлиять на распределение.

Кстати, вы можете попытаться создать последовательность случайных чисел аналоговым методом. Например, даже если кость идеально сбалансирована, опытные шулеры умеют бросать кости так, чтобы с большей вероятностью получать нужные значения. Да есть целая статья на Вики на эту тему (нет, так вы не научитесь и мастером-шулером не станете).

Да и вы сами - как показывает практика, попытка представить себе случайную последовательность неизменно сталкивается с когнитивными искажениями.

А вот так. Доказано, что человек, пытаясь представить себе случайную последовательность чисел, например, будет избегать повторений одного и того же числа, потому что это несколько отличается от наших внутренних представлений о рандоме. А между тем при бросках кости я пять раз сталкивался с ситуацией, когда у меня 4 раза подряд выпадало одно и то же значение.

Но это ладно. Многие играют по сети и кидают кубики онлайн. Может хоть там честные случайные числа? А вот не совсем. Каждый, у кого есть базовое понимание, как работают компьютеры, понимают, что это сугубо логические алгоритмы. Нельзя задать им задачу просто "выбрать случайное число". Они попросту этого не умеют (к слову, это и в случае людей справедливо). Поэтому в ход идут разного рода ужимки.

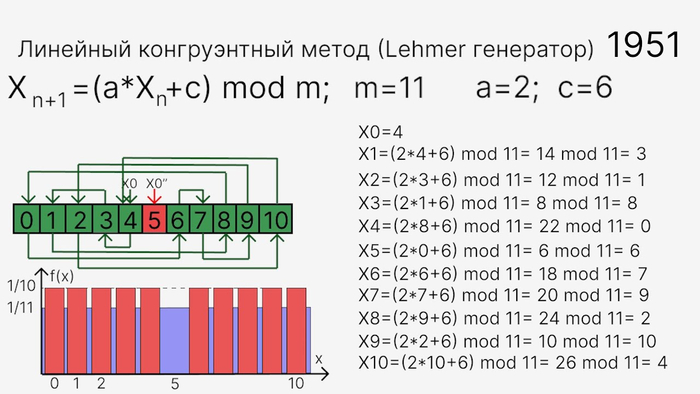
Самый простой вариант - берется какое-либо базовое число, чаще всего переменная, она обвешивается разного рода алгоритмами и вычислениями, и на выходе мы получаем какое-то число. Оно называется псевдослучайным, потому что как вы понимаете, если мы знаем алгоритм и значение переменной, то не составит труда пересчитать его и получить якобы случайное число. В качестве семени, т.е. начальной точки чаще всего используется время как отправная точка, с которой начинается генерация. И при внешней случайности числа под капотом точный алгоритм. Такой метод получил название линейного конгруэнтного метода.

Разумеется, этот метод предсказуем, и потому ученые разработали множество своих вариантов алгоритма типа метода Фибоначчи или Вихря Мерсенна. Некоторые доходили до паранойи в попытках создать фактически не просчитываемый алгоритм и можно сказать, что почти преуспели. Кроме того факта, что это все ещё логические вычисления, они стали настолько сложны, что их расшифровка в конечном счете превращается в крайне неблагодарное занятие:

Однако я вас все таки обрадую. Наиболее приближенные к настоящим случайным числам есть Просто в качестве "семени" в таких алгоритмах выступают не просчитываемые значения или переменные типа времени, которые можно посчитать. В таких алгоритмах в качестве источника используются значения, которые фактически не отслеживаются - шумы токов, такты процессора, размеры жесткого диска, номера процессов, тепловые шумы и даже радиоактивный распад элементов.

В таком случае шансов предугадать последовательность псевдослучайных чисел фактически нет. Это очень дорогие, медленные и затратные методы, они часто используются в криптографии и считаются наиболее надежными на текущий момент.

Так что, если задуматься, все случайные значения и события, черные и белые полосы в жизни - есть ни что иное, как сочетание факторов от смещенного центра тяжести костей до когнитивных искажений и хитрый математических последовательностей. Считать это случайностью или нет? Это каждый пусть сам для себя решит.

А на сегодня всё! Следующий пост уже совсем скоро. Подписывайтесь, чтобы не потеряться, а в перерывах между постами можете найти меня здесь:
https://t.me/MorBook
https://vk.com/badabook

Огромнейшее спасибо всем, кто читает, плюсует и комментирует мои посты. особенное спасибо тем, кто поддерживает выход новых постов донатом: @forgerm, @RamilM1979, @Bezeus, @Cheshire93 и ещё одному таинственному пикабушнику. Оригато!