Ответ TheSecondI в «Считаете арифметику скучной?»3
Вопрос вписывания прямоугольника в прямоугольник "впритык" (решение вопроса-поста)
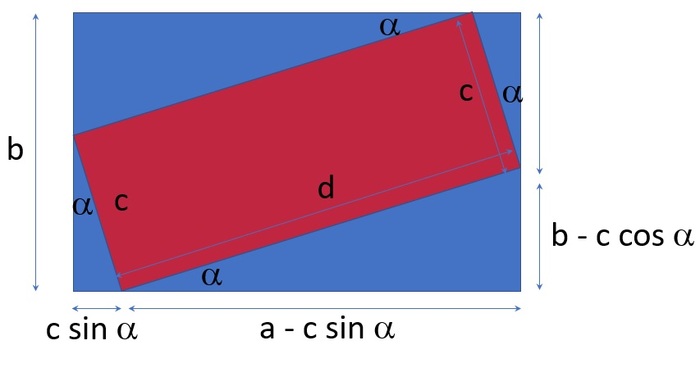
Пусть a — ширина основного прямоугольника, b — длина основного прямоугольника, c — ширина вписываемого прямоугольника и d — длина вписываемого прямоугольника (неизвестно), α — угол наклона (неизвестно).
Вписываемый прямоугольник лежит на сторонах основного прямоугольника.
Частная задача (в посте-вопросе): максимум длины вписываемого прямоугольника (по размерам основного и ширине вписанного прямоугольника).
Общая задача: найти по имеющимся нескольким значениям другие значения.
ОБЩЕЕ РЕШЕНИЕ
1. Как найти длину вписанного прямоугольника по формуле, при a=4; b=3; c=1 (в один клик):
Ответ: d≈4.0851, α≈31.7501
Инструмент ищет угол наклона/любую сторону, если есть 3 из 5 показателей
(вставьте свои значения вместо a, b, c, d, α)!
2. Подробное описание решения (методом Крамера и матрицами):
3. Решение, предложенное @vardader (#comment_364405448), кстати, верное (обратные знаки, на нахождение корней не влияет). При a=4; b=3; c=1:
Выходит четыре ответа, из них только одно действительное, а остальные отрицательные и комплексные: d≈4.0851, α≈31.7501
Справочно:
4. До угла в градусах
α = arctan((a*c-b*d)/(b*c-a*d))*180/π
дошли так.
1) Известно (система уравнений):
d*сos(α)+c*sin(α)=a
c*cos(α)+d*sin(α)=b
2) Перемножаем крест накрест:
b*(d*сos(α)+c*sin(α)) = a*(c*cos(α)+d*sin(α))
3) Раз мы знаем, что tg(α) = sin(α)/cos(α), то делим обе части уравнения на cos(α):
b*d+b*c*tg(α) = a*c+a*d*tg(α)
4) Переносим часть с тангенсом в одну сторону, выносим его за скобки, выражаем его отдельно:
b*c*tg(α) - a*d*tg(α) = a*c - b*d
tg(α) (b*c - a*d) = a*c - b*d
tg(α) = (a*c - b*d) / (b*c - a*d)
5) Из численного значения tg(α) получить
- радианы можно через арктангенс, или единица делить на тангенс: 1/tg(α)=arctan(α),
- градусы можно при домножении ещё на 180/π: arctan(α)*180/π
Таким образом, угол наклона в градусах:
α = arctan((a*c-b*d)/(b*c-a*d))*180/π
Справочно:
5. Ещё смежные вопросы рассматривались здесь
#comment_364391099
Теперь с помощью этого инструмента Wolfram Alplha, имея три стороны двух прямоугольников, можно находить четвёртую недостающую и угол наклона!
В том числе, имея a, b, c, можно находить длину d вписываемого прямоугольника, в чём и был вопрос.
Проблема решена

Лига образования
6.5K постов22.8K подписчиков
Правила сообщества
Публиковать могут пользователи с любым рейтингом. Однако мы хотим, чтобы соблюдались следующие условия:
ДЛЯ АВТОРОВ:
Приветствуются:
-уважение к читателю и открытость
-желание учиться
Не рекомендуются:
-публикация недостоверной информации
ДЛЯ ЧИТАТЕЛЕЙ:
Приветствуются:
-конструктивные дискуссии на тему постов
Не рекомендуются:
-личные оскорбления и провокации
-неподкрепленные фактами утверждения
В этом сообществе мы все союзники - мы все хотим учиться! :)