Ну вообще это есть такие задачи: нужно заменить каждую букву на какую-то цифру, чтобы получилось верное выражение. При этом разным буквам не могут соответствовать одинаковые цифры, а одинаковым буквам должны соответствовать одинаковые цифры. Только вот эту конкретную задачу у меня чет не получилось решить: либо недоглядел, либо она нерешаема.
Ну а "meow+meow=cat" из заголовка точно нерешаема в группе обычных целых чисел с обычным сложением, так как в сумме не может быть меньше цифр, чем в слагаемых. В какой-нибудь группе вычетов, может, решаема, но так неинтересно.
(долбанная профдеформация, ревьюю код для ребуса)
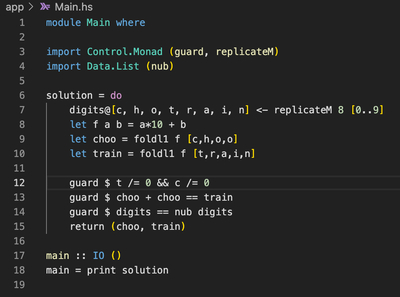
да лучше например permutations использовать, быстрее гораздо если порождать только варианты где все цифры изначально разные
train - чётное от 10234 до 19876
сhoo - от 5122 до 9877(что снижает максимальный train до 19754)
дальше можно брать все чётные train, делить на 2 и смотреть, соответствует результат шаблону или нет
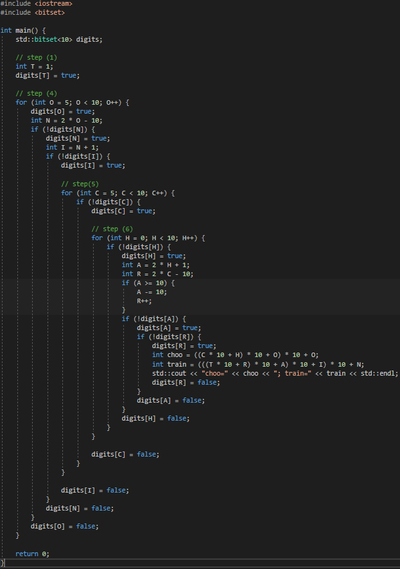
1. T=1, т.к. имеет место перенос из младшего разряда. Для этого необходимо C>=5.
2. Для того, чтобы суммирование OO+OO давало две разных цифры IN, также необходимо O>=5. Кроме того, справедливо I=N+1. Элементарно доказываем, что N - четное.
3. Исходя из п.2 знаем, что имеет место перенос в разряд A, т.е. A=2*H+1 (mod 10).
4. Зафиксировав O>=5 однозначно определяем I и N.
5. Пытаемся выбрать C>=5 отличное от {O, I, N}. Если это невозможно - возвращаемся к шагу 4 с другим O. Выбор C определяет R с точностью до переноса от 2*H+1, необходимость которого пока неизвестна.
6. Перебираем H по всем цифрам кроме {T, O, I, N, C}. Если 2*H+1<10 - переноса в следующий разряд не будет, R=2*C; иначе R=2*C+1. Т.е. первым делом смотрим, какое получается R, и если такая цифра уже есть в множестве {T, O, I, N, C, H} - проверяем следующее H; если все возможные H проверены - возвращаемся на шаг 5 с другим C. Далее вычисляем A=2*H+1 (mod 10) и аналогично смотрим, есть ли такая цифра в множестве {T, O, I, N, C, H, R}; если есть - переходим к следующему H; если все возможные H проверены - переходим на шаг 5 с другим C. Если A не входит в множество {T, O, I, N, C, H, R} - нашли одно из решений.
Шаг 4 - перебор по O из 5 вариантов. Шаг 5 - перебор по C не более чем из 4 вариантов (т.к. условия O>=5 и C>=5 пересекаются). Шаг 6 - перебор по H не более чем из 5 вариантов. Т.е. все решения можно найти перебором с возвратом не более чем за 5*4*5=100 шагов. Это реально сделать на листочке, используя ластик и простой карандаш.
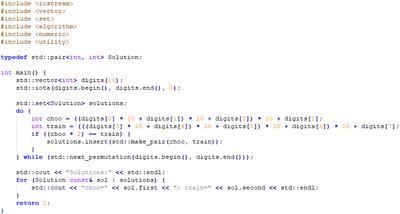
Перебор для каждой из 8 необходимых цифр от 0 до 9 требует 10^8 шагов. Генерация всех перестановок 10 цифр и проверка первых 8 из них на выполнение условия (как в написанной мною выше программе) требует порядка 3.6*10^6 шагов. Генерация всех сочетаний по 8 цифр из 10, и проверка условия для всех возможных перестановок для каждого сочетания требует порядка 1.8*10^6 шагов.
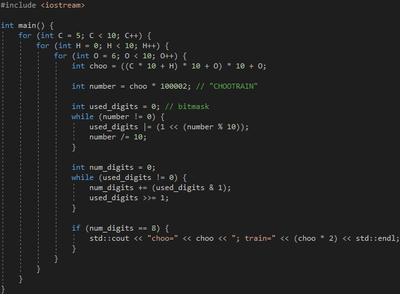
Нужно добиться того, чтобы в записи числа CHOO*100002 было использовано 8 разных цифр. Возможно, есть красивое решение без перебора вовсе.
Короче, нужно ковырять вот такое число (CHOTRAIN):
10002000 * C + 1000200 * H + 100022 * O.
Очевидно, для каждого из чисел { C, H, O } нужно рассматривать два варианта, меньше 5 и больше 5 (получается перенос в 1-4 разрядах). Из соображений пп.1-2 тремя постами выше варианты C<5, O<5 отбрасываем. Остается два варианта для H, для них нужно аккуратно всё расписать:
первая цифра: 2*O-10;
вторая цифра: 2*O-9;
третья цифра: 2*H+1 (при H<5) или 2*H-9 (при H>=5);
четвертая цифра: 2*C-10 (при H<5) или 2*C-9 (при H>=5).
пятая цифра: 1;
шестая цифра: O;
седьмая цифра: H;
восьмая цифра: C.
Рассматриваем два случая по H и пытаемся подобрать { C>=5, O>=6, H } чтобы все восемь цифр были различны.
Добил задачку.
Рисуем по три таблички для случаев H<5, H>=5. В каждой табличке вычеркиваем строки с повторяющимися цифрами, во второй и третьей табличке вычеркиваем строки с единицами (т.к. T=1).
Теперь нужно найти сочетания из строк трех таблиц, в которых нет повторяющихся цифр. Полный перебор - 72 варианта, но можно быстрее.
Сначала находим подходящие строки второй таблицы к каждой строке первой таблицы. Для каждого найденного варианта далее ищем подходящие строки из третьей таблицы. Итого, нужно проверить всего 42 варианта.
Если допустить, c или t могут быть равны нулю, то получаем ещё 6 решений:
choo=1488; train=2976
choo=2188; train=4376
choo=4566; train=9132
choo=4588; train=9176
choo=4766; train=9532
choo=4866; train=9732
Кар+кар=ворона
ква+ква=лягушка
матем+ика=математика
Изначальная задача тоже решаемая в смысле есть решение задачи, но при этом множество решений пустое.
А теперь просчитайте варианты, если "o" — это запятая, разделяющая целую и дробную части )
В комментарии выше идёт речь о нерешаемости meow+meow=cat. Если "o" — запятая, тогда meow+meow=cat эквивалентно AB,C+AB,C=DEF. Например, 64,5+64,5=129.
Очевидно, что С=1, значит А=5, значит О=2. Но с другой стороны, если А=5, значит О должно быть нечётным, а мы уже выяснили, что О=2. Задача не имеет решения
Но я слишком туп для того, чтоб решить задачу полностью.