Задача на вероятность⁠⁠

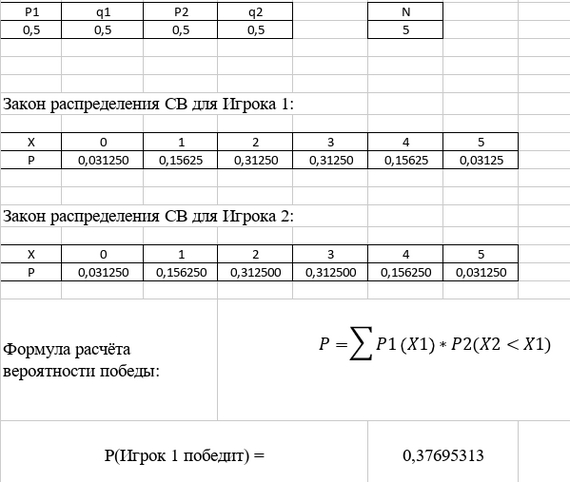
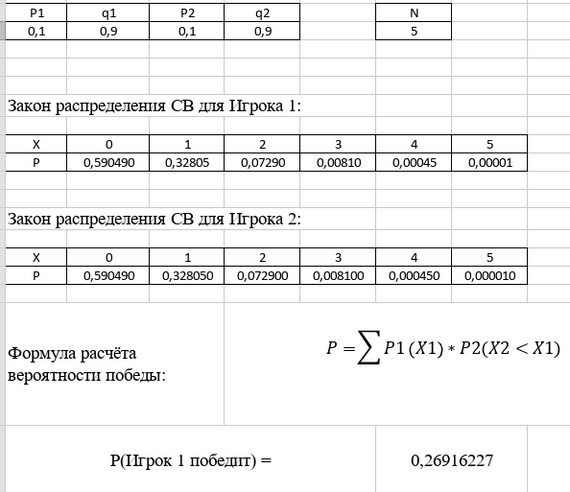
Условие задачи и ответ в картинке. Идея следующая: победителем становится тот, у кого больше попаданий, следовательно, нужно сложить все вероятности, при которых Игрок 1 набирает больше попаданий чем Игрок 2 (ничья не считается), а это равно произведению вероятности события P1 и суммы всех P2 таких, при которых значение СВ из второй таблицы (X2) меньше чем из первой (X1), о чём написано в формуле. Вопрос к лиге математиков следующий: верны ли мои рассуждения?

Смутил именно конечный ответ: всего около 14%, а когда вероятности попадания у обоих игроков равны, то ответ всегда варьируется в районе 25-37%, в общем, какие-то низкие проценты. Ведь даже если взять P1 = 0.8, а P2 = 0.9, то ответ будет 16,9%, хотя интуитивно кажется, что процент должен быть значительно выше.

За оформление заранее прошу прощения у знатоков экселя.

Когда вероятности равны:

И да, задачу я составлял сам. Жду критику или подтверждения...