Теорема Ферма. Помогите найти ошибку в решении.⁠⁠

Для начала вот вам лекция Савватеева о диофантовых уравнениях, с которой всё и началось

Лекция достаточно годная. В начале лекции рассказывается о том кто такой Диофант и чем он знаменит. Основное время в данной лекции уделено нахождению всех пифагоровых троек удовлетворяющих соотношению A^2 + B^2 = C^2 разными способами. (знаком ^ я буду обозначать степень числа, так как хз как с клавиатуры ещё её обозначать).

В этой лекции нас интересует алгебраическое решение. Оно начинается с 39:48 и заканчивается в 56:06.

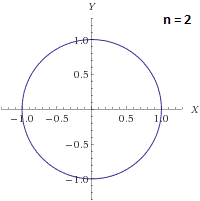
Итак, что мы имеем: мы нашли все рациональные точки на единичной окружности, то есть мы нашли все пифагоровы тройки (a, b, c рациональны и натуральны).

Пифагоровы тройки это частный пример теоремы ферма. Которая утверждает, что для

A^n + B^n = C^n нету решений в натуральных целых числах отличных от ноля для n>2.

Теорема ферма для четных n будет решена в начале следующей лекции( в прочем это не важно) поэтому ищем решения для нечетных n.

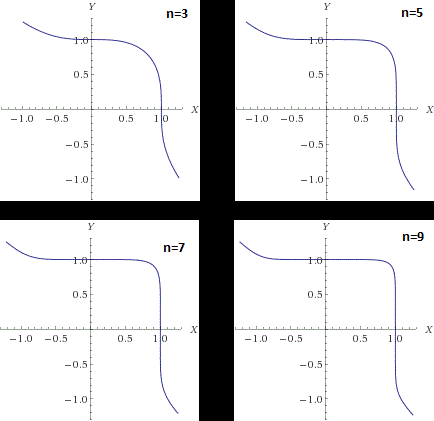
Рассмотрим графики Y^n + X^n = 1, где (Y = A/C; X = B/C) для разных n:

Вполне очевидно что при росте n график все дальше уходит от окружности, которой он является при n = 2.

Картинки графиков построены с помощью сайта wolframalpha

А теперь само решение:

!!! Ключевое утверждение - для n > 2; для того чтобы все решения для A^n + B^n = C^n ((A, B, C)- решения) были натуральны, они должны быть пифагоровыми тройками.

Доказательство ключевого утверждения

1) преобразуем A^n + B^n = C^n в Y^n + X^n = 1 (Такие что Y = A/C; X = B/C)

2) построим график для любого нечетного n > 2(Не суть для какого n; Для всех четных n теорема ферма решена)

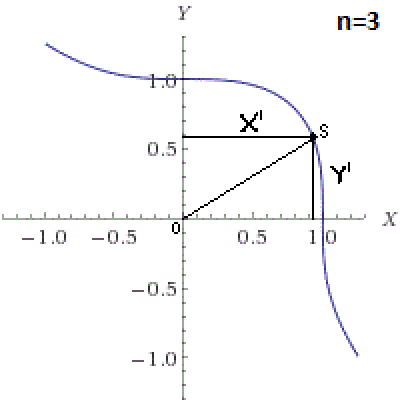
3) на этом графике возьмем любую точку (точку S) и проведем из неё касательную на оси абсцисс и ординат.

4)мы получим вертикальную длинну(скажем Y'), горизонтальную(скажем X') и длинну от нуля до самой точки(скажем OS).

5)то есть мы получили треугольник.

6)Что бы (Y'; X'; OS) были рациональны они должны быть в числе пифагоровых троек (все которые мы нашли ранее, см лекцию)

Ну то есть при умножении рациональных (Y'; X'; OC) на какоето рациональное число L мы попадаем в единичную окружность, где уже мы нашли все рациональные тройки.

Грубо говоря Любое решение (A^n + B^n = C^n) входит в множество решений (A^2 + B^2 = C^2).

Теперь решаем простую систему уравнений: {(A^n + B^n = C^n) ; (A^2 + B^2 = C^2)}

Самое простое решение - решение построением.

Опять делаем преобразование и строим окружность Y^2 + X^2 = 1; 

и график Y^n + X^n = 1.

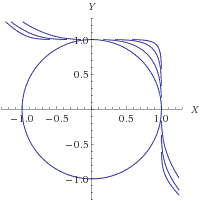
График при n=2;3;5;9;

Наглядно видно что для любого n > 2 эти два графика пересекаются исключительно в нулях (Y = 0 либо X = 0). А больше решений нет.

Заключение. Теорему ферма решали триста с лишним лет и лишь в 1994 году её таки решил Эндрю Уайлс с помощью эпилептических кривых (130 страниц доказательства), за что год назад получил Абелевскую премию.

300 лет её решали как великие математики так и дилитанты, и каждый раз в их решениях находилась ошибка.

Вот вам моё решение. Я уже второй день ищу в нем ошибку и не могу найти. Это превратилось в манию, психоз. Вобщем беда.. Надо выговориться.

Хорошо бы к математику какому нибудь бы пойти или на форум, но в последнее время тусуюсь только на пикабу. Поэтому делюсь доказательством с вами. Надеюсь вы либо найдете ошибку, либо подтвердите верность доказательства.