Простейшее устройство для измерения высоты солнца⁠⁠

Всем привет. Время от времени люди спрашивают, как можно убедиться в тех или иных постулатах базовой астрономии. Например, вы им говорите "угловой размер диска солнца и угловая скорость его перемещения по небу неизменна в течение дня", они вас спрашивают "а как это можно узреть?", а вы им берёте и рассказываете об элементарной конструкции, доступной в изготовлении практически любому заинтересовавшемуся.

Или например рассказываете вы об изолиниях солнца (1, 2), а человек парирует "а врёшь ты всё, солнце вообще почти в зените, а не на 60 градусах выше горизонта", ну или помягче: "всё замечательно, но как, собственно, измерить эту высоту?"

Обычно для таких целей люди предлагают поставить палку (гномон), измерить длину тени от неё и простыми вычислениями определить искомый угол, и теоретически они правы, но в реальности все эти измерения нужно делать с хорошей точностью (вертикально выставить гномон, горизонтально сориентировать площадку, на которую падает тень), чтобы суммарная погрешность составила менее 1 градуса. Несколько лет назад я помогал сыну делать работу (для школьной презентации), в которой измерялась траектория солнечной тени от небольшого столбика в течение дня (с отрисовкой на листе А4), и далее эта траектория анализировалась на предмет того, чтобы узнать координаты места проведения эксперимента. Отклонение по широте (это как раз компонента, отвечающая за высоту солнца) тогда составило от 0.5 до 1 градуса. Для школьной работы это конечно сгодилось, да и я помню про полуградусный угловой диаметр солнца, но у меня в голове засело - "надо найти способ измерения высоты солнца попроще и поточнее".

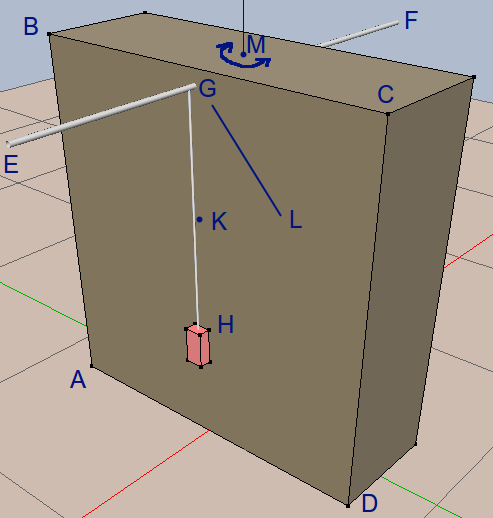
Сегодня я как раз хочу рассказать о таком способе, который проверил за последние недели. Установка делается буквально из подручного материала - коробка из-под бытовой техники, спица, лист А4. Схема установки выглядит следующим образом:

Не пугайтесь большому количеству букв - их я проставил для удобства дальнейшего описания. Всё на самом деле очень просто - нужно измерить угол между отвесом и направлением солнечной тени от спицы.

Подробнее:

1) берём коробку с прямыми углами (параллелепипед);

2) протыкаем её спицей EF в точке G и затем во второй (задней) грани коробки так, чтобы спица была приблизительно перпендикулярна передней грани ABCD (на этой стадии суб-градусные точности необязательны, поскольку вклад отклонений в дальнейшие измерения будет пренебрежим);

3) вблизи точки прокола G вешаем на спицу отвес GH (в моём случае это была подручная флешка на нитке);

4) помечаем точку К напротив нитки, на произвольном расстоянии от G (отрезок KG при этом становится вертикальным);

5) поворотом коробки по азимуту (вокруг вертикальной оси, см. точку М) добиваемся совмещения солнца с плоскостью ABCD (при этом тень от спицы GL - на грани исчезновения);

6) на произвольном расстоянии от G отмечаем точку L, лежащую на видимой солнечной тени спицы, и тут же помечаем точное время (узнать можно например через андроид-приложение ClockSync);

7) замеряем штангенциркулем (погрешность 0.1-0.2 мм) все три стороны треугольника KGL;

8) чтобы не мучиться с каждым опытом, обсчитывая его в калькуляторе, вбиваем все три стороны треугольника в эксель и вспоминаем теорему косинусов, из которой искомый угол KGL (зенитное расстояние солнца) составляет (если положить KG=a, GL=b, KL=c) величину φ = arccos[(a^2+b^2-c^2)/(2ab)].

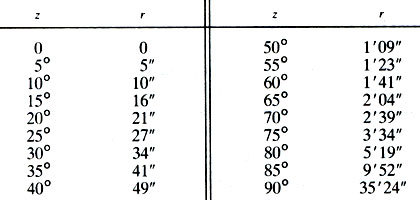
Далее мы можем сравнивать вычисленное значение φ с тем, которое ожидалось в соответствии с расчётом (по изолиниям из Google Earth, из планетария типа Stellarium, я скажем пользуюсь своей Day-night). Можно также сделать поправку r на рефракцию (z - зенитный угол, то есть 90 градусов минус высота солнца над горизонтом):

В моём случае погрешность метода (с учётом того, что стороны треугольника KGL лежали в пределах от 100 до 150 мм) по пяти измерениям в разное время и разные сутки не превысила 0.2 градуса (последовательные значения -0.08; -0.01; +0.15; +0.18; +0.08), что я считаю хорошим показателем, особенно если опять вспомнить про угловой размер диска солнца.

Вот как выглядел один из "измерительных" листков:

Надо сказать, что он не так уж помят, как выглядит. ) Просто при освещении в створ все неровности утрируются.

Итак, основная мысль, которой я хотел поделиться - я даже немного удивился, что таким простым способом можно добиться столь неплохой точности измерения высоты нашего светила (в два с лишним раза меньше его характерного углового размера).

К слову, с учётом скорости уменьшения высоты солнца в вечернее время в средних широтах (0.1-0.2 градуса в минуту) подобное измерение можно использовать и в обратную сторону - измерить время (если заранее сделать расчёт на этот день) с точностью 1-2 минуты.