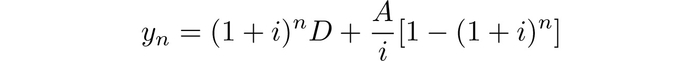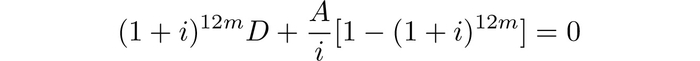Аннуитетный платёж - амортизация долга
В данной раздаче я собираюсь математически расписать принципы аннуитетных платежей, поскольку очень часто встречаются посты и комментарии на эту тематику.
Когда деньги занимают под процентную ставку r, общий долг увеличивается по тому же принципу, что и депозит, на который падают проценты по той же ставке. Амортизацией долга называется процедура выплаты долга, включая проценты, серией платежей. Обычно платежи имеют равный размер и совершаются в равные промежутки времени (ежегодно, ежеквартально или ежемесячно).
Предположим, что долг D, взятый под годовую ставку r, амортизируется за период m лет и выплачивается равными платежами, равными A, ежемесячно.
Пусть y(n) - остаток долга после n месяцев. Тогда y(n)-y(n-1) есть разница в долге в течение n-го года, и она состоит из процентов r/12*y(n-1), начисленных за n-й месяц за вычетом ежемесячного платежа. Обозначим i=r/12.
Тогда y(n)-y(n-1)=iy(n-1)-A.
Приводя подобные слагаемые и учитывая, что y(0)=D, мы получаем разностную задачу Коши
y(n)=(1+i)y(n-1)-A, y(0)=D.
Это уравнение имеет решение
Поскольку долг необходимо выплатить в течение m лет (т.е. 12m месяцев), нам нужно найти A так, чтобы y(12m)=0, т.е. получаем уравнение
Решая это уравнение, мы находим, чему должен быть равен ежемесячный платёж при честной процедуре амортизации:
Таким образом, мы можем рассчитать остаток долга после n месяцев.
В качестве примера приведу график при r=0.1 (10% годовых, i = r/12) , m=30 лет = 360 месяцев. Долг я буду считать равным 1 (условному числу), т.к. нас интересует скорость выплаты.
Итак, iy(n-1)/A - это отношение начисленных процентов за n-й период к постоянному платежу. Соответственно, мы можем построить график величины iy(n-1)/A.
Из графика как раз отчётливо видно, что самую большую долю проценты занимают в начальных периодах, а затем эта доля снижается.
Надеюсь, эта статья окажется кому-то полезной и поднимет уровень финансовой грамотности.