Закон Стиглера и эффект Джанибекова
Сегодня у нас в студии вторая часть, про эффект Джанибекова.
"Никакое научное открытие не было названо в честь первооткрывателя", написал Стивен Стиглер в своей книге. Сегодня этот факт известен как "закон Стиглера". Стиглер знал, про что писал, т.к. по его словам первооткрывателем закона Стиглера был Роберт Мертон.
Сам эффект Джанибекова вы можете наблюдать на видео ниже.
Эффект Джанибекова - это прекрасная иллюстрация т.н. "волчка Эйлера". Однажды Эйлеру стало очень интересно, как вращаются различные предметы, если их крутануть. Казалось бы, ну что тут сложного, как ты его закрутил, так он и будет вращаться? Да хрен там.
Пораскинув мозгами и накатив накатав немного диффуров, кто-то умный (возможно сам Эйлер, не знаю) сумел полностью описать вращение любого твердого тела. В частности, оказалось, что вращение вокруг большой и малой осей инерции устойчиво, а вокруг средней оси инерции - неустойчиво.
Без паники! Этот эффект можно прекрасно увидеть дома. С книжкой или айпадом. Но сначала - важное предупреждение для некоторых любителей применять физические законы куда попало! Теорему о неустойчивом вращении можно применять только к твердым телам. Вот краткая памятка:
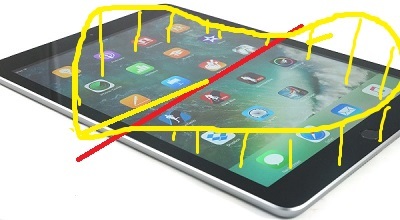
Возьмем айпад (не реклама) и закрутим его как на картинке, строго вокруг средней оси инерции, т.е. "ширины". Что будет?
А вот и нет. Если закрутить его идеально вокруг средней оси, ничего не будет. Т.е. ничего интересного не будет - он будет просто вращаться вокруг средней оси.
Но конечно же закрутить идеально вокруг средней оси инерции не получится- реальная ось вращения всегда будет чуть под углом. И вот тут начинается самое интересное. Но давайте сначала посмотрим на большую ось. Допустим, вы закрутили айпад вокруг большой оси инерции, но не совсем (желтым):
В первый момент времени айпад будет вращаться вокруг желтой оси - так, как мы его закрутили. Но! Потом ось вращения изменится. Если проследить траекторию оси вращения, то окажется, что она описывает окружность (точнее, эллипс):
Иными словами, вначале айпад крутился вокруг, скажем, дальней фиолетовой иконки. Но в какой то момент он будет крутиться вокруг дальней красной иконки. Потом опять фиолетовой, итд. Желтая ось вращения всегда будет двигаться, но всегда будет оставаться близко к красной оси - это и называется устойчивостью. Визуально будет казаться, что айпад просто крутится вокруг красной оси.
Тот же эффект происходит, если закрутить вокруг малой оси:
Реальная ось вращения будет "гулять" по айпаду, но всегда оставаться близко к малой оси. Но в этом случае гораздо проще увидеть это "гуляние" - если закрутить не очень аккуратно, то видно, как айпад будто бы колеблется из стороны в сторону.
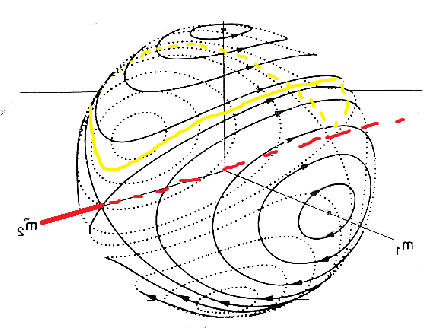
Все меняется, если вертеть вокруг средней оси инерции. Вот примерно такими американскими горками выглядят похождения оси вращения в этом случае (рисую как умею):
Или, чтобы было понятнее, как это выглядит в 3D, мысленно впишите айпад в сферу (хз, помогло ли):
Причем перемещение оси по желтой траектории неравномерно. Сначала ось долго тупит в районе начального положения, близко к красной оси. В этот момент нам кажется, что гайка/айфон просто крутится вокруг своей красной оси, и ничего не предвещает... Но потом ось довольно быстро перебегает в противоположную сторону. В момент перебегания вращение просходит вокруг упоротых осей (далеко от основных осей предмета) и потому выглядит хаотично (тот самый кульбит гайки/подброшенной книжки). Но к концу перебегания ось опять оказывается близко к красной оси - правда, с противоположной стороны предмета - что для нас выглядит, как смена направления вращения гайки.
(Еще одна попытка изобразить, как это выглядит. Поиграться можно тут - http://www.ialms.net/sim/3d-rigid-body-simulation/ , поставьте view - Poinsot construction (ellipsoid))
Все эти спецэффекты можно наблюдать, подбросив любой "кирпичеобразный" предмет с неодинаковой длиной-шириной-высотой, или вообще любой предмет с неодинаковыми моментами инерции, коим и является гайка в видео.
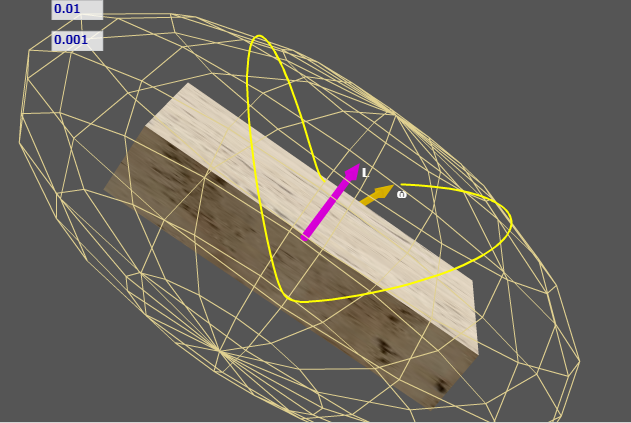
Ну и замечание напоследок: чтобы окончательно всех запутать (не я такая - жизнь такая), подчеркну, что желтые траектории - это траектории относительно самого предмета (т.е. где бы испачкался предмет, если бы ось вращения пачкалась). Это НЕ траектории оси в пространстве (т.е. где бы испачкался воздух, если бы ось пачкалась). Там все совсем печально. Можно для примера позалипать в это видео:
Ось вращения на этом видео подписана буквой w. Гуляя по предмету, она рисует на нем замкнутую кривую, как на картинке сверху. Но т.к. и сам предмет тоже движется, реальная траектория оси в пространстве оказывается довольно сложной.
Говорят, Эйлер был позитивным и добродушным мужиком, и думаю, что он бы только обрадовался, если бы узнал, что его теорема получила такое наглядное подтверждение, да еще и названное в честь российского космонавта Джанибекова. Но не будем забывать и того, кто все это начал!