Юбилейный 100ый пост про математику :-) Проблема Уилла Хантинга⁠⁠

Свой юбилейный 100 пост я хотел бы сделать для любителей математики и посветить его интересной проблеме о которой рассказывается в старом но хорошем фильме... и которую так легко и смешно раскритиковали на моем любимом канале Numberphile.

Good Will Hunting - Умница Уилл Хантинг

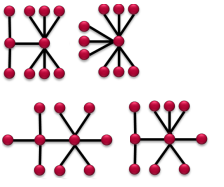
Нарисуйте все гомеоморфно несводимые деревья для размерности n=10.

Звучит страшно и непонятно. Но что же всё таки нужно сделать и так ли это сложно ?

Что такое дерево в данном случае ?

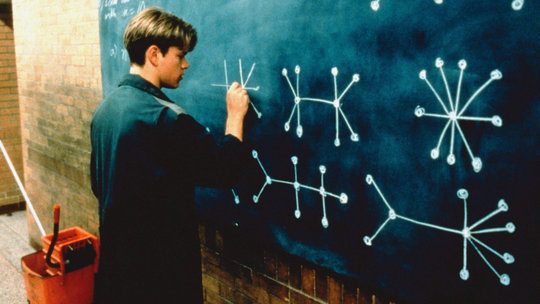
Дерево - это просто точки соединенные линиями но не имеющие замкнутых циклов - то есть никаких закрытых треугольников или квадратов.

Теперь разберемся то такое гомеоморфный ?

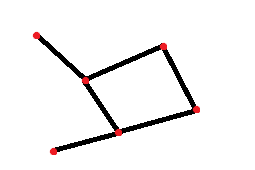
Это означает, что все симметричные или отзеркаленные деревья не считаются за новое дерево. А так же все деревья с одинаковыми узлами но с разными положениями веток тоже не считаются уникальными, а являются одним и тем же деревом.

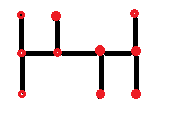
Ну и последнее - несводимые (или по английски "нередуктивные" ) деревья. Что же это такое?

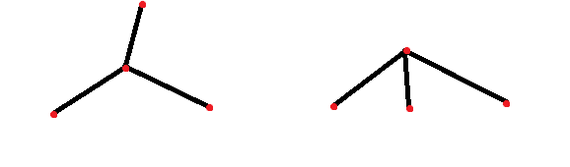
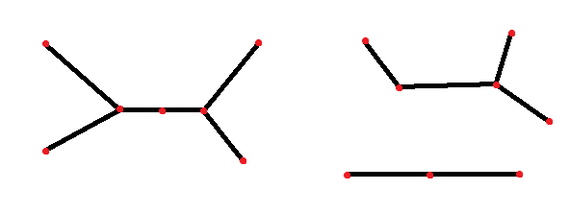
Это означает, что в данном дереве нет бесполезных (редуктивных) узлов, которые просто соединяют всего две ветки, но не являются разветвлением. В данных примерах из каждого дерева можно убрать узел, из которого исходит всего 2 ветки.

Вот и всё :)

Ничего сложного :)

Всем добра и знаний :) И спасибо за более 1000 подписчиков :)