Рисуем красивые фигуры 2.0
Этот пост является продолжением моего поста Когда нечего делать вечером.
Решил пойти дальше и вместо десктопного приложения запилить веб. Опубликовал на Heroku.
Адрес: http://draw-figure.herokuapp.com, можете пробовать!
Итак, вот что мы имеем.
Три пункта меню: Polygon Spiral, Polygon Spiral Group, Polygon Star.
Первые два пункта повторяют всё то, что было проделано в первом посте (напоминаю, там рисовались «спирали» из треугольников, посмотреть видео можно тут). Третий пункт предназначен для рисования новой фигуры (буду далее называть ее «звезда»).
Теперь обо всём по порядку.
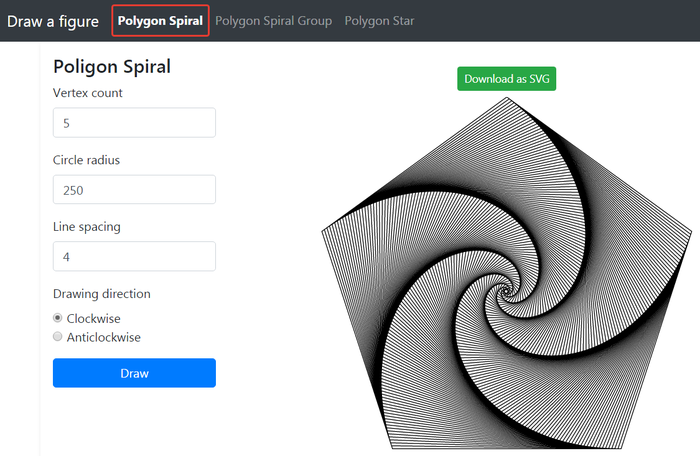
1. Polygon Spiral
Рисует «спираль» на правильном многоугольнике.
Для построения необходимо указать 4 параметра (здесь и далее размерность – пиксели):
a. Vertex count – количество вершин многоугольника (целое число от 3 до 50);
b. Circle radius – радиус описанной около многоугольника окружности (целое число от 1 до 5000);
c. Line spacing – расстояние между соседними линиями, образующими «спираль» (дробное число, большее либо равное 1.5);
d. Drawing direction – направление рисования «спирали» (по часовой или против часовой стрелки).
2. Polygon Spiral Group
Позволяет на одном изображении рисовать несколько «спиралей», в основе которых лежат произвольные (не обязательно правильные) выпуклые многоугольники.
Тут всё немного сложнее. Необходимо указать описание желаемого изображения.
Описание состоит из нескольких строк.
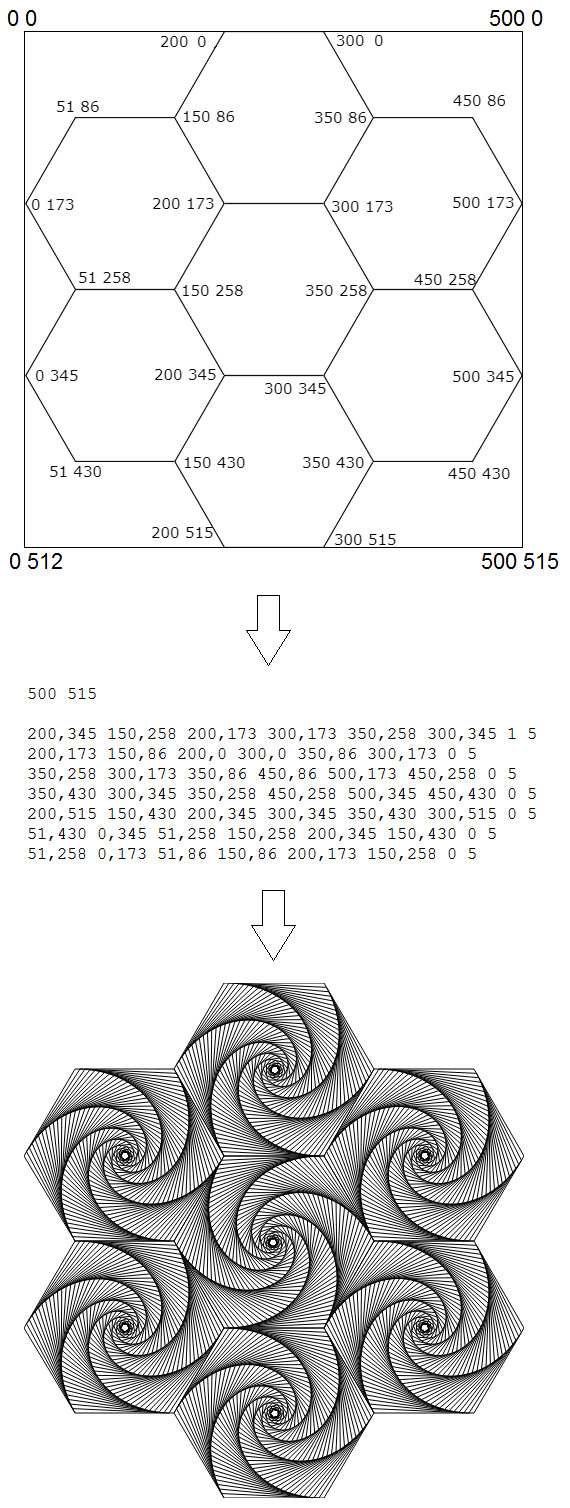
1-я строка содержит два положительных числа, разделенных пробелом, – ширину и высоту изображения.
Далее допустимо произвольное число строк. Каждая из них описывает многоугольник в следующем формате: x1,y1 x2,y2 ... xn,yn d s.
Здесь:
x1,y1 x2,y2 ... xn,yn – координаты вершин многоугольника в порядке обхода;
d – направление рисования «спирали» (0 – по часовой стрелке, 1 – против часовой стрелки);
s – расстояние между соседними линиями, образующими «спираль» (дробное число, большее либо равное 1.5).
Небольшой графический комментарий для ясности:
Также можно попробовать разные примеры, нажав на кнопки Case 1, Case 2 и Case 3.
3. Polygon Star
Вот принцип рисования части «звезды»:
Программа позволяет рисовать «звезду» на правильном многоугольнике.
Для построения необходимо указать 3 параметра:
a. Vertex count – количество вершин многоугольника (целое число от 3 до 100);
b. Circle radius – радиус описанной около многоугольника окружности (целое число от 1 до 5000);
c. Split count – на сколько частей разбивается радиус окружности (целое число от 0 до 500).
Несколько интересных примеров:
На этом всё! Еще раз, адрес приложения: http://draw-figure.herokuapp.com. Если у вас есть какие-нибудь интересные идеи – предлагайте!