Прямоточный пульсирующий детонационный двигатель нового типа
Как это работает? (По простому!)
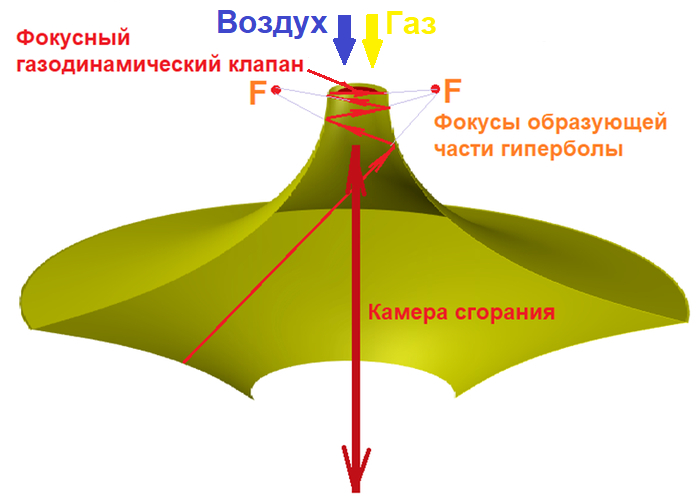
Двигатель выглядит как две воронки (одна из которых немного обрезана), соединённые вместе. Это псевдогиперболоид 2-го порядка, фигура из мира Геометрической Волновой Инженерии (ГВИ) псевдоповерхностей переменной отрицательной кривизны с одной верхней фокальной зоной концентрации волновой энергии . Нижняя фокальная зона концентрации волновой энергии псевдогиперболоид 2-го порядка - обрезана.
Топливо и воздух втягиваются сверху, загораются в центре — БАХ! 💥 Взрывная волна мчится по стенкам, пере отражается и создаёт в верхней зоне концентрации волновой энергии - волновой барьер . Это, как невидимая пробка, которая в момент БАХ! 💥 не даёт газикам вырваться туда, откуда втягивалось топливо и воздух. Вместо этого газики с силой вылетают вниз, создавая тягу. Барьер исчезает, и всё повторяется — до 300 раз в секунду, как космический ритм! 🎵
Почему это взрывает мозг?
Не убиваемая надёжность: Ни одной движущейся детали — только форма управляет потоком! 💪
Компактный масштабируемый монстр: Идеален для любых размеров, что недоступно для дефлаграционной классики ПуВРД 🛰️
Мощь на максимум: Меньше потерь энергии, чем у бесклапанных ПуВРД, — каждый импульс бьёт точно в цель! ⚡
Следующий шаг — псевдогиперболоид 3-го порядка с кольцевым волновым барьером, который сделает двигатель ещё мощнее и эффективнее! 🚀 Следите за публикациями, следующая публикация - это спиновый детонационный на основе псевдогиперболоид 3-го порядка.
PS:
Это не апгрейд известных дефлаграционных бесклапанных ПуВРД — это новый класс технологий для авиации, космоса и энергетики 🚀.