Нюансы Python #2: деление и остаток⁠⁠

Вы отлично знакомы с арифметическими операциями в Python? Тогда попробуйте вычислить результат следующих выражений, не запуская интерпретатор:

5 // -2
-5 // 2
5 % -2
-5 % 2

Если у вас получилось -3, -3, -1 и 1, то снимаю перед вами шляпу. А если нет, то добро пожаловать в основную часть поста, где мы подробно разберём, почему получился именно такой результат.

Прочитать материал в более удобном виде, с форматированием и интерактивными примерами кода, можно здесь.

Про разные подходы

В математике «поделить a на b с остатком» означает «найти такие числа q и r, что будет выполняться равенство b*q + r = a».

a - делимое;

b - делитель;

q - неполное частное;

r - остаток.

Например:

11 / 4 = 2, остаток 3.
4 * 2 + 3 = 11

7 / 2 = 3, остаток 1.
2 * 3 + 1 = 7

14 / 5 = 2, остаток 4.
5 * 2 + 4 = 14

А если остаток отрицательный?

В математике принято считать, что остаток должен быть неотрицательным, то есть должно выполняться неравенство 0 <= r < b. Но ведь физически никто не мешает нам сделать так:

11 / 4 = 2, остаток 3
11 / 4 = 3, остаток -1

Равенство b*q + r = a по-прежнему выполняется, а остаток по модулю по-прежнему меньше делителя.

Конечно, если делимое и делитель положительные, то такой выбор остатка выглядит странновато. Но давайте поработаем с отрицательными числами:

11 / -4 = -2, остаток 3
11 / -4 = -3, остаток -1

Какой из этих вариантов правильный? На самом деле, оба. Просто существуют разные подходы к делению с остатком:

- деление с округлением вниз;

- евклидово деление (привычное, как в математике).

Деление с округлением к нулю

«Округлить a к нулю» означает взять первое целое число, которое идёт на числовой прямой сразу после a по направлению к нулю.

Давайте поделим 11 на -4 и -11 на 4. В обоих случаях получится -2.75. Если округлить к нулю, то будет -2.

Теперь посчитаем остаток. Из формулы b*q + r = a выводится, что r = a - b*q. В первом случае: r = 11 - (-4)*(-2) = 11 - 8 = 3, во втором случае: r = -11 - 4*(-2) = -11 - (-8) = -3.

То есть если мы округляем результат деления к нулю, то получаем следующую картину:

11 / -4 = -2, остаток 3
-11 / 4 = -2, остаток -3

При делении с округлением к нулю знак остатка всегда совпадает со знаком делимого, а от знака делителя вообще никак не зависит.

Деление с округлением вниз

«Округлить a вниз» означает взять первое целое число, которое идёт на числовой прямой сразу после a по направлению к минус бесконечности.

Если мы округляем результат деления вниз, то получаем следующую картину:

11 / -4 = -3, остаток -1
-11 / 4 = -3, остаток 1

Теперь знак остатка совпадает со знаком делителя, а от знака делимого не зависит.

Евклидово деление

Это классический подход, который используется в математике. В нём остаток должен всегда быть положительным, а куда для этого нужно округлять неполное частное - уже не имеет значения.

11 / -4 = -2, остаток 3
-11 / 4 = -3, остаток 1

Какой подход используется в Python?

На интуитивном уровне многие считают, что деление нацело (оператор //) сводится к отбрасыванию дробной части. То есть из 2.4 получаем 2, а из -2.4 получаем -2. Это деление с округлением к нулю, и остаток считается соответствующим образом, то есть его знак совпадает со знаком делимого. Во многих языках, от Pascal до C#, используется именно этот подход.

Но создатель Python, Гвидо ван Россум, выбрал другой подход: результат целочисленного деления всегда округляется вниз. За использование деления с округлением вниз в информатике также выступал Дональд Кнут, известный математик и автор книги «Искусство программирования».

Соответственно, в Python -5 // 2 - это -3, а не -2. Знак остатка при этом совпадает со знаком делителя.

Почему именно деление с округлением вниз?

Всё дело в ситуациях, в которых на практике используются операторы // и %.

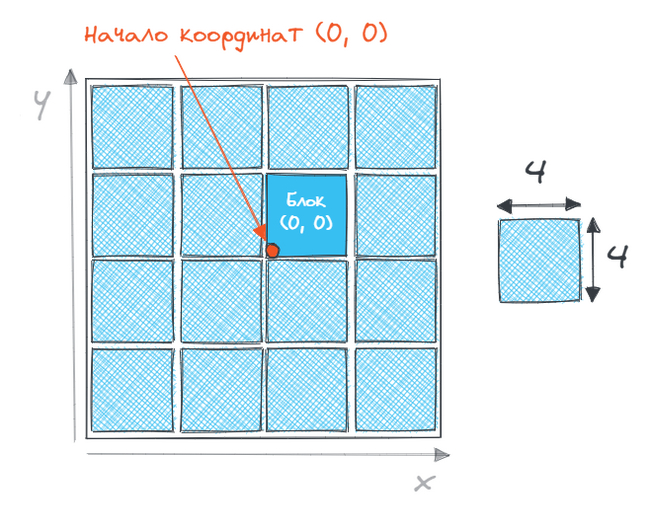
Например, представьте себе поле размером NxM пикселей. Оно разбито на блоки размером 4х4 точки каждый.

Будем работать со следующими сущностями:

2. Номер конкретного блока. Например, блок (0, 0) - это тот, в левом нижнем углу которого находится начало координат. Справа от него блок с позицией (1, 0), а сверху - (0, 1);

3. Координаты точки внутри блока. Если ширина блока - 4х4, то координаты точки внутри блока могут меняться от (0, 0) (нижний левый угол) до (3, 3) (верхний правый угол).

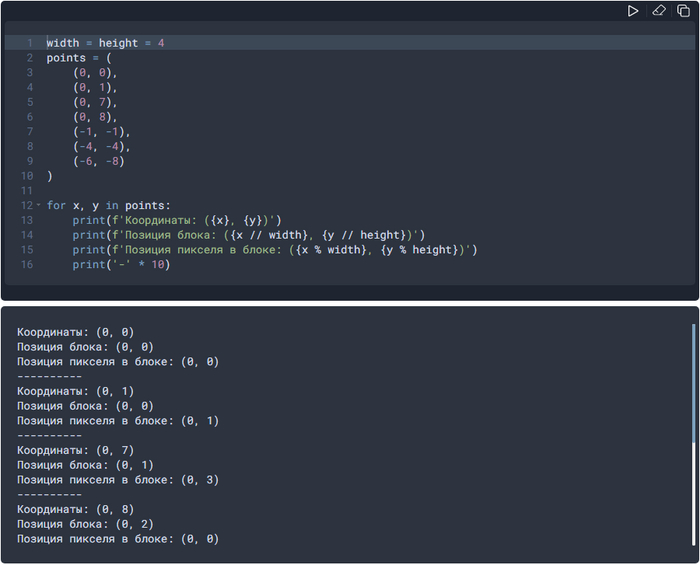
И теперь представим, что у нас есть координаты какой-то точки на поле, например, (-38, 11). Как узнать, в каком блоке находится эта точка и какую конкретно позицию внутри блока она занимает? Довольно легко, если в языке используется деление с округлением вниз:

Все результаты не влезли в скриншот, к сожалению. Запустить этот код онлайн можно здесь.

Обратите внимание на то, что с отрицательными координатами всё работает абсолютно корректно. А если бы использовалось деление с округлением к нулю, то для координат (-6, -8) мы получили бы некорректные результаты:

Координаты: (-6, -8)
Позиция блока: (-1, -2)
Позиция пикселя в блоке: (2, 0)

Очевидно, что координата x: -6 никак не может находиться в блоке, имеющем позицию x: -1, потому что ширина блока - 4 пикселя.

Какой подход лучше?

Любой.

Цель статьи не в том, чтобы сказать, что в Python используется хороший или плохой подход. Споры на тему того, как нужно правильно делить, идут уже давно, и навряд ли завершатся в обозримом будущем. Гвидо ван Россум и Дональд Кнут считают, что в программировании удобнее использовать деление с округлением вниз, а другие не менее именитые программисты могут считать, что лучше использовать деление с округлением к нулю или даже евклидово деление.

Поэтому просто запомните, что в Python при делении с остатком результат округляется в меньшую сторону, а не к нулю, и что остаток всегда имеет тот же знак, что и делитель.