Неправильные задачи
В последнее время на страницах Русской службы BBC примерно раз в неделю под рубрикой "Зарядка для ума" публикуются загадки. Но так ли эти они умны? Процитирую дословно две из них:
1. Какого цвета медведь? http://www.bbc.com/russian/other-news-41001479
Вы отправились на задание. Вы проехали 5 км на юг, затем 5 км на запад, затем 5 км на север и оказались в том же месте, откуда начали свой путь.
Во время своего путешествия вы видели медведя. Какого цвета он был?
2. Угадайте недостающее число. http://www.bbc.com/russian/other-news-41112029
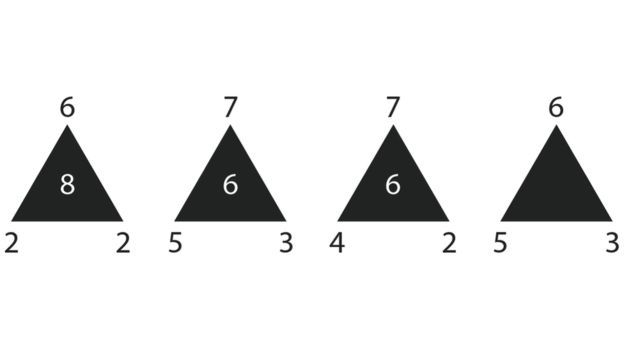
Какое число нужно вписать в пустой треугольник на картинке?
Теперь я скопирую с сайта BBC длинную картинку-заставку, которую они вставляют между задачей и её решением. Смысл этой картинки исключительно в том, чтобы дать читателю возможность поразмыслить немножко над задачей, а не прочесть случайно ответ сходу, по инерции.
После картинки я приведу ответы на эти 2 загадки и расскажу, что же с ними не так.
Вот какие ответы предлагает РС BBC, ссылаясь на авторов этих задач:
1. Белый
2. 3
Вот как они объясняют решение, цитирую также дословно:
1. Единственное место на Земле, где вы можете проехать 5 км на юг, затем 5 на запад, затем 5 на север и оказаться там, откуда вы отправились в путь, это Северный полюс.
На Северном полюсе обитают только полярные мишки, а они белого цвета.
2. Если из числа над треугольником вычесть число слева от него и умножить на число справа от треугольника, то получится число внутри него.
И вот, что с этими задачами не так:
1. Северный полюс - не единственное место, проделав из которого равные пути сначала на юг, затем на запад и затем на север, Вы окажетесь в точке старта. Даже если принять глагол "проехать" из условия задачи, как непременное требование находиться всё время на поверхности Земли (а не, допустим, в её центре, где понятия "Запад" попросту не существует), найдётся ещё бесконечное количество мест, в которых первая часть условия выполняется. Возьмите любую точку, удалённую от Южного - не от Северного, а именно от Южного полюса - на те самые 5 км плюс ещё 5/2πN км, где π - это число Пи, а N - любое целое число. Проехав из этой точки 5 км на юг, мы окажемся в точке на параллели длиной 5/N км, 5-километровое путешествие по которой через ровно N витков вокруг полюса вернёт нас в эту же точку, а ещё 5 км на север - в точку старта.
Что? В Антарктиде медведи не водятся? Вообще никакие? Не беда! В условии же не сказано, что мы живьём встретили медведя и непременно дикого. Там сказано "увидели". Увидеть можно любого медведя и где угодно, его даже не обязательно туда привозить, достаточно вытащить из кармана его фотку.
И вот какой урок из этого следует извлечь тому, кто хочет сочинять хорошие задачи: необходим тщательно выверенный баланс между слишком расплывчатым условием, допускающим различные толкования, т.е., различные решения и условием слишком жёстким и подробным, поскольку в таком решении внимательный читатель углядит подсказку, резко упрощающую задачу.
2. Существует ещё бесконечное количество функций таких, что f(6,2,2)=8; f(7,5,3)=6 и f(7,4,2)=6. Вот одна из них: f(a,b,c)=(a%2)*3*(b-c)+((a+1)%2)*2*(b+c), где "%" - операция "Остаток от деления". Говоря текстом, если верхнее число чётное, то берём удвоенную сумму нижних чисел, а если нечётное - то их утроенную сумму.
И да, эта функция для четвёртого треугольника даст отнюдь не 3, а ажно 16. В условии же не было сказано "цифра", там было сказано "число", а число имеет полное право быть двузначным.
Впрочем, даже будь в условии сказано "цифра", а не "число", это не спасло бы автора от решения, предложенного в комментариях Николаем Лисенко: сумма верхнего ряда цифр - 26, сумма нижнего ряда - 26, значит, сумма цифр внутри треугольников тоже должна равняться 26, а значит, искомое число - 6.
Второй урок таков: избегайте задач на поиск закономерностей в числовых рядах, т.к. вам самим может не хватить ни времени, ни познаний в математике на то, чтобы сформулировать условие достаточно жёстко.
И вот вам третий урок: мы все, надеюсь, знаем, что у любой сколь угодно сложной задачи есть простое и интуитивно-понятное неправильное решение. Но многие постоянно забывают о том, что найденное простое решение, даже если оно верное, может оказаться не единственным правильным решением.