Нелинейный прогресс, производственная функция и котик с печеньем
Производственная функция - это математическая модель, которая отражает взаимосвязь между единицами затрат на входе и результатами на выходе. Другими словами, она отвечает на вопрос: “Стоит ли овчинка выделки?”.
Разберем на котиках, как работает линейная и нелинейная производственная функция.
Котик Василий печет печенье на продажу. Количество печенья зависит только от часов работы. В данном случае у нас линейная производственная функция. Чем больше котик работает, тем больше печенья он приготовит. Другими словами, объем выпуска будет увеличиваться на одну и ту же величину для каждой единицы затрат.
Если немного усложнить производственную функцию и включить туда оборудование, которое использует котик, функция превратится в нелинейную.
Например, Василий купил новую печь, благодаря которой может выпекать в час в 2 раза больше печенья. Производство стало более эффективным. Объем выпуска увеличился, но не прямо пропорционально.
Каждая дополнительная единица ресурса добавляет все меньше к выпуску. Котик не может работать на двух печах одновременно. Мощности будут простаивать, отдача снизится. “Больше” не всегда значит “лучше”.
Люди считают, что есть прямая зависимость между ресурсами и результатом. Все как в линейной производственной функции. Чем больше котик работает, тем больше печенья он приготовит.
Наши интуитивные реакции исключительно линейны (однонаправлены). Рассмотрим нашу жизнь в ее простейших проявлениях: в ней действие и результат тесно связаны. Вам хочется пить, вы пьете, и вода утоляет жажду…
Более того, мы полагаем, что, если, скажем, между двумя переменными величинами есть причинно-следственная связь, прибавка к одной величине обязательно повлечет за собой прибавку к другой. Наш эмоциональный аппарат настроен на восприятие линейной причинности. Например, считается, что, занимаясь каждый день, ты выучишь больше, то есть результат будет пропорционален затраченным усилиям.
Черный лебедь. Насим Талеб.
В современном мире правят нелинейные зависимости. Представьте себе мост. Основная задача моста - помочь Вам в преодолении препятствия. Неважно сколько времени, сил и кирпичей Вы вложите в это сооружение. Пока мост не перекроет реку, яму, канаву или ущелье - его полезность равна нулю. Кроме того, добавление новых сегментов после того, как уже мост переброшен через препятствие, никак не увеличит пользу от моста..
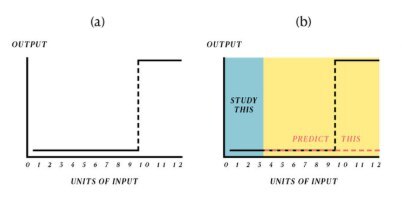
Производственная функция для моста представляет собой ступенчатую функцию. Первые 9 сегментов никак не влияют на “выпуск итоговой продукции”. Мост не завершен, значит он бесполезен. После монтажа последней части, мостом уже можно пользоваться, его польза достигает сразу максимума.
Если бы мы оценивали “потенциальную доходность”моста, используя только первые 9 сегментов, то картина была бы неутешительная. Мы уже вложили столько ресурсов, а отдача нулевая… Наша линейная производственная функция показана на рисунке b.
Все знают для чего нужны мосты, и как они работают. Но как часто мы ожидаем линейных результатов от нелинейной производственной функции в других сферах нашей жизни?