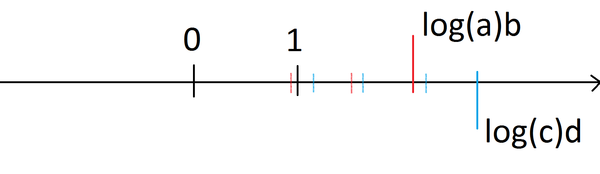Математический анализ и алгоритм И. С. Сергеева⁠⁠

МНОГОБУКАФ, матанализа, программирования и мало практического смысла.

Здравствуй, пикабу

Сегодня я хочу рассказать вам о том, как заставить половину класса врубать свои компьютеры на ночь перебирая числа (и нет, не майнинг)

В общем, учился 10 класс, учился, как тут приходит учитель по мат анализу и рассказывает тему "Алгоритм И. С. Сергеева для сравнения двух логарифмов"

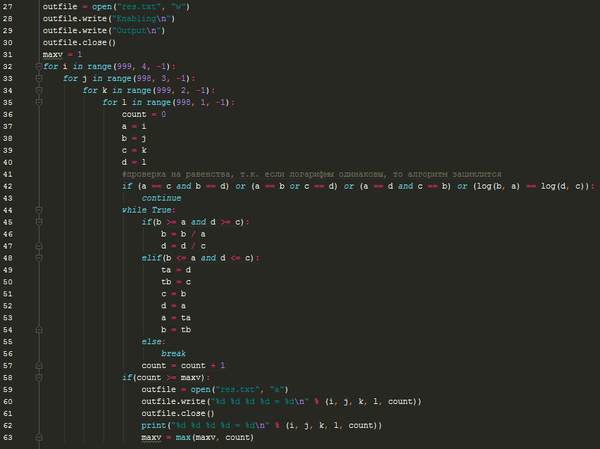
Собственно, вот он сам

(результат очевиден, так как между логарифмами можно вставить число 1).

И добавляет: "У меня был ученик, который нашел среди трехзначных чисел a, b, c, d такие, что этот алгоритм работал более 4000 раз!" - (Позже мы все поняли, что он где-то ошибся) - "И кто найдет такие числа, что алгоритм будет работать больше, поставлю 5 за теоретическую часть коллоквиума".

Я в этот момент не особо был заинтересован, так как, в принципе, мог все выучить, но вот мои одноклассники загорелись этой идеей. (Наш класс ориентирован на информатику, так что абсолютно все худо-бедно, но умеют программировать, некоторые даже очень хорошо)

Надо сразу сказать, что сразу же были найдены числа типа 999 998 998 997, на которых алгоритм выдавал >6000 действий, так что цель уже была найти число, на котором алгоритм работал бы больше всего.

В итоге получилось 3 группы:

1. Перебиратели

Надо найти числа? Дак давайте их переберем! Да, все правильно, они просто решили перебирать 1000^4 чисел, среди которых (в среднем) по 1000 действий, получается 10^15...

Короче говоря, именно у них компьютеры работали круглосуточно, считая эти числа.

Я приведу свой код на питоне, который выполнял именно это (да да, питон и быстродействие):

По началу, они первые нашли число, которое было больше других, если мне не изменяет память, это было 46603, а искали они его два дня

2. Цепные дроби

К сожалению, тут я могу быть неточен, так как не до конца понял рассказы одноклассников

Если вы откроете еще раз фотографию с алгоритмом, вы заметите слова про цепные дроби, и действительно, алгоритм схож с раскладыванием значения логарифмов в цепные дроби, пока они не будут различны, за счет этого можно как минимум получить приблизительную оценку количества действий (может быть и точное количество, поправьте меня, если я неправ).

В итоге, такая вещь работает (по словам одноклассников) быстрее, чем сам алгоритм.

Эта группа пришла позже в игру, но(!) она единственная нашла максимальное значение как минимум среди 1/3 вариантов (а то и всех, об этом немного дальше), а так же первая нашла близкие значения (максимальное порядка 74 тысяч, близкие - порядка 73 тысяч).

Я бы привел код одноклассника на питоне, но боюсь, что вы там ничего не поймете, так что просто скину его в архив в конце поста.

3. Математики

"Хм, а есть какая нибудь зависимость между a, b, c, d и количеством шагов?" спросили себя математики, каким то образом попавшие к нам в информаты. Если посмотреть на алгоритм, то он схож на "движение" чисел по числовой прямой, пока между числами нельзя вставить единицу:

Второй же шаг выполняется только тогда, когда оба числа (красное и синее) оказываются левее 1. Он "перемещает" их вправо и уменьшает расстояние между ними.

И математики придумали такую вещь (не спрашивайте меня, как):

Нам, оказывается, нужно перебирать не все числа, а только те, между логарифмами которых расстояние меньше 1e-6. И они были чертовски правы (но об этом чуть далее).

Соответственно, это существенно снижает перебор, а просто перебрать все числа (10^12) на современном компьютере займет около 15 минут!

И спустя время, они пришли с несколькими числами на 73 тысячи (максимум, который я смог найти, напоминаю, 74 тысячи)

Истина

Но я же не мог оставить вас вот так вот, с какими то приблизительными результатами, результатами перебора нескольких процентов от общего количества, какими то цепными дробями, откуда то взявшимися, и не очень понятной теоремой, пускай и, может быть, вполне правильной.

Придя домой из общежития, я запустил свой компьютер с AMD R9 290, загуглил OpenCL и решил посчитать все на видеокарте (благо, данный перебор идеально для этого подходит).

В общей сложности, мне бы потребовалось ~21 час на полный перебор, но я устал не гаматься слушать гудение вентиляторов уже вечером, так что перебрал только ~1/3, все b, c, d, для a от 999 до 700.

Файлик с результатами, куда я записывал числа только если количество действий было больше 1000, к этому моменту, уже весил ~200 мегабайт.

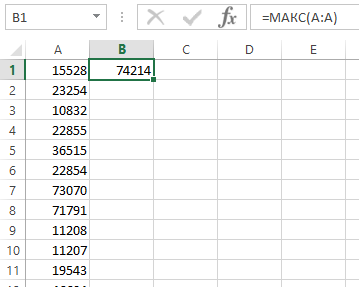
Итак, максимальное количество действий среди этих чисел...

(приблизительно) 74214! Его нашла только вторая группа.

А теперь, раз есть результаты, можно поделать всяких графиков.

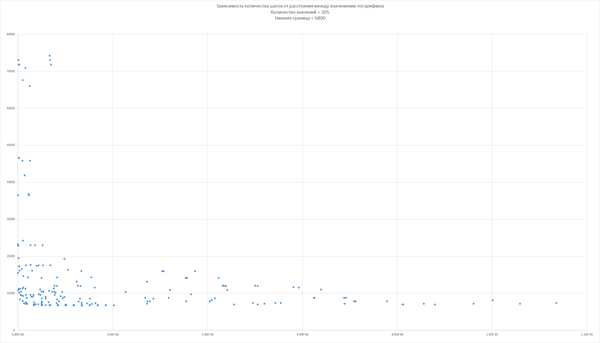
Итак, то, о чем говорила третья группа: зависимость количества шагов от разности логарифмов: (все фуллсайзы будут в архиве)

Здесь прекрасно (даже с таким качеством) видно, что вторая группа была абсолютно права. Напомню, что она нашла несколько чисел с результатом ~73 тысячи.

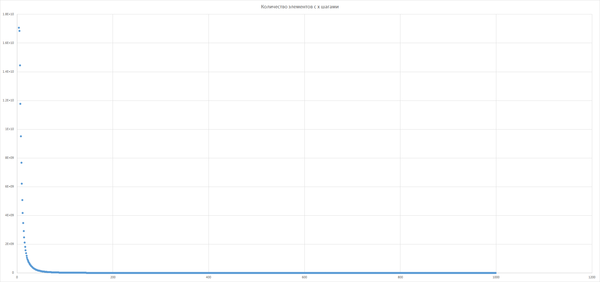
ОБОЖЕМОЙ, Мы же забыли про числа, результат которых меньше 1000! Ан, нет. Я просто записывал их количество в отдельный файл, график (пришлось выкинуть первые 4 элемента, так как они ну совсем не в тему)

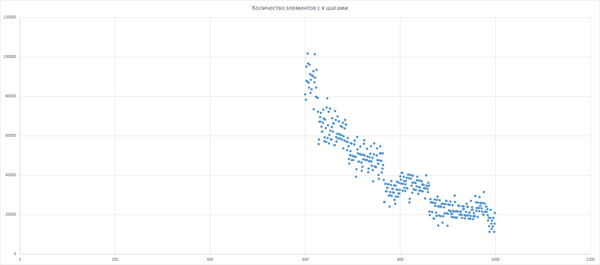
Увеличим область с 600 элементов

Просто красивые графики.

Вывод:

Что мне это дало? Да практически ничего, научился считать на видеокарте разве что.

Зачем я это делал? Просто так, было интересно найти максимум и проверить теорию третьей группы

Зачем я опубликовал это сюда? Потому что на хабре это точно не будет интересно, а поделиться хочется.

Кому поставили в итоге 5? Поставили человеку из первой группы, который показал число на 73 тысячи. Почему ему, а не тому, кто нашел 74к? "Потому что он усердный, встретил меня внизу (у входа в школу), ждал меня с самого утра" (С) Препод.

Ссылки на файлы:

Графики, некоторый код и часть результатов: https://www.dropbox.com/s/ffmrvaxksii3u7v/matan.rar?dl=0

Файл с результатами:

a b c d = колво_шагов

https://www.dropbox.com/s/29n6v84rw45otvb/res0.rar?dl=0

(сжат, архив 13 мб, сам файл почти 200 мб)