Кривизна Земли⁠⁠

Попался мне сегодня пост с картографическими проекциями нашей планеты,

(https://pikabu.ru/story/treniruem_mozg_na_proektsiyakh_zemli...)

а в посте комментарий со ссылкой на гневные тирады юного плоскоземельца.

Парень называл "теорию" сферической земли глупостью, и в качестве доказательства своих убеждений предлагал нам выглянуть в окна своих хрущёвок и убедиться что никакого шара на улице нет. Вообще, агрумент "от очевидности" довольно распространён среди плоскоземельцев, и как мне кажется, развенчанию состоятельности этого аргумента критики уделяют недостаточно внимания. Во исправление этого упущения, я попытаюсь объяснить почему земля за окном не слишком похожа на шар.

Для этого мне придётся соорудить цельнометаллический макет планеты в натуральную величину.

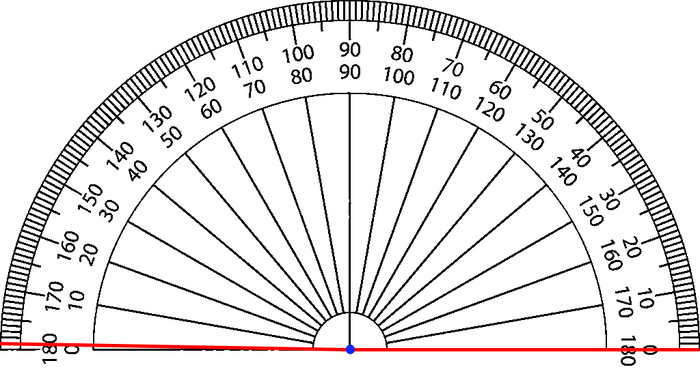
Итак, знакомьтесь: это транспортир.

Как вы могли заметить, на транспортире я изобразил красным цветом два отрезка, находящихся под углом в 1° друг к другу.

Чтобы транспортир не мешал вам разглядеть угол между отрезками, я уберу транспортир с рисунка. Останется только сам угол:

(Сначала я хотел убрать синюю точку, но потом решил что без неё не только лишь все смогут понять в каком именно месте соединяются отрезки.)

Итак, у нас есть два отрезка и угол в  1° между ними. Логично, что если мы достроим ко второму отрезку третий, тоже под углом в один градус, то угол между первым и третьим будет равен уже двум градусам. Таким образом, достроив один за другим 360 отрезков равной длины, мы получим замкнутую геометрическую фигуру -- трёхсотшестидесятиугольник.

Вот его-то (трёхсотшестидесятиугольник) я и использую в качестве экватора своей макетной планеты. Для простоты, планета будет не сферической, а цилиндрической (эффект искривления поверхности тот же, а моделировать проще), так что поверхность планеты будет состоять из 360 абсолютно плоских металлических плит, с углом в один градус в местах их стыковки.

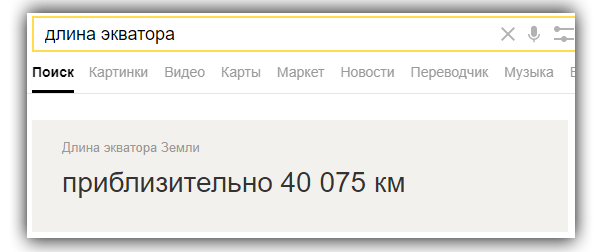
Но какого размера должны быть эти плиты? Погуглим.

В нашем случае, общая длина экватора будет равномерно распределена между длинами всех плит, коих, напоминаю, у нас 360. То есть длина отдельной плиты составит 40075/360, или, примерно 111км.

Сто одинадцать километров -- это много?

Я хожу с максимальной скоростью в шесть километров в час. Да, я замерял по карте.

Предположим, что некий Анонимус ходит с вдвое меньшей скоростью -- 3 км/ч. Чтобы пройти 111 километров, ему понадобится всего-то 37 часов безостановочной ходьбы.

Теперь отправим нашего Анонимуса в пешую экскурсию по экватору нашей макетной планеты, с целью обнаружения искривления её поверхности.

Первые сутки пути Анонимус будет удивляться тому, что поверхность нашей планеты идеально ровная, плоская как заркало. Ему даже начнёт казаться что мы его обманули и отправили на плоскую планету. Но затем, на вторые сутки, спустя больше 30 часов после начала путешествия,

он вдруг обнаружит, что поверхность планеты действительно имеет  изгиб.

Вот такой: