Изучение атмосферной рефракции с помощью высотных строений на горизонте
Всем привет. Месяц с лишним позанимался темой пригоризонтального наблюдения за удалёнными высотными объектами, численно смоделировал атмосферную рефракцию, сравнил результаты наблюдений с расчётом, и хочу рассказать вам сегодня о том, что из этого получилось.
Особенность окологоризонтальных наблюдений состоит в том, что чем ближе к горизонту расположен наблюдаемый объект, тем больше проявляется непрямолинейное распространение света. Такое явление называется атмосферной рефракцией и объясняется тем, что плотность воздуха, а вместе с ней и показатель преломления (ПП), уменьшается с высотой над поверхностью Земли (напомню, показатель преломления среды - это во сколько скорость света в этой среде меньше, чем в вакууме).
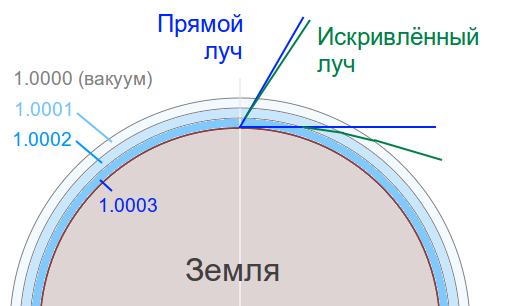
Давайте схематично рассмотрим это явление:
На картинке представлена модель планеты в сечении и несколько слоёв атмосферы, с показателями преломления условно 1.0003 (у поверхности планеты), и далее уменьшается с высотой, с шагом 0.0001, до космоса, в котором ПП строго равен 1.0000. Эта картинка, понятное дело, и не в масштабе, и весьма условна по количеству слоёв, на самом деле при численном моделировании вы можете разбивать атмосферу на произвольное количество слоёв, плотность которых убывает примерно по экспоненциальному закону от высоты.
Оценим по закону Снеллиуса, насколько отличается отклонение луча, падающего на границу сред под большим углом (в нашей картинке это горизонтальный луч, уходящий вправо), от отклонения луча, который стартует от Земли под углом, значительно более близким к зениту (зенит - строго вертикально вверх).
87 - asin(sin(87)/1.0001) = 0.11 градуса29 - asin(sin(29)/1.0001) = 0.0032 градуса0.11 много больше чем 0.0032
Как видно, в первом случае отклонение направления распространения луча от прямолинейного (на картинке отображено синим) значительно больше (на картинке отображена эта особенность, см. зелёные линии). Иными словами, рефракцией, как правило, можно пренебречь в случае околозенитных лучей, а в случае пригоризонтальных рефракцию нужно учитывать, что хорошо известно в рамках наблюдательной астрономии.
Но астрономические объекты находятся вне атмосферы (луч проходит всю толщу атмосферы), поэтому возник следующий вопрос: будет ли рефракция заметно сказываться для наземных объектов, расположенных в нескольких десятках километров от наблюдателя. Для того, чтобы ответить на этот вопрос, мы должны смоделировать распространение луча и проверить моделирование на пригоризонтальных объектах. В качестве последних были использованы несколько высотных объектов Москвы (в скобках указано расстояние до них): главное здание МГУ (30 км), комплекс высоток Москва-Сити (35 км), телевизионная башня Останкинская (44 км).
Математический горизонт
Попытка найти подручными средствами с хорошей точностью математический горизонт (плоскость, перпендикулярная локальной вертикали в точке наблюдения) и сопоставить его с удалёнными наблюдениями не увенчалась успехом, не помогла в том числе попытка применить относительно дешёвый строительный гидроуровень. В результате был приобретён нивелир ADA Basis, с которым дело пошло значительно веселее. В этой модели присутствует компенсатор, который обеспечивает установку зрительной оси нивелира в горизонтальное положение, для чего достаточно выставить прибор лишь примерно горизонтально по пузырьковому уровню.
Чтобы понять, что именно вы видите в окуляр нивелира, приведу одну из фотографий (сделана с помощью смартфона мейзу; данное фото слегка смазано, но суть понять можно):
Горизонтальный отрезок сетки нитей - это математический горизонт, отмеренный нивелиром. Как видно, в данном случае видимый горизонт (видимая граница между лесом и небом) находится ниже математического. Это следствие снижения горизонта из-за расположения наблюдателя (наблюдатель находится выше верхушек деревьев относительно уровня моря).
Два коротких горизонтальных отрезка выше и ниже горизонта - это дальномерный инструмент, который позволяет оценить расстояние до объекта, если известен вертикальный размер h, попавший между отрезками (нитями), для этого надо умножить h на 100; либо наоборот, с помощью этих нитей можно измерить вертикальный размер удалённого объекта между нитями, если известно расстояние L до него, для этого надо поделить L на 100. Поскольку нижняя нить в моих наблюдениях попадала на невидимую часть объектов, я использовал верхнюю нить и горизонт - угловое расстояние между ними в 2 раза меньше, соответственно верхнюю метку я обозначал как "1/200" (то есть расстояние до объекта L я делил на 200, чтобы вычислить высоту объекта между верхней нитью и горизонтальной).
Следует отметить качественную работу компенсатора (в нивелире ADA Basis используется воздушный автоматический компенсатор). Стоит немного пошевелить нивелир, уровень горизонта слегка уплывает, но довольно быстро и без особых переколебаний возвращается на прежнюю позицию. Надо сказать, что некоторые измерения я делал с ошибками, поскольку переоценил скорость компенсации: пока пристраивал смартфон для очередного снимка, мог случайно пошевелить нивелир, и снимок фиксировал горизонт в неверном положении. Впоследствии я учёл эту ошибку, прикрепил смартфон неподвижно, через отдельный держатель, и снимки делал со встроенной задержкой 3 сек. Заодно нужно отметить другую особенность работы с нивелиром - использование механизма для устранения параллакса (подвижности измерительных нитей при смещении глаза/фотоаппарата относительно окуляра).
Абсолютная высота нулевой отметки, использование Google Earth
Для того, чтобы сравнивать относительные высоты всех четырёх объектов (трёх вышеуказанных, плюс моё собственное расположение), мы должны знать высоту их оснований (уровень пола первого этажа) относительно уровня моря. Для этого я искал геодезическую/строительную информацию, рассматривал различные карты высот из сети, думал про использование GPS-навигатора (тестирование встроенного в телефон навигатора дало неприемлемо высокую погрешность определения абсолютной высоты, например на подоконнике я видел высоты от 180 до 260 м). В результате основным источником информации стал Google Earth, который своей основой (насколько я понимаю) имеет карту высот из проекта SRTM. Однако и с ним возникли сложности.
Когда были готовы результаты измерений рефракции, они показали бОльшее искривление луча, чем это выходило из моделирования по параметрам стандартной атмосферы. Первой гипотезой стало наличие в воздухе водяных паров, которые могут вносить дополнительный вклад в рефракцию. Однако измерения показали практически одинаковый результат при давлении водяного пара как 500 Па, так и 1500 Па, то есть при количестве "воды" в атмосфере, отличающемся в три раза. А значит дело было не в водяном паре. Следующей гипотезой стало то, что я неверно определил высоту точки наблюдения относительно моря. Забегая наперёд, эта гипотеза себя оправдала (высота составила 222 м вместо неверно определённых 230 м). Исследование этого вопроса также прояснило нюансы использования Google Earth в качестве источника данных по высоте местности.
Я уже подозревал сам, что в Google Earth представлены некие усреднённые высоты не самой поверхности Земли, а различных поверхностей (крыши домов, верхушки деревьев). А затем нашёл дополнительное подтверждение в следующей работе: "модель SRTM ... измеряет высоту отражающей, а не топографической поверхности: в залесенных районах – высоту деревьев, на заснеженной территории – высоту снежного покрова, а на застроенных территориях – высоту некой осредненной поверхности, которая формируется в процессе обработки радиолокационных сигналов и достаточно неопределенна, так как зависит от большого числа трудноучитываемых факторов, таких, как густота застройки, этажность зданий и т.п. Поэтому, строго говоря, данные SRTM можно рассматривать как цифровую модель рельефа Земли (ЦМР) и выполнять ее корректную оценку точности только на открытых незастроенных территориях, не покрытых кустарниковой и древесной растительностью".
С учётом выделенного текста было решено использовать высоту земель сельхозназначения (далее "поле"), и затем перенести её на точку наблюдения с помощью барометрического альтиметра. В качестве такого альтиметра был использован некий китайский ноунейм прибор (выглядит так) со странным названием "Альтиметр 8 в 1". Изначально доверия к прибору не было, однако он неплохо показал себя при измерении как перепада высот (ездил на лифте с 1 этажа на 12 и обратно), так и перепада абсолютного давления изо дня в день (сравнивал с данными от ближайшей метеостанции, расположенной в паре километров, с учётом того, что изменение давление на 1 мм ртутного столба примерно соответствует перепаду высот 10 метров, поскольку ртуть примерно в 10 тысяч раз плотнее воздуха при нормальных условиях).
Перенос высоты выбранного поля к точке наблюдения осуществлялся следующим образом. Замеряем альтиметром высоту в точке наблюдения, затем в кратчайшее время (чтобы атмосферное давление не успело сильно уплыть) добираемся до выбранного в Google Earth поля, измеряем высоту этого поля и по возвращении вновь измеряем высоту точки наблюдения. За те 30-60 минут, которые длилось путешествие, давление может слегка уплыть, поэтому во-первых двойное измерение (в начале и в конце путешествия) позволяет это усреднить, во-вторых его можно сопоставить с давлениями, которые публикует ближайшая метеостанция.
В итоге была получена высота точки наблюдения примерно 221-223 метра над уровнем моря (будем считать 222 м).
Абсолютная высота наблюдаемых объектов
Два наблюдаемых объекта (МГУ и Останкино) имеют вблизи площадки (без строений и высокой растительности) достаточного размера, чтобы можно напрямую воспользоваться данными Google Earth. Основную сложность по высоте представляли собой башни Москва-Сити. Для них Google Earth выдавал разброс высот от 110 до 130 метров выше уровня моря (Москва-Сити был построен после окончания миссии SRTM). Я взял среднюю величину, 120 м, и она как-то выбивалась из результатов эксперимента. Поэтому были сделаны запросы в пару геодезических фирм, на одном геодезическом форуме, а также на портал градостроительной политики и строительства города Москвы - никаких результатов. Пока я не подобрал наконец правильный запрос в яндекс и наткнулся на порадовавшие меня данные (а именно высота 130 метров вместо 120): "высота башни «Восток» составит 373,7 м, 95 этажей. За относительную отметку 0,00 чистого пола первого этажа принята абсолютная отметка +130,10 м".
Итак, перечислим по порядку абсолютные (выше уровня моря) высотные отметки для всех наших объектов:(0) наблюдательная позиция: 222 м;(1) МГУ: уровень 1 этажа ~ 200 м (это на 6 метров противоречит данным из википедии, там указана высота основания 194 м, но источник я полагаю ненадёжным);(2) Москва-Сити: основное (самое высокое) здание - вышеупомянутая башня Федерация-Восток, уровень 1 этажа 130 м;(3) Останкинская башня: уровень основания ~ 160 м.
Результаты измерений
Здесь представлены фотографии наилучшего качества по изображению (например, первая фотография выбрана как единственная, где просматривается форма звезды в верхушке шпиля МГУ). Что касается измерений, некоторые из этих фотографий затем уточнялись благодаря более стабильному закреплению смартфона. Также отметим неэстетичный анахронизм на переднем плане - различные городские провода непонятного назначения, среди которых иной раз приходится искать нивелирную нить горизонта.
(1) МГУ, 30 км:
Зная высоты характерных точек здания/шпиля (на картинке приведены две из них, 235 и 172 метра) относительно пола первого этажа, а также зная расстояние до объекта (30 км), мы можем поделить последнее на 200 и получить 150 м - это вертикальное расстояние между нитями "Горизонт" и "1/200" на расстоянии 35 км. Далее остаётся соотнести любую из меток (например 235 метров) с её пиксельной координатой и вычислить высоту, которую отсекает математический горизонт наблюдателя на здании МГУ. Наиболее качественное измерение дало величину 78 метров. Над уровнем моря 78+200 = 278 м. За вычетом высоты наблюдателя 278-222 = 56 м.
Схематичная вставка справа приведена, чтобы примерно представить, насколько ниже математического горизонта расположено основание здания МГУ.
Тот факт, что мы видим часть здания МГУ ниже математического горизонта (в районе жёлтой надписи "Горизонт"), говорит о том, что рельеф местности от точки наблюдения до МГУ снижен (его высота относительно уровня моря ниже, чем высота точки наблюдения 222 м).
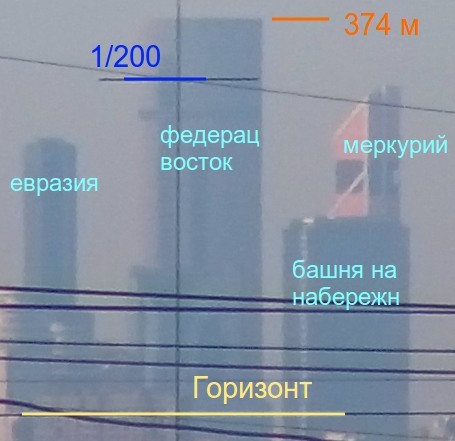
(2) Москва-Сити, 35 км:
(здесь - эта же фотография в более широкой панораме)
На рисунке отмечена высота (374 м) самой высокой башни - Федерация-Восток. Высоты остальных башен можно посмотреть здесь.
Пиксельные измерения в этом случае дали уровень высоты, отсекаемый горизонтом наблюдателя, 168 м. Над уровнем моря 168+130 = 298 м. Относительно высоты наблюдателя 298-222 = 76 м.
(3) Останкинская башня, 44 км:
Вставка справа схематично показывает, насколько ниже математического горизонта расположено основание башни, а также обозначает высоты некоторых точек объекта выше основания.
Отсекаемая горизонтом высота составила 186 м. Над уровнем моря 186+160 = 346 м. Относительно высоты наблюдателя 346-222 = 124 м.
Расчёт атмосферной рефракции
При численном моделировании рефракции использовались данные из ГОСТ 4401-81 ("Атмосфера стандартная, параметры", дата введения - июль 1982), разбивка атмосферы на слои по высоте и закон Снеллиуса при переходе в следующий слой. Методика расчёта позволила оценить, на какой высоте (относительно высоты наблюдателя) будет проходить луч света, пущенный под заданным углом (в том числе горизонтально), на заданном расстоянии от источника (в случае наших объектов эти расстояния равны 30, 35 и 44 км).
Полученные результаты можно подбить в следующую таблицу:
где L - расстояние до объекта наблюдения, км;"измерение" - измеренная высота отсечки математическим (локальным) горизонтом наблюдателя, относительно высоты самого наблюдателя, м; "вакуум" - высота отсечки для случая планеты радиусом 6371км и отсутствия рефракции (вакуум или однородная по высоте атмосфера), м;"ГОСТ" - высота отсечки для случая численного расчёта по стандартной атмосфере (ГОСТ 4401-81), м;"разница" - насколько не сошлись "измерение" и расчёт "ГОСТ".
Заключение
В целом измерения показывают неплохое совпадение с расчётом: 2-4 метра на расстояниях от 30 до 44 км (на фоне погрешности измерений около 0.5-0.7 м на пиксель).
Атмосферная рефракция, несмотря на малый перепад высот между наблюдателем и наблюдаемым объектом, заметно влияет на высоту башен над горизонтом. Без атмосферы они бы выглядели несколько ниже (глубже под горизонтом), а рефракция их как бы приподнимает, "вытаскивает" из-за горизонта. Покажем этот эффект на примере Останкинской башни (44 км):
(справа для иллюстрации приведена фотография башни из интернета)
На рисунке обозначены следующие высоты:* 62м - разница высоты наблюдателя 222 м и основания башни 160 м над уровнем моря, которая отсекалась бы математическим горизонтом наблюдателя в случае плоской земли и без атмосферы;* 62+152 = 214м - высота отсечки для сферичной Земли в отсутствие атмосферы;* 62+126 = 188м - ожидаемая высота отсечки для сферичной Земли с учётом рефракции;* 62+124 = 186м - измеренная высота отсечки.Как видно, измеренная высота отсечки 186м с хорошей точностью совпала с расчётной 188м (особенно если вспомнить про все погрешности, которые суммарно, видимо, превысят эти два метра).
Башня, расположенная на расстоянии 44 км, из-за рефракции оптически приподнимается атмосферой на 214-188 = 26 метров. Величина небольшая, но заметная (подписано на рисунке).
Примечание 1. Перепадом высот геоида между указанными точками в рамках описанного эксперимента можно пренебречь, по оценкам этого сервиса он составляет всего 0.2 метра. Поэтому на этом участке эквипотенциальную поверхность мы считаем участком сферы.
Примечание 2. Тема пригоризонтальных наблюдений в последние годы постоянно поднимается в плоскоземельных баталиях, в духе "ага, мы посмотрели, и гора/здание, которая должна была исчезнуть за горизонтом, не исчезла". На это я всегда акцентировал, что первейшие наблюдения должны проводиться с астрономическими объектами вблизи зенита, а уж потом можно приступать к наблюдениям в сторону горизонта, поскольку они сложнее, и требуют более тщательного рассмотрения из-за неизвестной величины рефракции. Так и вышло в рамках описанного эксперимента - в целом его поставить удалось, однако всё это потребовало времени, чтобы увязать полученные результаты и добыть недостающие данные.






Наука | Научпоп
9.5K постов83K подписчика
Правила сообщества
Основные условия публикации
- Посты должны иметь отношение к науке, актуальным открытиям или жизни научного сообщества и содержать ссылки на авторитетный источник.
- Посты должны по возможности избегать кликбейта и броских фраз, вводящих в заблуждение.
- Научные статьи должны сопровождаться описанием исследования, доступным на популярном уровне. Слишком профессиональный материал может быть отклонён.
- Видеоматериалы должны иметь описание.
- Названия должны отражать суть исследования.
- Если пост содержит материал, оригинал которого написан или снят на иностранном языке, русская версия должна содержать все основные положения.
- Посты-ответы также должны самостоятельно (без привязки к оригинальному посту) удовлетворять всем вышеперечисленным условиям.
Не принимаются к публикации
- Точные или урезанные копии журнальных и газетных статей. Посты о последних достижениях науки должны содержать ваш разъясняющий комментарий или представлять обзоры нескольких статей.
- Юмористические посты, представляющие также точные и урезанные копии из популярных источников, цитаты сборников. Научный юмор приветствуется, но должен публиковаться большими порциями, а не набивать рейтинг единичными цитатами огромного сборника.
- Посты с вопросами околонаучного, но базового уровня, просьбы о помощи в решении задач и проведении исследований отправляются в общую ленту. По возможности модерация сообщества даст свой ответ.
Наказывается баном
- Оскорбления, выраженные лично пользователю или категории пользователей.
- Попытки использовать сообщество для рекламы.
- Фальсификация фактов.
- Многократные попытки публикации материалов, не удовлетворяющих правилам.
- Троллинг, флейм.
- Нарушение правил сайта в целом.
Окончательное решение по соответствию поста или комментария правилам принимается модерацией сообщества. Просьбы о разбане и жалобы на модерацию принимает администратор сообщества. Жалобы на администратора принимает и общество Пикабу.