7. Что такое триангуляция. Геодезия и отвага
Это часть лонгрида об истории Французской Геодезической Миссии в Перу. Предыдущие части можно найти тут:
1. О форме Земли: тыква или Дыня.
2. О том, что такое градусные измерения. Как определить размеры Земли.
6. Как готовились к экспедиции ч.1.
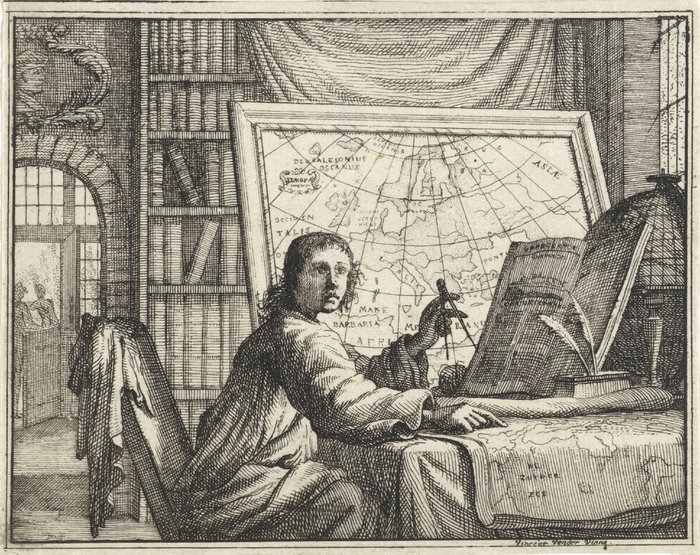
О трудных буднях картографов. (Man met passer bij landkaarten, Vincent Laurensz. van der Vinne, https://www.rijksmuseum.nl/)
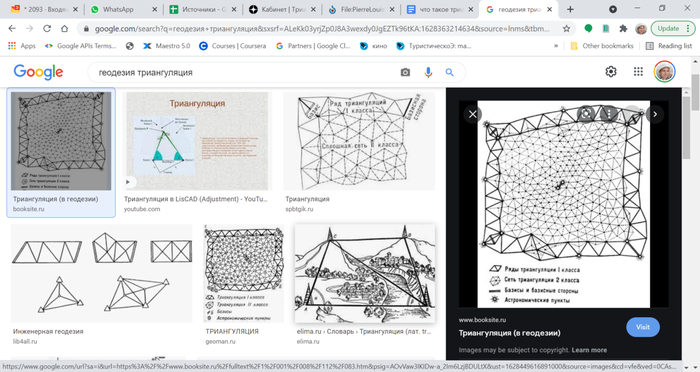
Триангуляция, как следует из названия, связана с треугольниками, а точнее - их углами (и одной стороной). В геодезии этот метод определения расстояний и/или координат использовался как основной вплоть до конца XX века. Так что, если вбить это слово в поисковик, то мы увидим что-то такое:
Это сеть триангуляции в геодезическом понимании. Но кроме геодезии (где она порядком устарела), сегодня триангуляция применяется для построения поверхностей по облаку точек.
То есть, чтобы на компьютере (для игры, спецэффектов в фильме и любых других вещей) получить поверхность - нужно ее построить. Поскольку поверхность не обязательно будет являться ровной (плоскостью), все ее изгибы можно передать при помощи треугольников (чем больше треугольников, тем более реалистично и сглажено будет выглядеть поверхность). Примерно так:
Как триангуляция появилась в геодезии?
Был такой голландский ученый, живший в XVI веке, Эратосфен Батавский (в те времена было принято брать себе хвастливые прозвища, подражая ученым древности), он же Виллеборд Снелл. Именно он использовал и популяризировал известную из математики триангуляцию для геодезических работ.
Портрет землемера (во времена и в местах Снелла), аноним, 1650 - 1674 (https://www.rijksmuseum.nl/)
Подобно Эратосфену, Снелл тоже выполнял градусные измерения для определения радиуса Земли. Ему тоже нужно было найти длину дуги меридиана в градусах и в линейной мере (милях, к примеру). Однако караванов с погонщиками в северной Европе не было, так что расстояние пришлось определять самостоятельно.
Как устроена триангуляция?
Предположим, мы хотим найти расстояние между весьма удаленными точками (допустим удаленных на 100 километров). Просто измерить это расстояние невозможно: нет прямой видимости, нет возможности хотя бы построить прямую линию между точками (ведь одна может находиться на холме а другая на низменности, между ними могут быть реки, овраги и озера.
На помощь приходит цепочка треугольников.
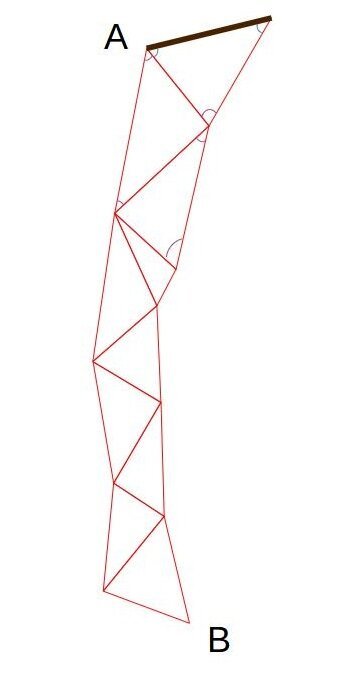
Это звено триангуляции АВ
Допустим, нам нужно найти расстояние (АВ). Мы строим цепочку стыкующихся треугольников вокруг этой линии и измеряем небольшую (до 10 км) сторону треугольника A-1.
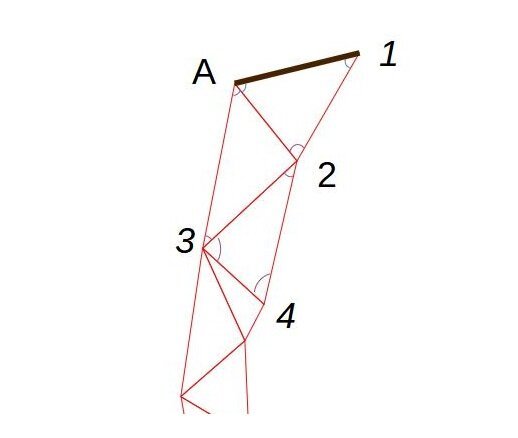
Фрагмент триангуляции. А-1 - измеренная сторона (базис).
Она на рисунке помечена коричневым. Также мы угломерным прибором (квадрантом, астролябией, тахеометром, что есть) измеряем все внутренние углы треугольника 1-А-2. Получается, нам известны одна сторона и углы в треугольнике. Значит мы можем вычислить оставшиеся стороны в треугольнике. Среди прочего - мы найдем сторону А-2. И, если мы измерим все углы в треугольнике А-2-3, то сможем найти все стороны и для него тоже. Таким образом, последовательно решая стыкующиеся треугольники, для которых известны внутренние углы, мы сможем отыскать длины сторон всех треугольников.
Тут возникает нестыковка: мы можем отыскать все элементы треугольника по стороне и всего лишь двум углам. Значит, измерять все углы нет необходимости, достаточно измерить только два из трех! Теоретически это так. Однако на практике измеряют третий угол, чтобы обеспечить избыточность измерений. Как минимум - это такой простейший контроль: если сумма всех углов не будет равна 180 градусам - где-то в измерения вкралась серьезная ошибка.
На практике существует целая теория уравнительных вычислений (курс ТМОГИ студенты проходят не один и не два семестра, и выдерживают его лишь самые сосредоточенные), которая позволяет оценить погрешность, с которой были выполнены измерения и вычисления окончательной величины (расстояния), но в первой трети XVIII века, о которой я рассказываю, про все это имелись скорее смутные догадки.
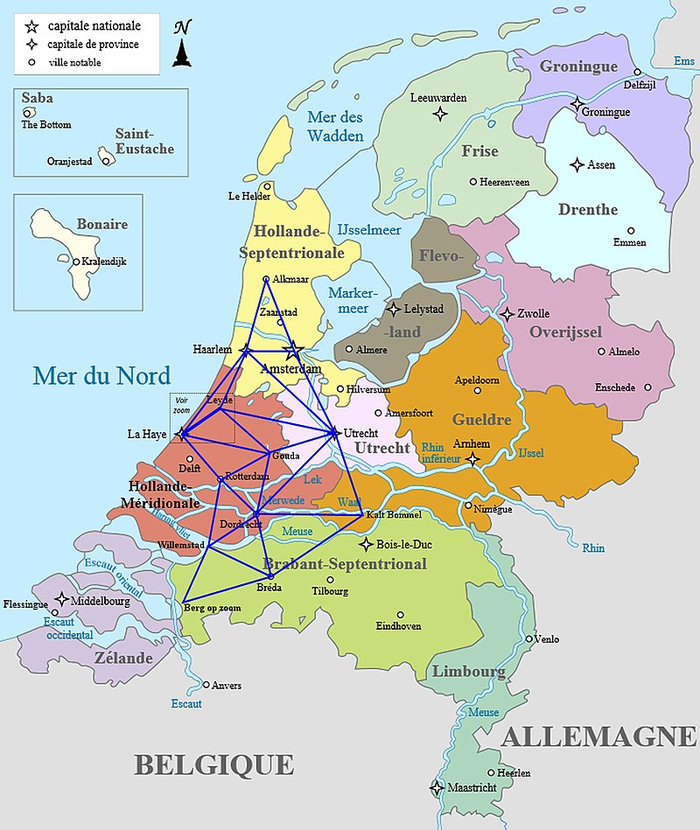
Примерно по такой схеме, как описана выше, строил свои рассуждения Снелл. Он измерил расстояние от своего дома до шпиля местной церкви, а затем построил цепочку стыкующихся треугольников (триангуляции), которая позволила ему определить расстояние между городами Алкмар и Берген-оп-Зом, которые лежат на одном меридиане. Далее, зная длину дуги меридиана в линейной мере (милях) и в градусной мере - он мог вычислить радиус Земли, подобно Эратосфену (настоящему Эратосфену, Киренскому).
Триангуляция Снелла, 1621 г. (картинка из Вики-статьи про Снеллиуса (https://upload.wikimedia.org/wikipedia/commons/b/bd/Triangul...)
Метод Снелла оказался удачным, выполнимым и был взят на вооружение. Разумеется, по мере применения он совершенствовался: измерения выйдут точнее, если треугольники будут, по возможности, равносторонние или хотя бы равнобедренные. Придумали также делать дополнительный базис (измерять еще одну сторону треугольника где-то в конце цепочки) - для контроля. Эта сторона треугольника будет известна из измерений и из вычислений. Разница поможет оценить погрешность, с которой проводились работы.
Кстати, триангуляция была основным методом высокоточных геодезических измерений до самого конца XX века, пока не появились спутниковые системы позиционирования, GPS/ГЛОНАСС. Но это уже - совсем другая история.
Современный (конец ХХ века) пункт триангуляции в Тульской области.
А мы вернемся на рубеж XVII - XVIII веков. Чуть позже, чем Снелл, триангуляцию для определения длину дуги парижского меридиана использовал Джованни Кассини - директор Парижской обсерватории. А потом его сын - Жак Кассини. Именно из результатов наблюдений семьи Кассини стало ясно, что длина 1 градуса меридиана неодинаковая на разных широтах. И эти результаты градусных измерений подливали масла в огонь спора ньютонианцев и декартистов.
Зачем была нужна триангуляция в Экваториальной Градусной Экспедиции?
Вернемся к Экваториальной экспедиции 1735 года. Что именно предстояло сделать ученым?
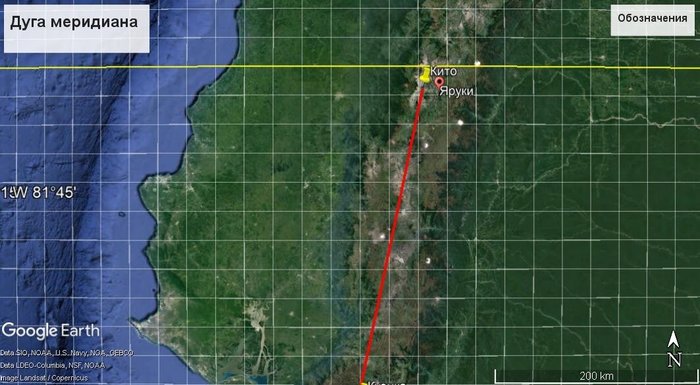
Есть кусочек дуги меридиана, который начинается где-то в районе экватора. И его длину необходимо измерить. Это примерно между Кито и Куэнкой (городами в современном Эквадоре).
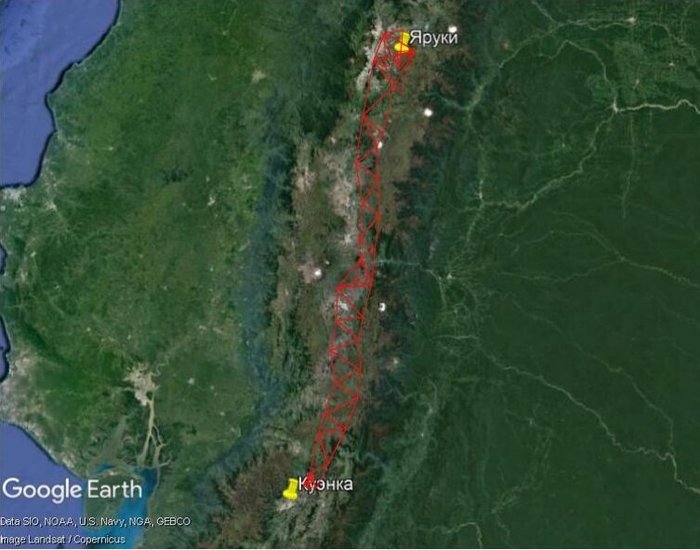
Ученые решают разбить вдоль меридиана (с севера на юг) цепочку треугольников. Треугольники требуется делать по возможности равносторонними или хотя бы равнобедренными, на местности необходимо обеспечить видимость хотя бы на две соседние вершины. Учитывая расстояния и сложности местного рельефа, треугольников становится более сорока (сорок семь, если точнее).
На современную карту тут наложены треугольники перуанской экспедиции (примерный экскиз)
Измерена будет сторона одного из северных треугольников (базис в районе Яркуи) и еще одна сторона на юге (базис в Куэнке), для контроля результатов. К сожалению, ввиду того, что это горная цепь с ущельями, скалами, реками и провалами, удобное плато для базиса было найти трудно, поэтому его длина существенно меньше (раза в четыре), чем длины сторон основных треугольников. Базис составит около 12 км. Во всех прочих (47) треугольниках будут измерены внутренние углы. После этого ученые последовательно вычислят длины сторон всех треугольников.
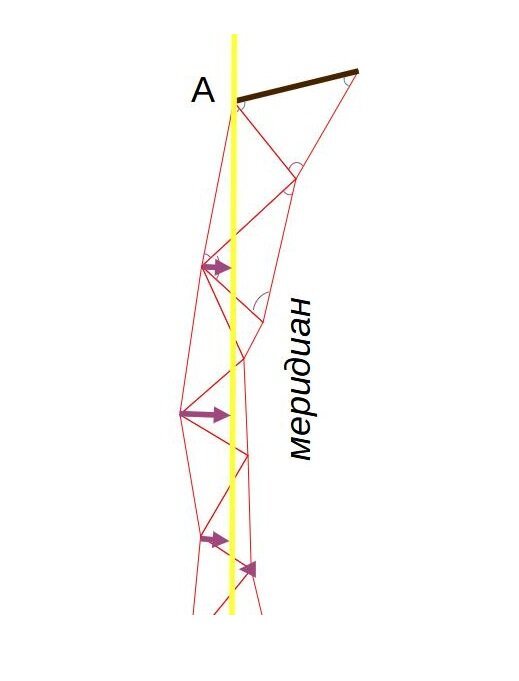
Казалось бы: как теперь из наклонных сторон треугольников получить длину меридиана? Ученые будут вычислять длину проекции каждой западной стороны треугольника на меридиан. В сумме они дадут длину дуги меридиана:
Длину дуги меридиана вычисляли по сумме проекций сторон треугольника на меридиан
Эта задача, хотя и должна была быть выполнена с наибольшей точностью в тяжелейших условиях тропического климата и высоких гор - все же была чисто геометрической. И господа Буге, Лакондамин и Годен с оптимизмом смотрели в будущее. Но для самых точных в истории измерений им требовались самые точные инструменты. Этим и занялся Луи Годен в Гринвиче.




Наука | Научпоп
9.3K поста82.8K подписчиков
Правила сообщества
Основные условия публикации
- Посты должны иметь отношение к науке, актуальным открытиям или жизни научного сообщества и содержать ссылки на авторитетный источник.
- Посты должны по возможности избегать кликбейта и броских фраз, вводящих в заблуждение.
- Научные статьи должны сопровождаться описанием исследования, доступным на популярном уровне. Слишком профессиональный материал может быть отклонён.
- Видеоматериалы должны иметь описание.
- Названия должны отражать суть исследования.
- Если пост содержит материал, оригинал которого написан или снят на иностранном языке, русская версия должна содержать все основные положения.
- Посты-ответы также должны самостоятельно (без привязки к оригинальному посту) удовлетворять всем вышеперечисленным условиям.
Не принимаются к публикации
- Точные или урезанные копии журнальных и газетных статей. Посты о последних достижениях науки должны содержать ваш разъясняющий комментарий или представлять обзоры нескольких статей.
- Юмористические посты, представляющие также точные и урезанные копии из популярных источников, цитаты сборников. Научный юмор приветствуется, но должен публиковаться большими порциями, а не набивать рейтинг единичными цитатами огромного сборника.
- Посты с вопросами околонаучного, но базового уровня, просьбы о помощи в решении задач и проведении исследований отправляются в общую ленту. По возможности модерация сообщества даст свой ответ.
Наказывается баном
- Оскорбления, выраженные лично пользователю или категории пользователей.
- Попытки использовать сообщество для рекламы.
- Фальсификация фактов.
- Многократные попытки публикации материалов, не удовлетворяющих правилам.
- Троллинг, флейм.
- Нарушение правил сайта в целом.
Окончательное решение по соответствию поста или комментария правилам принимается модерацией сообщества. Просьбы о разбане и жалобы на модерацию принимает администратор сообщества. Жалобы на администратора принимает и общество Пикабу.