Зачем нужна математика в компьютерных играх? [часть 1]
Привет-привет.
Почти 200 дней назад я написал комментарий под одним из постов, в котором немножко популярно объяснил, зачем в компьютерных играх (и компьютерной графике вообще) нужна линейная алгебра. Тот самый линал, что любой студент-технарь изучает на 1 курсе универа.
О том, что пост мне пилить лень, я предупредил сразу, но пикабушников это не убедило, у меня прибавилось over 100 подписчиков (с одного коммента-то!), так что почему бы и нет.
Примечание: рассказывать я буду с расчётом на людей, понимающих, что такое матрица, вектор и cross product, но, несмотря на это, постараюсь всё объяснить и расписать понятно даже для гуманитария (в идеале, линал для понимания поста изучать не нужно).
Как говорил Стивен Хокинг, «Любая формула уменьшает количество моих читателей вдвое». Пока, ребят).
Чуть-чуть школьной геометрии. Что такое вектор? Это стрелка. У неё есть длина и направление. Есть двумерные векторы (у которых направление — от 0 до 360 градусов), есть трёхмерные (у них есть два направления, оба от 0 до 360).
В абстрактной алгебре есть даже бесконечномерные векторы, но это нам не нужно)
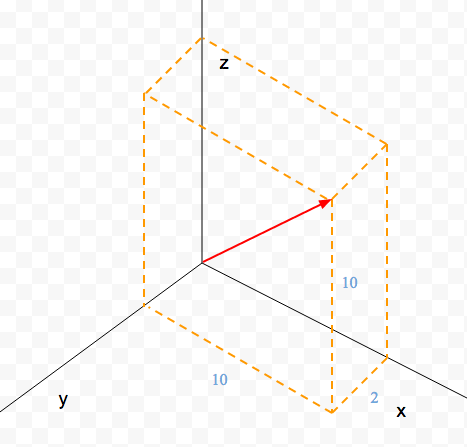
Вот эта красная стрелка — и есть вектор. Линии, обозначенные буквами x, y, z, — называются умным словом координатные прямые.
Давайте запихнём наш вектор в коробку (оранжевые пунктирные прямые) и померяем её длину, ширину и высоту. Эти значения называются координатами вектора. В частности, здесь это (10, 2, 10). [именно в таком порядке, (x, y, z)]
Теперь если мы кому-нибудь скажем «вектор (10, 2, 10)», он сразу сможет его нарисовать, и это окажется в точности тот же вектор.
В школе на геометрии обычно изучают скалярное произведение двух векторов. Вот оно:
А ещё его изучают в универе, на линейной алгебре.
А теперь главное: применение! Давайте представим, что мы хотим нарисовать на экране 3D-модель. Любая 3D-модель состоит из треугольников, и, в общем, нарисовать кучу треугольников рандомным цветом — достаточно лёгкая задача.
Не слишком привлекательно, да? Давайте попробуем сделать нормальные тени.
Нужно узнать, каким цветом заливать каждый треугольник.
Итак, для начала введём вектор, который начинается в центре модели, а заканчивается там, где и будет источник освещения. А именно — вектор (0, 0, 1).
Так получается потому что ось z направлена на нас, а координаты — что-то вроде процентов, например, точка (0, 0, 0.5) — это точка ровно посередине между центром модели (которая, как мы считаем, находится «позади экрана») и экраном компьютера :)
А теперь давайте проведём из каждого треугольника перпендикулярный ему вектор (причём длины 1) и скалярно перемножим с нашим вектором источника освещения.
Это и будет коэффициент освещённости треугольника:
— если 0, то совсем не освещён, рисуем чёрным.
— если 0.5, то освещён наполовину, рисуем серым 50%.
— если 1, то полностью освещён, рисуем белым.
— и тому подобное.
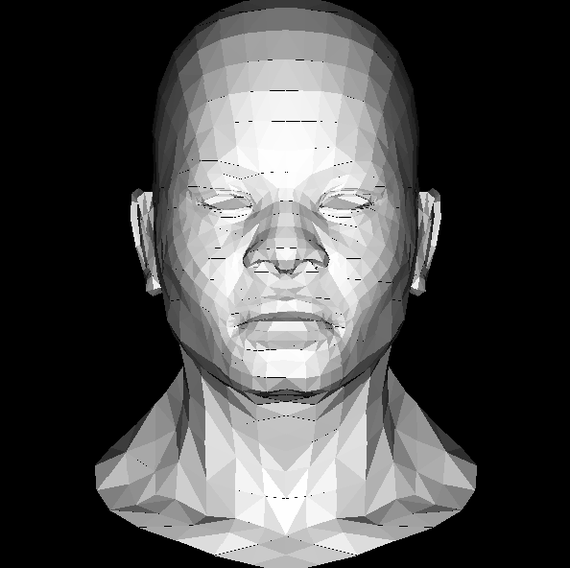
И наша модель обретает жизнь!
Есть и более продвинутые модели освещения (например, Фонга), про них, возможно, напишу в будущем, но вряд ли.
И небольшое примечание про перпендикулярные векторы.
Перпендикуляр треугольника находится с помощью векторного произведения: берём любые 3 точки треугольника и составляем из них 2 вектора. Векторное умножение выглядит так:
Как видно, скалярное произведение — число, а векторное произведение — вектор.
Нужно ещё сделать, чтобы перпендикуляр был длиной 1, а это операция нормирования вектора:
С кодом модели можно поиграться тут: http://jsfiddle.net/2wvyga24/24/ .
Также можно почитать статьи хабраюзера haqreu: https://habrahabr.ru/post/248153/ .
Матрицы — это главная причина, по которой всё, что в играх должно вращаться или двигаться, вращается или двигается. И это именно то, как работает Free Transform в фотошопе.
Матрица — это обычная табличка с числами. Их даже можно складывать и умножать.
Если сложение — достаточно очевидная вещь, то вот умножение...
Запоминается простым правилом «строка на столбец». Берём 2 строку первой матрицы и скалярно умножаем на 1 столбец второй. Это и будет элемент, стоящий во 2 строке 1 столбца произведения.
Казалось бы, зачем так усложнять? Почему не умножать обычным образом?
Разгадка проста: изначально матрицы были придуманы, чтобы решать уравнения. Но это мы не будем затрагивать...
Ведь вдруг оказалось, что матричное умножение — это то, что делает матрицы столь полезными для компьютерной графики!
А ещё можно матрицы умножать на векторы. По обычному правилу: по сути, вектор — и есть матрица, просто с одним столбцом (или одной строкой, но это совсем отдельная тема).
Давайте возьмём плоскость и засунем любую картинку в нулевые координаты (т.е. левый нижний угол квадратика с кексом имеет координаты 0,0).
Как её теперь повернуть на 45 градусов? Картинка ведь состоит из точек (пикселей), и нужно найти новые координаты для каждой точки. Нужна какая-нибудь формула.
И она есть!
Итак, любая точка с координатами (x, y) — по сути, вектор с координатами (x, y) же. Умножение на матрицу 2×2 — это преобразования пространства (сжатие, поворот и тому подобное).
И поворот выглядит вот так:
Координаты x', y' — это и есть новые координаты после поворота.
А вот масштабирование (увеличение / уменьшение) — на λ по x и на η по y.
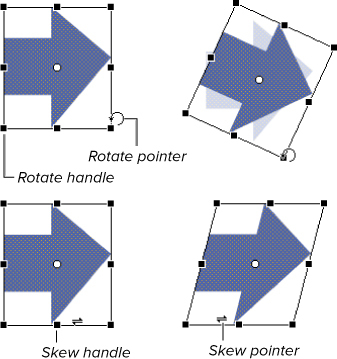
И наконец, «cкос», также известный как Skew / Shear. Фотошоперы поймут).
Поскольку ничего не понятно, вот утащенная из интернета картинка:
Например, мы повернули картинку на 30 градусов, а затем увеличили в 3 раза по вертикали и в 2 по горизонтали.
Тогда пиксель с координатами (50,30) перейдёт в пиксель с координатами (2, 175):
Я же ничего не перепутал, да?
Все наши преобразования происходят вокруг начала координат — точки (0, 0). Если мы хотим повернуть картинку вокруг центра, нужно вставлять её так, чтобы центр картинки оказался в точке (0, 0).
Увы, перемещения с помощью матрицы выразить нельзя. Так что был придуман небольшой хак: давайте перейдём к матрицам и векторам 3×3:
Все предыдущие преобразования остаются в силе:
Но теперь мы можем выразить перемещения!
Ну что ж, теперь несколько хороших моментов:
— Умножение матриц не перестановочно, т.е. обычно A × B ≠ B × A. От перестановки множителей меняется произведение. Например, [переместить на x,y и повернуть на φ] — не то же самое, что [повернуть на φ и переместить на x,y].
— Однако ассоциативно, т.е. (A × B) × C = A × (B × C).
— А значит, перемножение матриц даёт суммарное преобразование. Например: A — поворот, B — перенос, C — масштаб. Тогда матрица A × B × C — это всё сразу. И произведение матрицы (A × B × C) на вектор — это преобразование вектора всеми тремя способами на все те же координаты.
— Обратная матрица — обратное преобразование. Например, поворот на 30 градусов — поворот на -30. Увеличение вдвое — увеличение в 0.5.
И самое важное:
— Всё это переносится практически без изменений в трёхмерное пространство. Векторы и матрицы становятся четырёхмерными (чтобы выражать перемещения), появляется несколько видов поворотов... ну и всё.
P. S. вероятно, следующие посты не будут публиковаться в сообщество.
P. P. S. поскольку мне лень, ждать продолжения бывает долго х)
Вопросы в комментарии :D


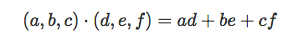

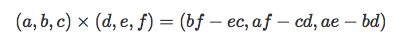
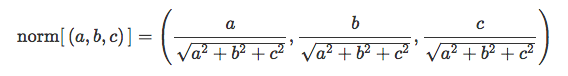

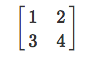
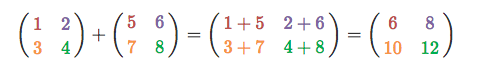

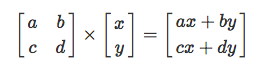


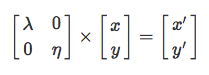
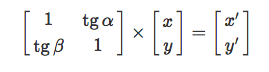
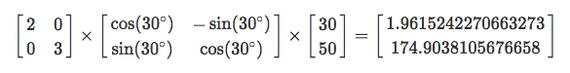
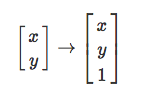
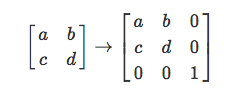
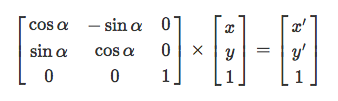
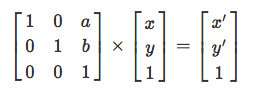
Лига Разработчиков Видеоигр
8.6K поста23.1K подписчиков
Правила сообщества
ОБЩИЕ ПРАВИЛА:
- Уважайте чужой труд и используйте конструктивную критику
- Не занимайтесь саморекламой, пишите качественные и интересные посты
- Никакой политики
СТОИТ ПУБЛИКОВАТЬ:
- Посты о Вашей игре с историей её разработки и описанием полученного опыта
- Обучающие материалы, туториалы
- Интервью с опытными разработчиками
- Анонсы бесплатных мероприятий для разработчиков и истории их посещения;
- Ваши работы, если Вы художник/композитор и хотите поделиться ими на безвозмездной основе
НЕ СТОИТ ПУБЛИКОВАТЬ:
- Посты, содержащие только вопрос или просьбу помочь
- Посты, содержащие только идею игры
- Посты, единственная цель которых - набор команды для разработки игры
- Посты, не относящиеся к тематике сообщества
Подобные посты по решению администрации могут быть перемещены из сообщества в общую ленту.
ЗАПРЕЩЕНО:
- Публиковать бессодержательные посты с рекламой Вашего проекта (см. следующий пункт), а также все прочие посты, содержащие рекламу/рекламные интеграции
- Выдавать чужой труд за свой
Подобные посты будут перемещены из сообщества в общую ленту, а их авторы по решению администрации могут быть внесены в игнор-лист сообщества.
О РАЗМЕЩЕНИИ ССЫЛОК:
Ссылка на сторонний ресурс, связанный с игрой, допускается только при следующих условиях:
- Пост должен быть содержательным и интересным для пользователей, нести пользу для сообщества
- Ссылка должна размещаться непосредственно в начале или конце поста и только один раз
- Cсылка размещается в формате: "Страница игры в Steam: URL"