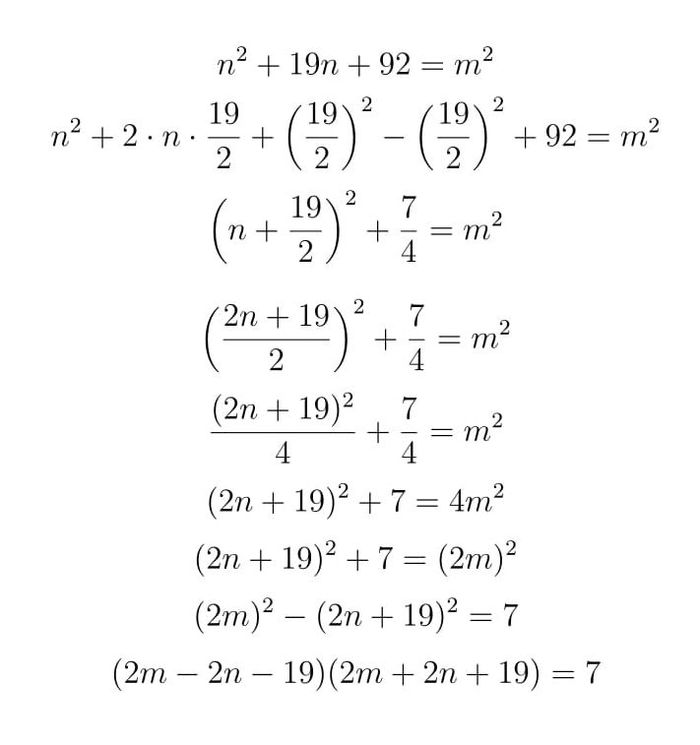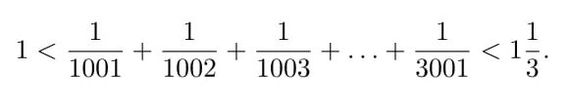Поступаем в универ нахалявую. Некоторые олимпиадные задачи
Всем доброго времени суток. Вот и начался учебный год, а значит скоро начнутся олимпиады с помощью которых можно автоматом получить 100 балов на ЕГЭ и забыть про него как страшный сон.
Хочу рассказать как решаются некоторые, наиболее часто встречающиеся, задачи олимпиадной математики. Для примера возьму региональную олимпиаду RMO–1992
Задача на теории чисел и основную теорему арифметики:
Когда видишь квадратный двучлен первое, что надо делать это попытаться привести его к более простому виду. И самый простой способ сделать это - выделить полный квадрат, давайте так и сделаем, следуя стандартной процедуре получим:
Тут чтобы избавиться от лишних дробных чисел мы вынуждены били умножить все на 4, и заметить, что 4 есть 2 в квадрате. На самом деле задача почти решена, давайте заметим что число 7 - простое, то есть ее делителями могут быть только числа 1 и 7. А в правой части как-раз стоит произведение двух целых чисел. Значит возможны только два варианта:
Вот мы и решили задачу!!! Ответ: n = -8 или n = -11
В данной задаче нам очень повезло, что после разложения на множители в правой части оказалось простое число, а что делать если это не так? Попробуйте сами догадаться использовав лишь основную теорему арифметики которая звучит так:
Любое целое число можно однозначно, с точность до перестановки множителей и умножения на 1 и -1 разложить в произведение простых чисел.
И решите аналогичную задачу для двучлена: n^2 +13n +67, проделав те-же самые рассуждения.
В следующем посте (если зайдет) будет еще одна задача, часто встречающаяся в олимпиадах - оценка суммы. Мы докажем следующий факт: