Полиномиальное и экспоненциальное время выполнения алгоритма. В чем разница⁠⁠

Полиномиальное время

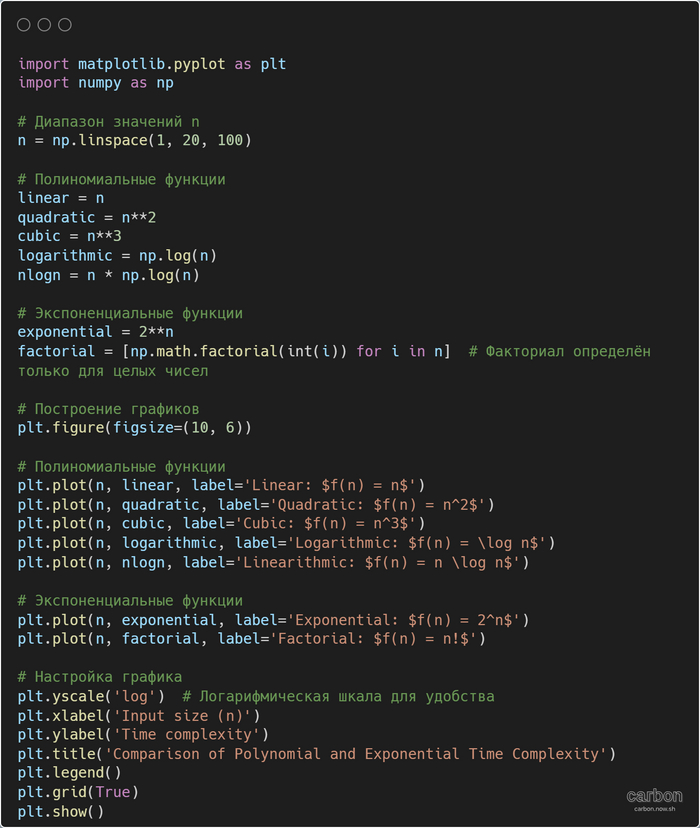
• Полиномиальное время —время выполнения алгоритма, которое растёт как полином (многочлен) от размера входных данных. Если время выполнения алгоритма можно выразить как (O(n^k)), где (n) — размер входных данных, а (k) — константа, то такой алгоритм работает за полиномиальное время.

  Примеры:

  1. Сортировка списка: Алгоритмы, такие как сортировка слиянием или быстрая сортировка, работают за (O(n \log n)), что является полиномиальным временем.

  2. Поиск кратчайшего пути в графе: Алгоритм Дейкстры работает за (O(n^2)) или (O(n \log n)) в зависимости от реализации, что также полиномиально.

  Особенности:

  • Алгоритмы, работающие за полиномиальное время, считаются эффективными и практически применимыми.

  • Задачи, которые можно решить за полиномиальное время, относятся к классу P.

  Экспоненциальное время

  Экспоненциальное время — время выполнения алгоритма, которое растёт экспоненциально в зависимости от размера входных данных. Если время выполнения можно выразить как (O(k^n)), где (n) — размер входных данных, а (k) — константа, то такой алгоритм работает за экспоненциальное время.

  Примеры:

  1. Задача коммивояжёра: Решение методом полного перебора всех возможных маршрутов требует (O(n!)) времени, что хуже экспоненциального.

  2. Перебор всех подмножеств: Алгоритм, который проверяет все возможные подмножества множества из (n) элементов, работает за (O(2^n)).

  Особенности:

  • Алгоритмы, работающие за экспоненциальное время, считаются неэффективными для больших входных данных, так как время выполнения становится непрактично большим даже при относительно небольших (n).

  • Задачи, которые могут быть решены только за экспоненциальное время, часто относятся к классам NP-трудных или NP-полных.

1. Полиномиальное время:

   • Алгоритмы, работающие за полиномиальное время, считаются практически применимыми, так как они могут обрабатывать большие объёмы данных за разумное время.

   • Задачи класса P (решаемые за полиномиальное время) являются основой для многих приложений в компьютерных науках, таких как обработка данных, сети, криптография и искусственный интеллект.

1. Экспоненциальное время:

   • Алгоритмы, работающие за экспоненциальное время, становятся непрактичными даже для относительно небольших входных данных. Например, при (n = 100), (2^n) уже превышает количество атомов в наблюдаемой Вселенной.

   • Задачи, которые могут быть решены только за экспоненциальное время, часто требуют использования приближённых методов, эвристик или параллельных вычислений.

Пример для понимания

Задача её для (n = 10) и (n = 100):

• Полиномиальное время ((n^2)):

  • При (n = 10): (10^2 = 100) операций.

  • При (n = 100): (100^2 = 10,000) операций.

• Экспоненциальное время ((2^n)):

  • При (n = 10): (2^{10} = 1,024) операций.

  • При (n = 100): (2^{100} \approx 1.26 \times 10^{30}) операций.

При (n = 100) полиномиальный алгоритм выполнит 10 000 операций, что вполне реально, а экспоненциальный алгоритм потребует (1.26 \times 10^{30}) операций, что практически невозможно.

GIT