Парадокс Сена
Всем привет! Я продолжаю свою серию постов по популяризации науки :) Пока я выкладываю материалы по теории игр.
Штрафы за отклонение от стратегий
Введя штрафы за какие-то поступки, можно достаточно сильно поменять матрицу платежей.
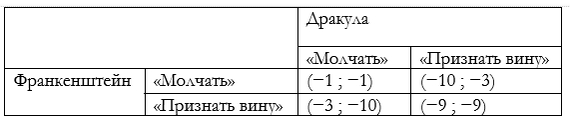
Пусть Франкенштейн и Дракула заключили предварительно такой договор: в случае, если кто-то один из них попытается заложить другого, друзья того, кого он заложил, поймают и посадят его в подвал на 3 года. Посмотрим, как изменится матрица платежей в данном случае.
Ну что же, очевидно, что теперь уже взаимное молчание является равновесием. Так что да, такой механизм вполне работает.
Парадокс Сена
Я закончу первоначальное знакомство с теорией игр и концепцией равновесий по Нэшу и Парето-оптимальности еще одним парадоксом, связанным с концепцией оптимума в смысле Парето.
Либеральный парадокс, также называемый парадоксом Сена, представляет собой логический парадокс, предложенный Амартия Сеном в статье 1970 года. Он показывает, что ни одна социальная система не может одновременно быть привязанной к минимуму свободы, и приводить к эффективности по Парето.
Этот парадокс спорен, потому что он, кажется противоречащим классическому либеральному утверждению, что рынки одновременно эффективны и уважают личные свободы.
В исходном примере Сена использовалось простое общество, в котором было всего два человека и одна социальная проблема для рассмотрения. Назовем этих двух членов общества «Гарри Гудини» и «Дэвид Копперфильд». В этом обществе существует только одна копия «Теории игр». Эту книгу можно дать прочитать либо Дэвиду Копперфильду (решение А), либо Гарри Гудини (В), либо никому (С).
Предположим, что Гарри Гудини нравится такое чтение, и он предпочитает читать само произведение, а не избавляться от него (B>C). Однако еще большее удовольствие он получил бы от того, что Дэвид Копперфильд должен был прочитать эту книгу и немного поумнел (A>B>C).
Дэвид Копперфильд считает, что книга неприлична и ее вообще не следовало издавать, т.е. её вообще не стоит читать (он предпочитает, прежде всего, решение C). Однако, если кто-то должен это прочитать, Дэвид Копперфильд предпочел бы, чтобы это всё-таки сделал он, а не Гарри Гудини (A>B). Итак, для Дэвида Копперфилда C>A>B.
Учитывая предпочтения двух индивидуумов в обществе, специалист по социальному планированию должен решить, что делать. Должен ли планировщик заставлять Гарри Гудини читать книгу (A), заставлять Дэвида Копперфилда (B) читать её или оставить её непрочитанной (C)? Точнее, должен ли он ранжировать три возможных исхода в соответствии с их социальной желательностью?
Либеральный социальный планировщик решает, что он должен отстаивать права личности, каждый человек должен иметь возможность самостоятельно прочитать книгу.
Гарри Гудини должен иметь возможность решить, будет ли результат «Гарри Гудини читает» (B) иметь более высокий рейтинг, чем «Никто не читает» (C). Точно так же Дэвид Копперфильд также должен иметь возможность решить, будет ли результат «Дэвид Копперфильд читает» (A) выше, чем «Никто не читает» (C).
Следуя этой стратегии, социальный планировщик объявляет, что результат «Гарри Гудини читает» будет иметь более высокий рейтинг, чем «Никто не читает» (из-за предпочтений Гарри Гудини: B>C), и что «Никто не читает» будет иметь более высокий рейтинг, чем «Дэвид Копперфилд читает» (из-за предпочтений Дэвида Копперфилда в C>A). Затем согласованность требует, чтобы «Гарри Гудини читает» был выше, чем «Дэвид Копперфильд читает», и поэтому социальный планировщик дает Гарри Гудини книгу для чтения по принципу транзитивности B>C>A.
Но этот результат либерального планировщика, отдающего предпочтение индивидуальному выбору, и Дэвид Копперфильд, и Гарри Гудини считают хуже, чем «Дэвид Копперфильд читает» (А).
Действительно, Дэвид Копперфильд предпочитает читать плохую книгу вместо Гарри Гудини (A>B для Дэвида Копперфильда), а Гарри Гудини считает, что книга настолько хороша, что Дэвид Копперфильд обязательно должен ее прочитать (A>B также для Гарри Гудини).
Таким образом, результат, выбранный либеральным планировщиком, хуже по Парето. Есть еще один результат, который выше по Парето: тот, где Дэвид Копперфильд вынужден читать книгу.