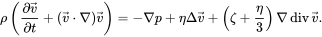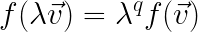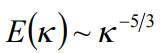Метод размерностей. Часть вторая
Снова всем привет! Я не ожидал, что так много людей подпишутся. Спасибо, друзья!
Как и обещал, вторая (математическая) часть про метод размерностей.
В первой части мы приписывали неким величинам некие размерности типа килограммов.
А сейчас мы сделаем примерно то же самое, но вместо размерностей будут обычные числа - масштабные коэффициенты.
Практически все инженеры пользовались или пользуются одной из реализаций этого метода, чтобы оценить работоспособность конструкции.
Я говорю, конечно, про закон квадрата-куба.
Звучит он так: если растянуть все линейные размеры тела в N раз, то его площадь вырастет в N^2 раз, а объем - в N^3 раз.
Вроде очевидно, но выводы из него получаются словно из рога изобилия!
Это связано с тем, что в природе есть эффекты, связанные с площадью тел, и есть эффекты, связанные с объемом тел.
Например, скорость остывания тела зависит от его площади поверхности. Чем больше площадь, тем быстрее тело остывает. Поэтому радиаторы делают со множеством пластин.
Увеличив линейные размеры в N раз, увеличим площадь в N^2, и тем самым ускорим остывание, но при этом масса радиатора увеличится в N^3 раз, что уже не так хорошо.
Или обратный пример: остывание воды. Как думаете, почему в ресторанах подают чай в чайниках, а не разлитый по кружкам? Площадь поверхности жидкости в чайнике меньше площади поверхности жидкости, разлитой по кружкам.Можете даже эксперимент дома провести: вскипятить 2 чайника, один разлить по 10 кружкам (даже накрыв их сверху чем-нибудь), а второй оставить так. И замерить температуру через 10 минут. Я утверждаю, что кружки будут холоднее чайника, который не разливался.
Чур не использовать кружки-термосы:)
В термосах есть дополнительная воздушная прослойка, из-за которой эффективная площадь теплового контакта будет не больше, а наоборот меньше.
С объемными эффектами дела обстоят похоже. Возьмем тот же чайник, и второй с линейными размерами в 2 раза бОльшими. По закону квадрата-куба во второй чайник поместится в 8 раз больше воды, чем в первый. Значит, при той же мощности нагревательного элемента он будет вскипать в 4 раза дольше, чем первый и потребует в 8 раз больше энергии.
Почему в 4 раза больше, а не в 8? Потому что нагревательный элемент тоже увеличился в размерах. Из-за этого его сопротивление стало вдвое меньше (R=rho*2*l/4S=R0/2), а выделяемая на нем мощность увеличилась вдвое (P=U^2/R=2*U^2/R0).
Это как раз причины, почему в общепите используют бойлеры, а не несколько маленьких чайников: бойлер медленнее остывает, тем самым экономит энергию, при этом время нагревания не так критично, как для домашних чайников.
Примеров применения закона квадрата-куба довольно много и с ними можете подробнее ознакомиться в Википедии (https://ru.wikipedia.org/wiki/Закон_квадрата_—_куба).
Я же вернусь к изначальной мысли сего поста. В предыдущем примере мы масштабировали тела - увеличивали все размеры в N раз.
Абсолютно тот же подход используется в теоретической физике, когда надо определить основные закономерности, а константы, которые будут получаться всегда можно забить в комп считаться. К тому же в экспериментах чаще всего проверяется не конкретное значение какой-то переменной или константы, а верна ли заявленная закономерность в целом.
Я не говорю сейчас про измерение постоянной Планка и других констант. Я больше про сами законы физики. При любом эксперименте, как и при описании этого эксперимента, важно понимать, что на самом деле мы мерим, какой результат мы хотим получить.
Например, есть уравнение Навье-Стокса, которое по сей день не имеет точного решения (вроде институт Клэя до сих пор не отдал никому награду за решение), но это не мешает нам его анализировать.
Страшно выглядит, не так ли?) Не бойтесь - оно здесь только для примера того, с чем приходится сталкиваться.
Тут важно правильно задать вопрос "А что вообще нас интересует?".
Как видно, уравнение Навье-Стокса накладывает ограничение на скорости потоков жидкости.
Но надо ли нам знать точно скорость каждой точки жидкости? Скорее всего, нет. Не так много задач, где именно это нужно узнать.
К тому же на него очень сильно влияют начальные и граничные условия. Уравнение одинаково применимо как для описания цунами, так и для помешивания чая, но результаты абсолютно разные именно из-за начальных и граничных условий.
Гораздо чаще нужно описать какое-то коллективное явление частиц жидкости.
А раз оно коллективное, то возможны 2 варианта:
1) не всё в уравнении Навье-Стокса нам важно. Чем-то можно пренебречь и значительно упростить себе работу. Так, например, появилась бабочка Лоренца и описание поверхностных течений.
2) мы будем мерить характеристики, общие для всего объема жидкости в заданных условиях.
К этому случаю относится описание развитой турбулентности. Например, удалось вычислить спектр энергий турбулентных вихрей, или простыми словами - зависимость энергии вихря от его размера. Тут важно, что уравнение Навье-Стокса не решалось явно, а только использовалось при выводе спектра энергий. Не в нем самом надо пробовать растягивать переменные, а в его следствиях.
Развитая турбулентность выглядит вот так
Так в чем же здесь заключается метод размерностей?
Если во всех используемых формулах растянуть в N раз координаты, сделать необходимые замены, то уравнения должны остаться прежними. При этом результат должен зависеть от какой-то комбинации растянутых параметров, а сам масштаб должен всюду сократиться. В этом смысле нас интересуют масштабные инварианты - комбинации переменных, которые не меняются при изменении масштаба рассмотрения процесса.
На языке математики величины в таких зависимостях от масштаба выглядит так:
Это уравнение на так называемые однородные функции, которые исследовались еще со времен Эйлера. Здесь уже q называется размерностью, а не килограммы и метры как в случае физического метода размерностей. При помощи этих соображений как раз можно вычислить спектр энергий турбулентных вихрей, несмотря на всю сложность уравнения Навье-Стокса, с которого начиналась задача. Кстати, вот он (спасибо Колмогорову за это):
Очевидно, что площадь и объем также являются однородными функциями линейных размеров. Поэтому закон квадрата-куба является частным случаем метода растяжений или размерностей. Может, я немного ошибся с названием "метода размерностей", но общая суть у всех его вариаций одна. На самом деле, его по-разному называют в разных областях науки - и аномальным скейлингом, и критическим скейлингом, и законом квадрата-куба. Смысл же довольно прост: давайте всё растянем да посмотрим, что изменится. Иногда хочется, чтобы ничего не изменялось, а иногда - наоборот.
На этом у меня всё:) Следующей темой будут законы сохранения. Напоследок сёрфера и воды вам в ленту.
P.S.: Опять же - конструктивная критика приветствуется.