Excel. Долгая дорога оцифровки. Часть 1. Немного теории⁠⁠

Итак, как и обещал, начинаю долгую серию постов посвящённую вопросам:

1. У меня есть точечно заданная функция (набор значений X Y), как найти значения между заданных точек?

2. У меня есть диаграмма в виде картинки, как превратить её в функцию Excel?

3. Как имея оцифрованную функцию отобразить поиск решения на диаграмме?

4. Как написать макрос создающий макросы оцифровки точечно заданных функций?

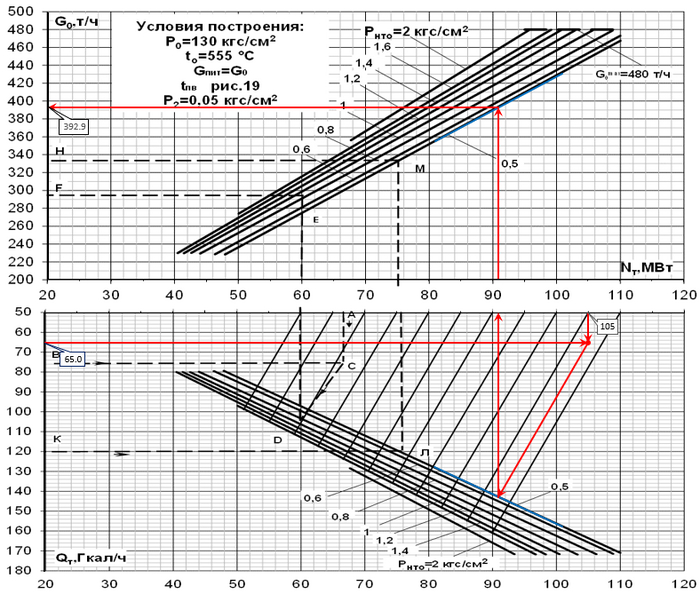
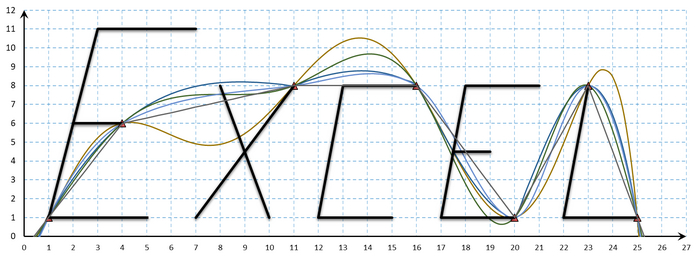
Как итог - получение автоматического расчёта и построения поиска для диаграмм вида:

Данная серия не будет нести развлекательной функции. Для кого то она покажется нудной, поскольку однозначного ответа "нажми на кнопку "сделать всё хорошо"" тут не будет.

Если кто в курсе темы - рад за Вас. Если что будет по теме - с радостью приму к сведенью.

Если кому то не интересно/не нужно - проходите мимо, ресурс позволяет найти инфу на любой вкус и настрой.

Итак, начнём. Немного теории...

Тема 1. Точка Шрёдингера.

Из определений в упрощённом виде, применительно к нашим работам:

Аппроксимация – под аппроксимационной кривой подразумевается некий полином (в нашем случае), коэффициенты которого подобраны так, что график построенный по этому уравнению проходит наиболее близко к известным точкам. При этом в известных значениях значения функции не обязательно совпадают с заданными значениями (в общем случае f(Xi) ≠ Yi).

Интерполяция – нахождение неизвестных промежуточных значений некоторой функции, по имеющемуся дискретному набору ее известных значений определенным способом. При этом в известных значениях значения функции совпадают с заданными значениями. Под интерполяционной кривой подразумевается некий полином (в нашем случае), график которого проходит через все известные точки.

Две особенности интерполяции:

- для получения полинома степени «n» требуется «n+1» заданная точка (например, полином первой степени f(x)=a·x+b требует две известные точки, или проще – линия строится по двум точкам, парабола по трём и т.д.);

- применение интерполяции методом «ближайшего соседа» (он же "округление"), и аналогичных, в нашем случае не применяется.

Экстраполяция – особый тип аппроксимации, при котором функция аппроксимируется вне заданного интервала, а не между заданными значениями.

На практике же имеется следующее: есть некая точечно (не путать с «точно») заданная зависимость, и требуется определить значение между заданных точек (для аппроксимации или интерполяции). Например, есть заданные значения при значениях аргумента 0, 1, 2…9, а узнать надо при 0.5 и 8.5.

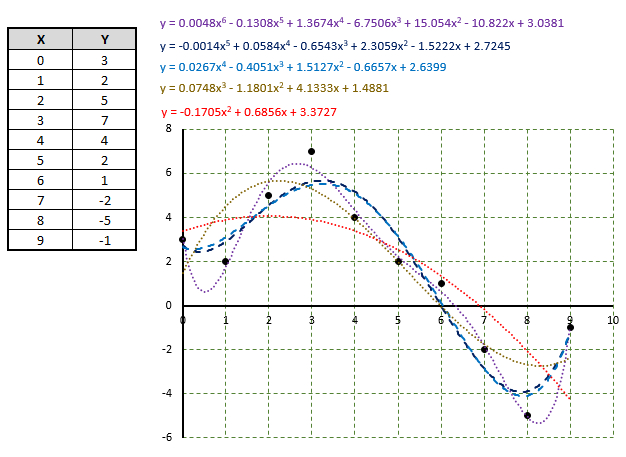
Попробуем найти полином с использованием линии тренда:

Как видно, в данном случае ни один из существующих полиномов линии тренда Excel не даёт интерполяционной кривой (проходящей через все точки), а наша цель:

- совпадение значений используемой функции значениям в реперных (заданных изначально) точках;

- совпадение или близость тенденции изменения параметров, т.е. в данном примере между т.1 и т.2 функция должна иметь постоянно уменьшающееся значение (при росте Х), а не как для полинома 6-й степени: для значений менее 0,5 - уменьшение, а от 0,5 до 1 - значительное возрастание.

Одним из вариантов решения является применение кусочной интерполяции, т.е. разбиения известного количества заданных точек на несколько групп с малым количеством точек таким образом, чтобы:

1) искомое значение Х содержалось в выбранном диапазоне;

2) для выбранного количества точек можно было найти функцию, график которой будет проходить через все выбранные точки.

Рассмотрим примеры кусочной интерполяции полиномом 1-й и 2-й степени.

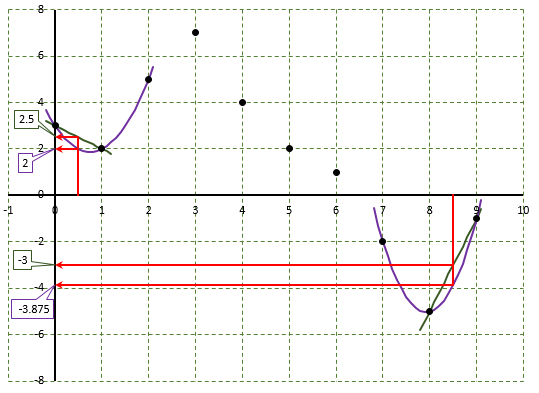
Для нашего примера для определения значения функции:

- при Х=0,5 при линейной интерполяции для построения полинома используются 1-я и 2-я точки, а для интерполяции полиномом второй степени  используются 1-я 2-я и 3-я точки;

- при Х=8,5 при линейной интерполяции для построения полинома  используются 9-я и 10-я точки, а для интерполяции полиномом второй степени используются 8-я 9-я и 10-я точки.

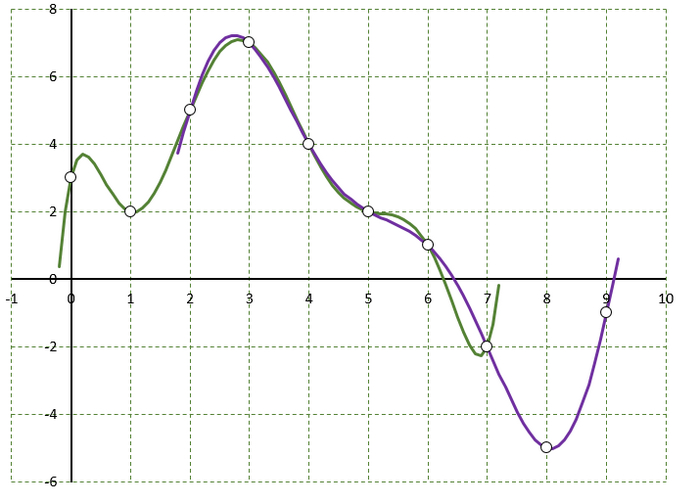
Как видно из рисунка ниже, результат зависит от используемого метода интерполяции как внутри заданных значений, так и, в значительной мере, при экстраполяции (для Х < 0 и > 9).

Возможно использование и полиномов более высоких степеней, но как правило, достаточно полинома первого/второго порядка, т.к. зависимости далеко не всегда являются полиномными.

При поиске решения с применением полиномов 2-й и более степеней следует понимать, что в зависимости от выбранных точек результат будет разным.

Например, при выборе полинома второй степени и поиске значений при Х=1,5 данные, полученные по полиному, построенному точкам х=1 – 2 – 3 (синяя линия), будут значительно отличаться от данных, полученных по полиному, построенному по точкам х=0 – 1 – 2 (фиолетовая линия). И так для большинства вариантов. В приведённом примере только на участке 4-5 есть совпадение кривых.

Аналогичные проблемы будут и при использовании полиномов более высоких порядков. Например, для анализируемого случая строятся графики с использованием полиномов 7-го порядка (а·х^7 + …), включающие первые и последние заданные точки. Первый интерполяционный график построен по точкам: х1-2-3-4-5-6-7-8, второй – по х3 4 5 6 7 8 9 10. Наличие сильных расхождений в зоне пересечения (между точками х3-4-5-6-7-8) очевидно, но главную проблему представляет собой поведение 1-го инт.графика в зонах х=0..1 и х=6..7.

В условиях ограниченности исходных полиномы высоких порядков могут принести необоснованную погрешность расчёта. А для некоторых вариантов применение отличного от кусочного метода интерполяции просто невозможно.

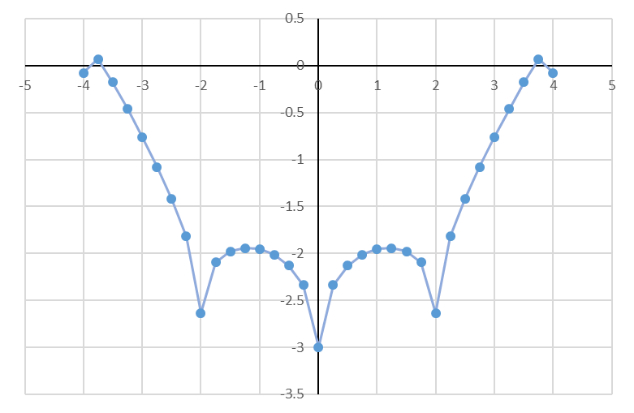
Например, есть точки графика функции полинома 9-й степени. Провести интерполяцию данных штатными средствами Excel невозможно (ограничение определения полинома Excel – 7-я степень). Кусочно-заданная функция потребует разбиение на несколько участков (более 3-х), и всё равно приведёт к значительным погрешностям даже в реперных точках. Либо у полученного графика будут аналогичные проблемы поиска данных в промежуточных точках:

Вывод – Не существует 100% достоверного математического способа определения промежуточных значений точечно заданной функции, за исключением частных вариантов или известных дополнительных зависимостей поведения функции.

Принимая решение о виде интерполяции надо понимать все риски и дополнительно понимать условия налагаемые на метод поиска решения.

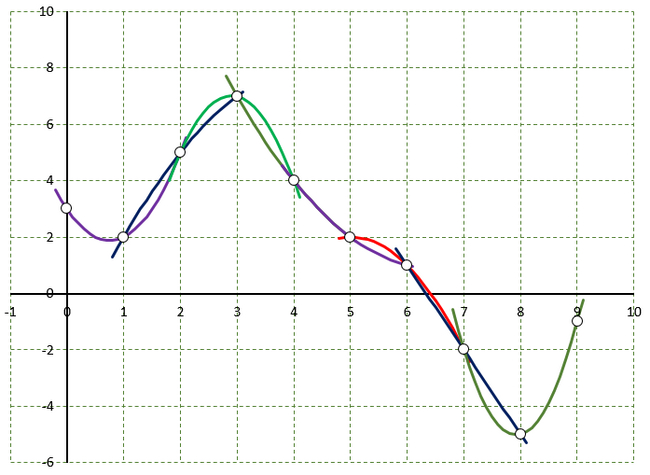
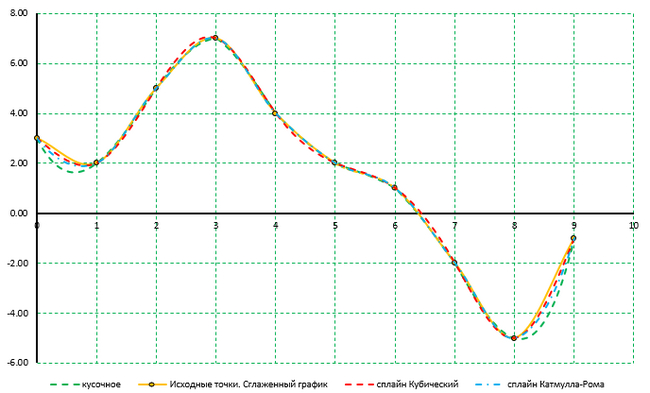
В качестве примера можно обратиться к графику ниже. На нём представлены 5 интреполяционных кривых, построенных по одним и тем же исходным точкам. Различие результатов между заданных точек более чем наглядно.

Так же стоит отметить наличие ошибки расчётов величин с плавающей запятой (вещественных). Подробнее с действующим стандартом можно ознакомиться по адресу https://www.softelectro.ru/ieee754.html

Далее небольшая выдержка с вышеуказанного сайта

Стандарт IEEE 754 широко применяется в технике и программировании.

Большинство современных микропроцессоров изготовляются с аппаратной реализацией представления вещественных переменных в формате IEEE754.

Язык программирования и программист не могут изменить эту ситуацию, иного преставления вещественного числа в микропроцессоре не существует.

Когда создавали стандарт IEEE754-1985 представление вещественной переменной в виде 4 или 8 байт казалось очень большой величиной, так как объём оперативной памяти MS-DOS был равен 1 Мб. А, программа в этой системе могла использовать только 0,64 Мб. Для современных ОС размер в 8 байт является ничтожным, тем не менее переменные в большинстве микропроцессоров продолжают представлять в формате IEEE754-1985.(с)

Вот как то так...Немного теории для понимания почему в дальнейшем применял какие то решения.

И да, применять/описывать сплайны не буду. :) Хотя надо знать, что Excel при построении сглаженного графика использует что то похожее на сплайн Катмулла-Рома (кроме 1 и последнего участков).

to be continued... (?)