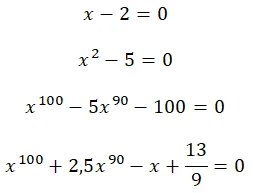Белые воротнички в мире математики - трансцендентные числа⁠⁠

Итак все Вы слышали про натуральные, рациональные и целые числа. Кроме того, немного вспомнив курс школьной математики на ум придут иррациональные и, может быть, комплексные. Но есть в царстве чисел особые объекты, уверяю, до боли Вам знакомые, выделяющиеся среди своих собратьев - это трансцендентные числа, о которых и поговорим в этой статье. Поехали!

Что за слово - трансцендентность?

Слово происходит от латинского transcendere — переходить, превосходить. И это действительно подходящее название. По отношению ко всем другим числам трансцендентные являются "белыми воротничками".

Дело в том, что остальные числа вовсе не чураются быть корнями алгебраических уравнений, в то время как трансцендентные в уравнения силком не затащишь.

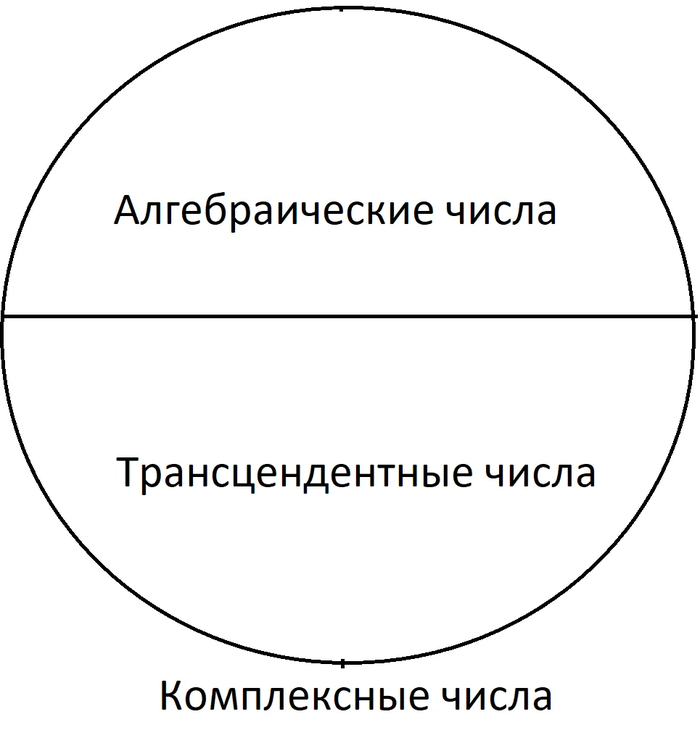
Комплексные числа (которые вида x+iy, где i - мнимая единица) делятся на два непересекающихся класса чисел: алгебраические (могут быть корнями алгебраических уравнений) и трансцендентные. Что такое алгебраическое уравнение? Вот примеры:

Если кратко, то к алгебраическим уравнения можно отнести те уравнения, коэффициентами при неизвестных которых являются любые целые или рациональные числа.

Каждое из вещественных трансцендентным чисел является иррациональным, а вот обратное неверно. Например,

Кроме того, известно, что если сложить два трансцендентных числа, умножить, извлечь корень или возвести в натуральную степень, результат будет трансцендентным.

Так какие числа трансцендентны?

Как и обещал, почти каждому из Вас знакомы эти товарищи:

число пи = 3,1415;
число Эйлера е = 2,71828, которое появляется во втором замечательном пределе;
постоянная Гельфонда, равная е в степени пи;
десятичный логарифм любого натурального числа, естественно, кроме 10 в степени n (тогда этот логарифм по определению равен n);
синус, косинус и тангенс любого ненулевого алгебраического числа.

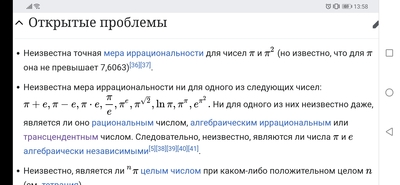
С трансцендентными числами связана одна из 23 математических проблем (7-ая по счету), сформулированных великим Давидом Гильбертом (который, кстати, жил и творил на территории современной России):

Эту проблему решил в 1934 советский математик Александр Осипович Гельфонд, доказав трансцендентность таких чисел.

Еще один интересный факт состоит в том, что несмотря на кажущуюся малочисленность трансцендентных чисел гораздо больше, чем алгебраических. Вы воскликните: "Но как одних чисел может быть больше, чем других, ведь и тех и тех - бесконечность!?".

Ответы на этот и другие вопросы в телеграмм-канале - Математика не для всех