Геометрия, раскрой, объем
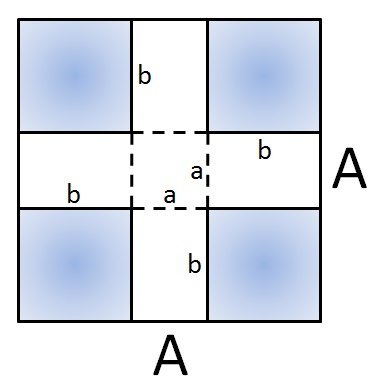
Представьте себе, что у Вас есть лист алюминия размером АхА (как показано на рисунке) и Вы решили сделать из него емкость (ну скажем - ведро) в виде четырехгранной призмы с квадратным основанием "аха" и высотой граней "b". При этом, раскрой листа вы решили делать абсолютно симметрично, исключая закрашенные, квадратные части (см. рисунок) с дальнейшим, встречным сгибанием граней призмы по пунктирной линии. Дальше Вы берете сварочный аппарат и свариваете все совмещенные ребра призмы. И вот наша емкость готова!
Вы несете Ваше, новоиспеченное ведро своему соседу, чтобы похвастаться. И тут Вы узнаете, что Ваш сосед тоже сделал ведро из такого же листа алюминия (АхА) и по такому же принципу. И когда Вы решили сравнить чье ведро лучше, выяснилось, что у Вашего соседа ведро получилось на 5 литров больше, так как он выбрал другое соотношение параметров "а" и "b".
Горькое поражение! Вы возвращаетесь домой с опущенной головой и думаете лишь о том как так могло получиться и то, что Вы поспешили резать лист алюминия, не подумав о качестве конечного результата и то, что израсходовали площадь листа не оптимально. Будучи дома Вы взяли лист бумаги, достали из шкафа пыльную ручку и начали думать, как можно заранее вычислить оптимальные значения параметров (площади основания и высоты) Вашего будущего ведра, применив которые Вы бы получили максимальный объем.
Предложите метод предварительного вычисления параметров призмы (a и b) с целью получения ее максимального объема и рассчитайте максимально возможный объем призмы, если бы она делалась (описанным способом) из листа размером 90х90 (см) (АхА)!