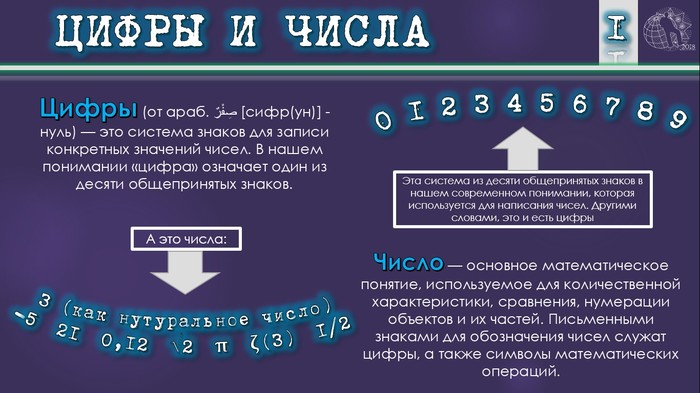
Развеиваем мифы о "современных цифрах".
Настолько надоело слышать и читать все эти вымыслы про наши "арабские" цифры, что решил сделать "слайд-пост" про них. Но для начала разберёмся с терминами "цифра" и "число", а то многие и это путают 😣 Читаем, запоминаем и распространяем!
------------------
Источники:
1. Florian Cajori. A History of Mathematical Notations / Vol I: Notations In Elementary Mathematics. New York, 2007. - 472 p.
2. http://www-history.mcs.st-andrews.ac.uk/HistTopics/Arabic_nu...
3. https://en.wikipedia.org/wiki/Arabic_numerals
4. http://nikitaefremov.ru/2015/07/08/1339/
5. https://ru.wikipedia.org/wiki/%D0%A6%D0%B8%D1%84%D1%80%D1%8B