Ответ на пост «И вновь начался срач»⁠⁠1

Пользователь @MIXAB написал такой комментарий #comment_309359607

Не буду спорить насчет удобства записи, а лишь прокомментирую следующую ветку:

Ответ на пост «И вновь начался срач» Математика, Теорема Пифагора, Квадратный корень, Из сети, Срач, Геометрия, Скриншот, Ответ на пост, Комментарии на Пикабу

Проблема возникает из-за того, что запись xⁿ означает сразу три функции.

Во-первых, есть чисто алгебраическая операция, которая определена на любом кольце и обозначает многократное повторение умножения, то есть хⁿ=х...х - умножение n раз. В случае если х обратим и корректно писать х⁻¹, то можно писать и х⁻ⁿ=(х⁻¹)ⁿ. Это хорошая, корректная операция. В случае с вещественными числа целые степени определены для любого ненулевого числа, натуральные - для вообще всех.

Во-вторых, есть функция f(x)=xⁿ, которая имеет смысл в вещественных числах, и которая любому неотрицательному числу единственным образом возвращает единственное неотрицательное число. Данная функция определяется через пределы рациональных степеней. Как правило именно эту функцию и обозначают радикалом в школе.

Но есть небольшой нюанс, если степень вида 1/n, где n - нечетное, то такие корни можно извлекать и из отрицательных вещественных чисел. И это тоже будет однозначной функцией. Поэтому, иногда, разрешают писать ∛(-3).

И последняя, это многозначная функция f(x)=xⁿ, которая записывается уже в комплексных числах, и которая устроена сильно хитрее и функцией, вообще говоря, не является. Точнее, функцией она становится на поверхностях Римана, если мне память не изменяет. Здесь и показатель, и основание можно выбирать любым, кроме случая 0⁰. Для изучения этой многолистной хрени лучше почитать книжки по ТФКП.

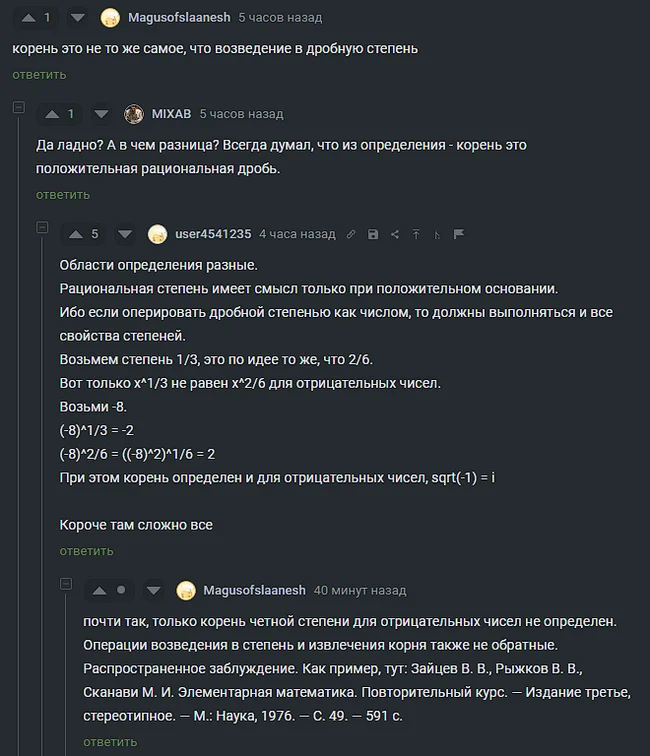
Скриншоты комментов

57.5K постов40.4K подписчиков

Добавить пост

Правила сообщества

В сообществе можно размещать ЛЮБЫЕ скрины (комментов) с любого сайта!!

ПРИКРЕПИТЬ ССЫЛКУ НА КОМЕНТ ЕСЛИ ОН С Пикабу желательно, но не обязательно!!!

Если скрин не с пикабу, а со стороннего сайта( Твиттер,. Вк, Одноклассники и т.д.) то ссылка не обязательна.

Для сообщества подходит любой скрин, набранный на клавиатуре, даже если это не диалог (под вид Твита) Так же подходит скрин с картинкой и хотя бы одним комментарием под ним, с любого источника.

1 пост-ответ

от Kenjity

Смотреть

venanen

3 месяца назад

Какое-то рассуждение о насущном, а не разделы математики, это больше удел философов.
Есть операция вида x^n - это просто возведение в степень. В степень можно возвести что угодно и когда угодно, разложив это в ряд умножения, а ряд умножения в ряд сложения.
Есть функция f(x, n) = x^n, которая возвращает всегда одинаковый результат, без домыслов. И в случае n<0 и n%2 = 0 - результатов будет два, мы берём тот, который нам нужен сейчас. Или можем взять оба.
Это как в школьной математике, где в задаче считается какая-нибуть скорость из квадратного уровня с одним положительным, другим отрицательным корнем, нас учили брать положительный ответ, хотя отрицательный тоже вполне может существовать

раскрыть ветку (1)

Kenjity

3 месяца назад

Какое-то рассуждение о насущном, а не разделы математики, это больше удел философов.

Да, это раздел, где люди договариваются о понятиях, а не получают результаты, то есть это раздел скорей философии науки, чем науки как таковой.

Есть операция вида x^n - это просто возведение в степень. В степень можно возвести что угодно и когда угодно, разложив это в ряд умножения, а ряд умножения в ряд сложения.

Увы, но это работает только для натуральных степеней. Попытка определить, например, что такое 2^(sqrt(3)+i) таким образом обречена на провал.

Есть функция f(x, n) = x^n, которая возвращает всегда одинаковый результат, без домыслов. И в случае n<0 и n%2 = 0 - результатов будет два, мы берём тот, который нам нужен сейчас. Или можем взять оба.

Если мы берем оба, то это уже получается двузначная функция. И если в вещественных числа, извлекая квадратный корень можно договорится брать положительный результат, то извлекая, например, корень из чисел отрицательных или комплексных, вообще говоря, не понятно как выбрать одну ветвь.

Это как в школьной математике, где в задаче считается какая-нибуть скорость из квадратного уровня с одним положительным, другим отрицательным корнем, нас учили брать положительный ответ, хотя отрицательный тоже вполне может существовать

Все верно. В школьной математике нужна именно такая функция. Это та, которую я упомянул второй в своем посте. В школе детей знакомят с вещественным анализом, учат решать физические задачи. Я думаю, если бы им начали читать полноценный комплексный анализ, были бы большие проблемы.

Собственно, все, про что я написал, это не мной придумано. Это нормальное развитие математики. А именно, показательная функция очень полезна, но попытки как-то определить её для комплексных чисел сталкиваются с известными трудностями. Например, то выражение, что я выше написал. Поэтому придумывают всякие штуки типа главного значения, поверхностей Римана.