Нерешаемое уравнение
Подрабатываю репетитором.
На прошлом занятии мальчик пришел и рассказал, как учитель назвал схему Горнера* полной хренью и чтоб мальчик так больше не решал. Я удивился, придумал уравнение, попросил дать учителю, чтобы тот предложил метод решения. Знаете, что ответил учитель? "Это уравнение не решается". Негодую. Вот то уравнение с решением.
Мне искренне непонятно - как такой человек может объяснять олимпиадные задания, сложные задачи ЕГЭ? Вот как?..
* Схема Горнера позволяет решать уравнения 3, 4, 5 и т.д. порядка, если можно подобрать корень. Тогда по этой схеме можно понизить степень. То есть, было кубическое, стало квадратным и решается на ура. Да, есть много других методов.
Плюсы: достаточная простота решения сложных уравнений (и вообще возможность их решить).
Минусы: иногда сложно подобрать корень; если уравнение выше 5 степени, то использование схемы Горнера становится совсем нерациональным.
https://math1.ru/education/raznoe/gorner.html


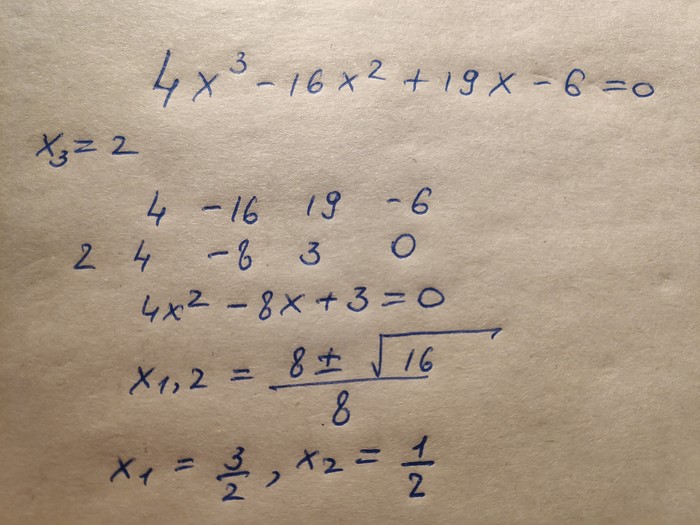
Лига образования
5.2K поста22.2K подписчиков
Правила сообщества
Публиковать могут пользователи с любым рейтингом. Однако мы хотим, чтобы соблюдались следующие условия:
ДЛЯ АВТОРОВ:
Приветствуются:
-уважение к читателю и открытость
-желание учиться
Не рекомендуются:
-публикация недостоверной информации
ДЛЯ ЧИТАТЕЛЕЙ:
Приветствуются:
-конструктивные дискуссии на тему постов
Не рекомендуются:
-личные оскорбления и провокации
-неподкрепленные фактами утверждения
В этом сообществе мы все союзники - мы все хотим учиться! :)